数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学
已知：圆的周长和半径之差 = 37 厘米
求解：求圆的周长 (厘米)
解：设给定圆的半径为 r。
∴ 圆的周长 = 2πr = 2 × 22/7 × r
圆的周长和半径之差 = 2 × 22/7 × r - r = 37r/7
已知，圆的周长和半径之差为 37 厘米，比较可得，
37r/7 = 37
⇒ r = 7 厘米
∴ 给定圆的周长 = 2πr = 2 × 22/7 × 7 ... 阅读更多
已知：等差数列 1/(3q), (1-6q)/(3q), (1-12q)/(3q), ......
求解：求给定等差数列的公差
解：给定的等差数列为：
1/(3q), (1-6q)/(3q), (1-12q)/(3q), ......
已知，公差 = 两个连续项的差 = (1-6q)/(3q) - 1/(3q) = (1-6q-1)/(3q) = -6q/(3q) = -2
∴ 选项 (C) 正确。
已知：外切于圆的平行四边形。 求证：外切于圆的平行四边形是菱形。
解：∵ 给定平行四边形 ABCD 外切于圆，其边在点 P、Q、R 和 S 与圆相切。
∴ AP 和 AS 是从外点 A 引出的圆的切线。BP 和 BQ 是从外点 B 引出的圆的切线。CQ 和 CR 是从外点 C 引出的圆的切线。DR 和 DS 是从外点 D 引出的圆的切线。
我们知道，从外点引出的圆的切线…… 阅读更多
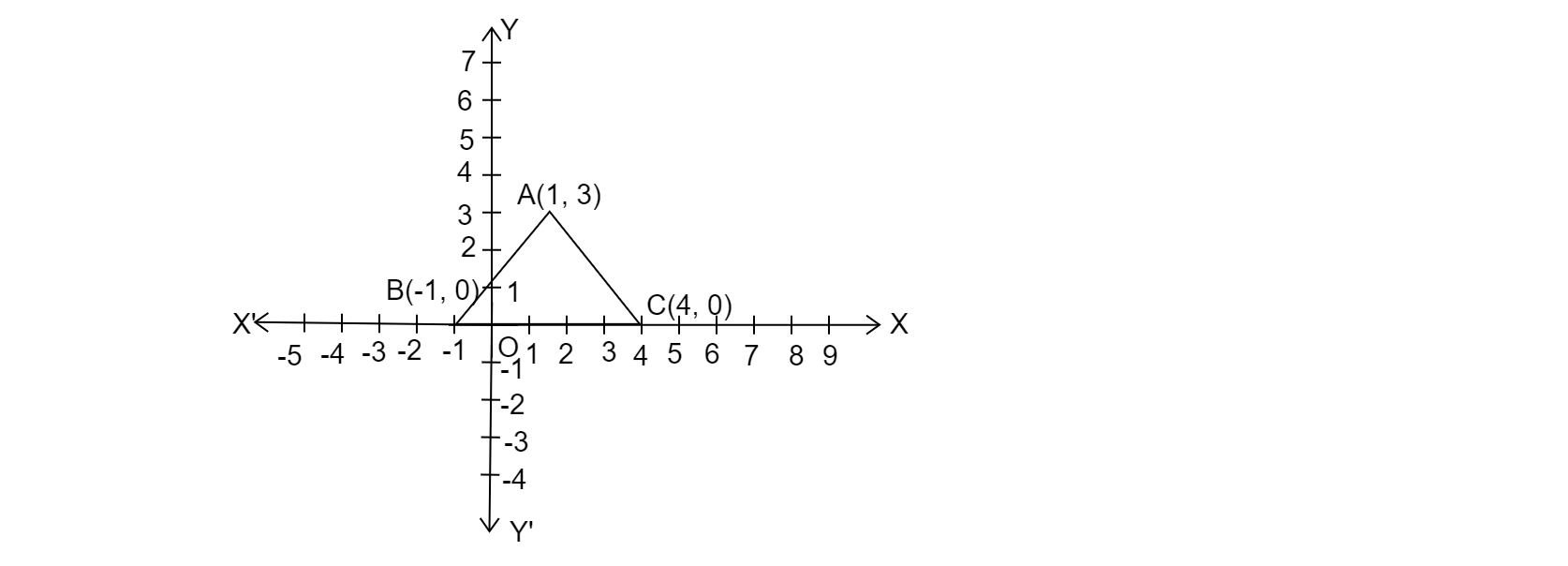
已知：图中三个顶点 A、B 和 C。
求解：求三角形 ABC 的面积（平方单位）。
解：我们知道，顶点为 (x1, y1)、(x2, y2) 和 (x3, y3) 的三角形的面积为 1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
此处，如图所示，顶点 A(1, 3)、B(-1, 0) 和 C(4, 0)
∴ 三角形 ABC 的面积 = 1/2[1(0-0) -1(0-3) + 4(3-0)] = 1/2(0+3+12) = 15/2 = 7.5 平方单位
∴ 选项 (C) 正确。
已知：半径为 4 厘米的圆，以及从外点 P 引出的圆的两条切线 PA 和 PB。并且 PA⊥PB
求解：求切线 PA 和 PB 的长度。
解：已知，PA 和 PB 分别是点 A 和 B 处的圆的切线，从外点 P 引出。
∴ PA=PB，（从外点引出的圆的切线长度相等。）
∴ CA⊥PA 和 CB⊥PB
∵ 半径总是垂直于接触点的切线。
并且 PA⊥PB（已知…… 阅读更多
已知：掷一次骰子。
求解：求掷骰子时得到偶数的概率。
解：掷骰子时，
共有可能的结局 (1,2,3,4,5,6) = 6
有利结局的数量 (2, 4, 6) = 3
有利结局的概率 = 有利结局的数量 / 总可能结局的数量 = 3/6 = 1/2
因此，掷一次骰子得到偶数的概率是 1/2。
∴ 选项 (A) 正确。
已知：一个盒子里有 90 个圆盘，编号从 1 到 90。
求解：从盒子里抽取一个圆盘时，该圆盘上的数字小于 23 的质数的概率。
解：盒子里圆盘的数量 = 90
总可能结局 = {1, 2, 3, 4,.......90}
总可能结局数 = 90
小于 23 的质数为 {2, 3, 5, 7, 11, 13, 17, 19}
因此，有利结局数 = 8
得到质数编号圆盘的概率 = 有利结局数 / 总可能结局数 = 8/90 = 4/45
∴ 选项 (C) 正确。
已知：一个以 O 为中心的圆内接于四边形 ABCD，分别在 P、Q、R 和 S 与 AB、BC、CD 和 DA 相切。
求解：求圆的半径。
解：如图所示，四边形 ABCD 在 P、Q、R 和 S 与圆相切。因此，AR 和 AQ 分别是 R 和 Q 处的圆的切线。BP 和 BQ 分别是 P 和 Q 处的圆的切线。CP 和 CS 分别是 P 和 S 处的圆的切线。DR 和 DS 分别是 R…… 阅读更多
已知：塔顶到汽车的俯角 = 30°，塔高 = 75 米。 求：汽车到塔底的距离。 解：设塔 AC 为已知塔，B 为汽车，如图所示。 已知塔高 AC = 75 米，塔顶到汽车的俯角∠DAB = 30°， 因为 DA∥BC，所以∠DAB = ∠ABC = 30° tan30° = AC/BC = 75/BC ⇒ 1/√3 = 75/BC ⇒ BC = 75√3 选项 (C) 正确。 阅读更多
已知：h(t) = t² – 15 求：这里，我们要求 h(t) 的零点。 解：为了求 h(t) 的零点，我们必须令 h(t) = 0。 这意味着，t² – 15 = 0 t² – √(15)² = 0 (t + √15)(t – √15) = 0 (因为 a² - b² = (a + b)(a - b)) t + √15 = 0 且 t – √15 = 0 t = -√15 且 t = √15 因此，二次方程 h(t) = t² – 15 的零点为 -√15 和 √15。 验证：我们知道， 零点之和 = -t 的系数 / t² 的系数 = -0/1 (t 的系数为 0) = 0 零点之… 阅读更多