
第一章 - 认识数字
引言
几千年前,人们用手指计数到10。如果物体的数量超过10,他们使用记号。

伊尚戈骨
伊尚戈骨是在非洲刚果国发现的。这些骨头上刻有64道类似记号的划痕,用于记录数字。但这对于计数大数来说是不够的。
数字系统
苏美尔人和埃及人发展了自己的数字系统,但它们都有各自的问题。
苏美尔数字系统并不固定或标准化。每个城市都有自己不同的写数字的方式。
埃及人使用符号来表示数字。这些符号适合计数,但对于表示大数效率低下。
随着人类文明的发展,他们需要更先进的数字系统。
罗马数字系统
罗马数字系统在中世纪后期广泛用于欧洲。罗马数字至今仍在钟表和国王、君主、教皇的名字中使用,例如查理四世、教皇保罗二世、理查三世等等。
罗马数字系统中没有零。
印度-阿拉伯数字系统
目前,印度-阿拉伯数字系统在世界各地使用。该系统大约在公元7世纪在印度发展起来。
最初,它只有1到9的数字。零0这个数字是在后来由杰出的印度天文学家和数学家阿耶波多发明后添加的。
后来,意大利数学家莱昂纳多·斐波那契将这个系统引入了欧洲。
比较数字
数字的位值
数字中不同位置的数字具有不同的位值。
- 一位数只有一个个位。
- 两位数有十位和个位。
- 三位数有百位、十位和个位。
比较一组数字时,我们考虑最左边的数字,因为它的位值是该数字所有数字中最大的。
- 个位上的数字是1的倍数。
- 十位上的数字是10的倍数。
- 百位上的数字是100的倍数,以此类推。
示例
Question: Compare the numbers: 893 and 398. Solution: The number 893 has 8 hundreds, 9 tens, and 3 ones The number 398 has 3 hundreds, 9 tens, and 8 ones. 893 has more number of hundreds than 398. Hence, 893 > 398
可以使用以下规则比较一组数字。
规则1
计算每个数字的位数。
- 数字位数越多,数字越大。
- 但0在非零数字之前的例外情况除外。例如,数字00073只有两位数,因为前面的0被忽略了。
示例
Question: Identify the largest and the smallest numbers among 9785, 879, 94567, and 78. Solution: The number 94567 has 5 digits; it is the largest in the given list. The number 78 has only 2 digits; it is the smallest.
规则2
如果两个数字的位数相同,则比较给定数字的最左边的数字来确定哪个数字更大或更小。
示例
Question: Compare the numbers: 9867 and 2347. Solution: Both these numbers have the same number of digits, i.e., 4. They have 9 and 2 as their leftmost digits. Since 9 > 2, the number 9867 > 2347.
示例
Question: Compare the numbers: 531 and 764. Solution: Both the numbers have 3 digits each. The leftmost digits of the numbers are 5 and 7. Since 5 < 7, 531 < 764.
规则3
如果数字的位数相同且最左边的数字相同,则比较数字的下一个最左边的数字,并重复此过程。
示例
Question: Compare the numbers: 6791 and 6340 Solution: Both the numbers have the same number of digits, i.e., 4 each. The leftmost digits of the numbers are same, i.e., 6 So, we move to the next leftmost digit. The next leftmost digits of the numbers are 7 and 3. Since 7 > 3, 6791 > 6340
移动数字
给定一定数量的数字,可以通过移动和排列数字来形成许多新的数字。例如:
- 用3个不同的数字,可以形成6个不同的数字。
- 用4个不同的数字,可以形成24个不同的数字,以此类推。
示例
Question: Form as many new numbers as possible with the digits 1, 7, and 9.
Solution:
We can form 6 different numbers by shifting and shuffling the given digits.
The numbers are:
197, 179, 791, 719, 917, and 971
最大数和最小数
要从给定的数字中得到最大数,先写下最大的数字,然后在其右边写下第二大的数字,依此类推。
同样,要从给定的数字中得到最小数,先写下最小的数字,然后在其右边写下第二小的数字,依此类推。
升序和降序
如果我们将一组数字从小到大排列,则称为升序。
另一方面,如果数字从大到小排列,则称为降序。
示例
Question: Form new numbers using the digits 2, 3, and 5. Identify the largest
and the smallest numbers. Then, arrange the numbers in ascending
and descending orders.
Solution:
The numbers that can be formed using 2, 3, and 5 are:
235, 253, 352, 325, 523, and 532
The largest number in the list = 532
The smallest number in the list = 235
Arranging the numbers in ascending order:
235, 253, 325, 352, 523, 532
Arranging the numbers in descending order:
532, 523, 352, 325, 253, 235
阅读数字
在读写数字时,我们使用数字中数字的位值。
数字的展开式
数字的展开式是其所有数字乘以其位值的总和。
例如,数字15826可以展开为:
| 万位 | 千位 | 百位 | 十位 | 个位 |
| 1 | 5 | 8 | 2 | 6 |
15826 = 10000 + 5000 + 800 + 20 + 6
= (1 × 10000) + (5 × 1000) + (8 × 100) + (2 × 10) + (6 × 1)
示例:数字7893的展开式是什么?
解答
7893对应的位值是:
| 千位 | 百位 | 十位 | 个位 |
| 7 | 8 | 9 | 3 |
67893的展开式
| 7000 | 800 | 90 | 3 |
| 7 × 1000 | 8 × 100 | 9 × 10 | 3 × 1 |
示例
Question: Write and expand the number thirty-five thousand two hundred and sixty-nine.
Solution:
Thirty-five thousand two hundred and sixty-nine is = 35,269
35,269 = 30000 + 5000 + 200 + 60 + 9
= 3 × 10000 + 5 × 1000 + 2 × 100 + 6 × 10 + 9 × 1
展开式到标准形式
示例
Question: Write the standard form of the number from its expanded form, 8 × 10000 + 8 × 1000 + 6 × 100 + 1 × 10 + 9 × 1 Solution: 8 × 10000 + 8 × 1000 + 6 × 100 + 1 × 10 + 9 × 1 = 80,000 + 8000 + 600 + 10 + 9 = 88,619
记数系统
我们知道如何使用位值来读写数字;但是一遍又一遍地在数字上写位值不是一个好主意,尤其是在大数的情况下。
有一种更好的方法可以使用逗号来读写大数。
记数系统
有两种记数系统,即:
- 印度记数系统和
- 国际记数系统。
印度记数系统
在印度记数系统中,逗号用于分隔千位、十万位和千万位。在这个系统中:
- 第一个逗号放在百位之后,以标记千位;
- 第二个逗号放在左边接下来的两位数字之后,以标记十万位;
- 第三个逗号放在左边接下来的两位数字之后,以标记千万位。
示例
Question: Write the number 528792432 as per the Indian System of Numeration.
Solution:
Placing commas as per the Indian System of Numeration,
52,87,92,432
This number can be read as,
52 crores, 87 lakhs, 92 thousands and 432
国际记数系统
在这个系统中,有 个位、十位、百位、千位和百万位。在这里:
- 第一个逗号放在从右数的三个数字之后,以标记千位;
- 第二个逗号放在左边再三个数字之后,以标记百万位。
在这个系统中,逗号每隔三个数字从右往左放置。
示例
Question: Write the number 15862942 as per the International System of Numeration.
Solution:
Placing commas as per the International System of Numeration,
15,862,942
This number can be read as,
15 million, 862 thousands and 942
The number greater than a million is a billion and 1 billion = 1000 million.
The same number is represented differently in the two systems of numeration.
示例
Question: Represent the number 85122263 in both the Indian System of Numeration and the International System of Numeration.
Solution:
This number, when represented in the Indian system of numeration, is written as,
8,51,22,263
It's read as 8 crores, 51 lakhs, 22 thousand and 263.
The same number, in the International system of numeration is written as,
85,122,263
It's read as 85 million, 122 thousand and 263.
计量单位
我们有很多工具和仪器可用于以不同的单位测量长度、重量和体积等参数。这些仪器可以用来测量从小的种子到高大的山脉。
测量长度和距离
尺子或刻度尺用于在纸上画线。它有两种标记:
- 大标记表示厘米 (cm)。
- 小标记表示毫米 (mm)。
这两个单位都用于测量像铅笔一样又小又细的东西。
对于测量像房子一样较大的东西,使用卷尺,其标记为毫米、厘米和米 (m)。
米比厘米或毫米大得多。
1 m = 100 cm = 1000 mm
1 cm = 10 mm
还有更大的单位,如公里 (km)
1 km = 1000 m
测量质量或重量
为了测量重量,有像毫克 (mg)、克 (g) 和千克 (kg) 这样的单位。
克比毫克大。
1 g = 1000 mg
同样,1 kg 比克和毫克都大。
1 kg = 1000 g
测量体积
也有不同的单位来测量体积。例如,毫升、升和千升:
1 升 (l) = 1000 毫升 (ml)
1 千升 (kl) = 1000 升 (l)
需要注意的是,在所有测量中,无论是长度、重量还是体积,某些术语是通用的,如千、厘和毫。其中:
毫 < 厘 < 千
千是基本单位的1000倍
1 km = 1000 m;1 kg = 1000 g;1 kl = 1000 l
厘是基本单位的100分之一
100 cm = 1 m
毫是基本单位的千分之一
1000 mm = 1 m;1000 mg = 1 g;1000 ml = 1 l
理解估计
什么是估计?
估计或近似值意味着对某个数量或计算结果有一个大致的了解。作为估计给出的数字不是精确的数量,而是一个近似值,它可以很好地表示实际数字。
示例
通常说印度人口是13亿。这不是确切的数字,而是对人口的估计。
据估计,体育场内的观众人数约为10,000人。这意味着观众人数可能在9,500人左右或11,500人左右,而不是像50,000人这样的大数字。
四舍五入到十位
四舍五入到最接近的十位意味着将数字四舍五入到0、10、20、30等。
考虑数字13。它位于数轴上的10和20之间。在这两个数字中,13更接近10。所以13四舍五入到10。
52四舍五入到50,因为它更接近50。
78四舍五入到80,因为它更接近80。
5与0和10的距离相等。在这种情况下,一般规则是将中间值四舍五入到较大的数字。因此,5四舍五入到10。
四舍五入到百位
这意味着将给定数字四舍五入到0、100、200、300等。
示例
Question: Round off 528, 798, and 350 to their nearest hundreds. Solution: a) 528 is closer to 500; so it is rounded off to 500. b) 798 is closer to 800; so it is rounded off to 800. c) 350 is equidistant from 300 and 400. Applying general rule, it is rounded off to the larger value which is 400.
四舍五入到千位
将数字估计到最接近的千位意味着将它们估计到0、1000、2000、3000等。
- 考虑0到1000之间的数字。
- 数字2、3、4…499更接近0,因此四舍五入到0。
- 数字501、502…999更接近1000,因此四舍五入到1000。
- 500与0和1000的距离相等。根据一般规则,500四舍五入到较大的数字1000。
估计和与差
我们已经学习了如何将数字四舍五入。现在是时候学习如何在进行加法、减法和乘法运算时估计数字了。
示例
Question: A trader is to receive ₹13,569 from one source and₹26,785 from another.
He has to make a payment of ₹37,000 to someone else by the evening. Does the trader
have enough money for the day?
Solution:
Rounding off ₹13,569 to thousands = ₹14,000
Rounding off ₹26,785 to thousands = ₹27,000
The trader will get approximately,
₹14,000 + ₹27,000 = ₹41,000
He has to pay = ₹37,000
₹41,000 − ₹37,000 = ₹4000
The trader has enough money for the day.
示例
Question: Estimate the difference between two numbers, 5673 − 436.
Solution:
5,673 rounded off to thousands = 6,000
436 rounded off to thousands = 0
6000 − 0 = 6000
This is not a good estimate.
We can get a better estimate if the numbers are rounded off to the nearest hundreds.
5,673 rounded off to hundreds = 5,700
436 rounded off to hundreds = 400
5700 − 400 = 5300
So, the difference between 5673 and 436 is approximately 5300.
罗马数字
罗马数字起源于古罗马。与其他数字系统一样,罗马数字使用不同的符号来表示不同的数字。
事实上,罗马人使用拉丁字母中的7个符号来表示数字。
- "I" 用于表示1
- "V" 用于表示5
- "X" 用于表示10
- 同样,L = 50,C = 100,D = 500,M = 1000
任何数字都可以使用这7个符号来书写。但是,有一些规则需要遵守:
规则1
如果重复数字或符号,则其值将根据其出现的次数相加。例如:
- II 表示 1 + 1 = 2 (因为 I = 1)
- III 表示 1 + 1 + 1 = 3。
规则2
一个符号不能重复超过三次。
三个符号 V、L 和 D 永远不能重复。
规则3
如果较小值的符号写在另一个较大值符号的前面,则其值将从较大值符号中减去。例如:
- IV = 5 − 1 = 4
- IX = 10 − 1 = 9
根据此规则,不能在较高值符号之前写两个符号。例如:
IIV 是无效的数字。
IIV ≠ 3
III = 3
规则4
如果较小值的符号写在较大值符号的右边,则这两个值将相加。例如:
VI = 5 + 1 = 6
XI = 10 + 1 = 11
规则 5
符号 V、L 和 D 不能写在比其数值更大的符号的左边。这意味着 V、L 和 D 的值不能从比其数值更大的符号中减去。
此外,一个值不能从比其值大十倍以上的数值中减去。例如:
I 可以从 V 中减去,即 IV = 4
I 可以从 X 中减去,即 IX = 9
但是,I 不能从 XX 中减去。因此,IXX 是一个无效的罗马数字。
规则 6
要写出大于或等于 4000 的数字,IV、V、VI 要加上上划线。例如:
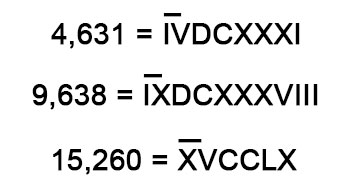
罗马数字的缺点
用罗马数字书写大数字并不容易。因此,它最终被印度-阿拉伯数字系统所取代。
罗马数字系统的另一个主要缺点是缺少相当于“0”的符号。