
第10章 - 测量
测量学导论
我们使用不同的单位来测量不同的东西。例如,为了测量时间,我们使用分钟、秒和小时。同样,为了测量距离,我们使用公里、米等。
事实上,有一个专门的分支叫做计量学,专门处理测量问题。
什么是测量学?
测量学是几何学的一部分,它涉及到对不同几何形状及其测量的研究。我们使用测量学来计算不同几何形状的长度、宽度、深度、面积和体积。
几何形状有两种类型:2D 和 3D。
2D 形状
2D 形状由三条或多条直线或平面上的封闭圆圈包围。它们有两个维度:长度和宽度,因此被称为 2D 图形或形状。对于 2D 形状,我们测量面积和周长。
2D 形状的例子包括圆形、矩形、正方形、三角形、梯形等。
3D 形状
3D 形状由多个平面包围。这些也被称为立体形状。
除了长度和宽度之外,3D 形状还有高度(或深度)。
一些众所周知的 3D 形状:立方体、圆锥体、棱锥体、圆柱体、棱柱体和长方体。
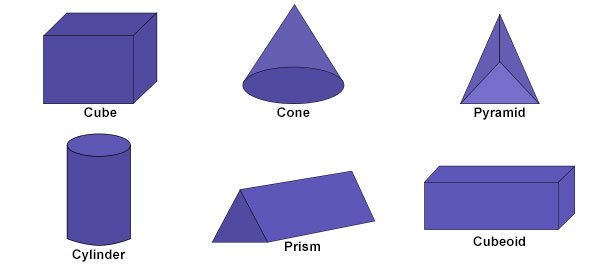
周长
封闭曲线的边界长度称为周长。我们无法找到开放曲线的周长。
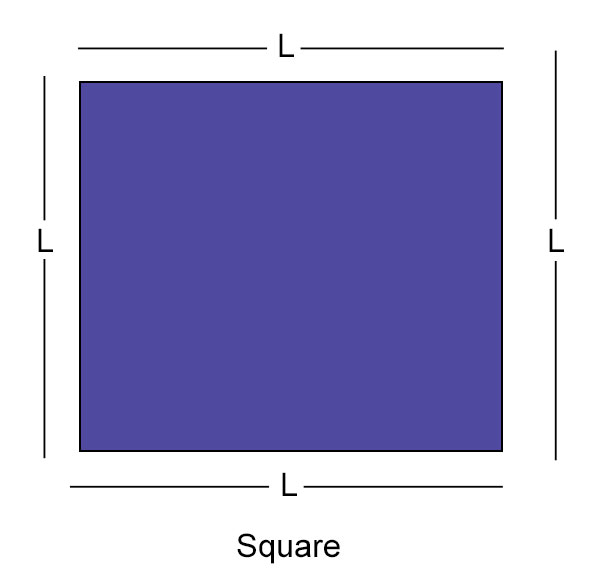
正方形的周长
正方形有四条相等边。因此,我们有以下公式:
正方形的周长 = 其各边的和
将每条边的长度表示为 L,周长表示为 P,
P = 4 × L
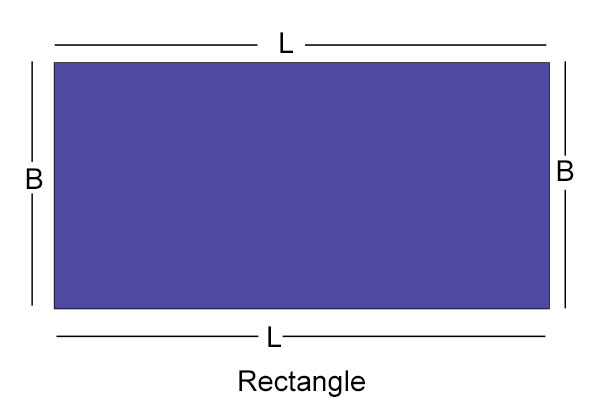
矩形的周长
矩形的对边相等。
设 L = 长度,B = 宽度,则其周长为:
P = L + L + B + B
或 P = 2L + 2B
规则多边形的周长
如果所有边和角都相等,则多边形称为规则多边形。
假设 L = 每条边的长度,
等边三角形的周长 = 3 × L = 3L
正方形的周长 = 4 × L = 4L
正五边形的周长 = 5 × L = 5L
正六边形的周长 = 6 × L = 6L
规则多边形的周长是它具有的边数乘以每条边的长度。因此,
P = n × L
其中“n”是规则多边形的边数。
矩形和正方形的面积
矩形和正方形是两种广泛使用的规则形状。我们可以使用方格纸或格点纸来找到矩形或正方形的面积。
矩形的面积
矩形的对边长度相等。矩形的较长边称为长度,较短边称为宽度。
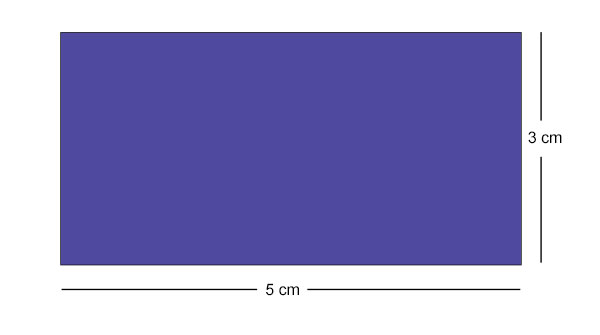
让我们使用方格纸来找到它的面积。
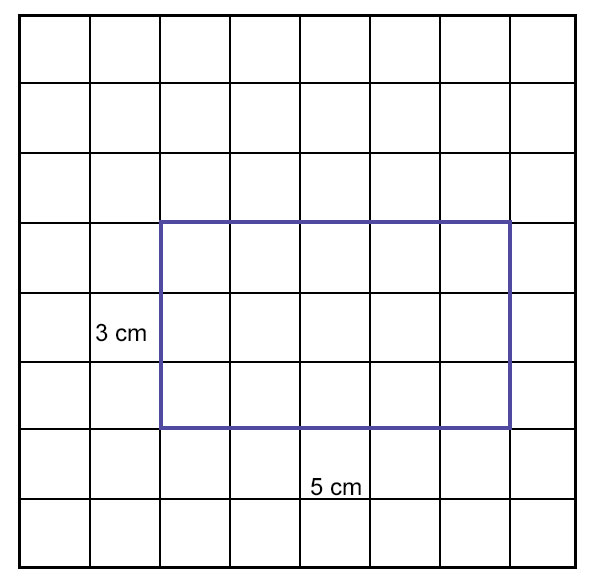
矩形包含了 15 个完整的方格。
每个方格的尺寸为 1 平方厘米。
因此,矩形的面积为 15 平方厘米。
观察到,
15 平方厘米 = (5 厘米 × 3 厘米) = (长度 × 宽度)
由此,我们可以得出结论,
矩形的面积 = (长度 × 宽度)
示例
A rectangle has a length of 8 cm and a breadth 5 cm. What is its area?
Area of the rectangle = Length × breadth
= 8 cm × 5 cm
= 40 sq. cm.
正方形的面积
正方形的四条边长度相等。
让我们取一个边长为 8 厘米的正方形,并找到它的面积。

在方格纸上绘制正方形。
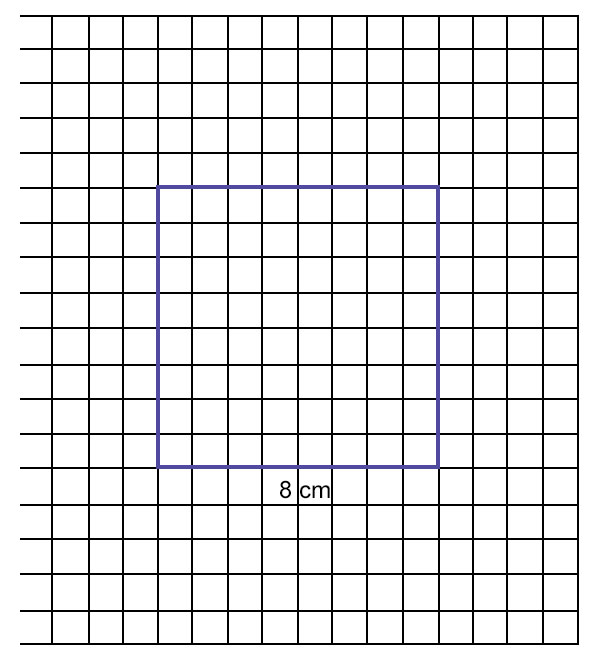
正方形包含了 64 个完整的方格。因此,它的面积为 64 平方厘米。
观察到,正方形的面积为:
64 平方厘米 = (8 厘米 × 8 厘米) = (边长 × 边长)
我们可以得出结论,
正方形的面积 = 边长 × 边长
示例
A square has a side of length 10 cm. Find its area.
Area of the square = Side × Side
= 10 cm × 10 cm
= 100 sq. cm.
不规则图形的面积
图形边界内包含的区域称为其面积。我们通常使用方格纸(或格点纸)来找到规则和不规则图形的面积。
如何使用方格纸?
有一些关于如何使用方格纸来找到封闭图形的面积的规则。
- 完全覆盖的方格 = 1 平方单位
- 覆盖 ${1}/{2}$ 的方格 = ${1}/{2}$ 平方单位
- 覆盖少于 ${1}/{2}$ 的方格 = 0 平方单位
- 覆盖多于 ${1}/{2}$ 的方格 = 1 平方单位
不规则图形的面积
让我们使用上述规则来找到不规则图形的面积。
示例:使用方格纸找到给定图形的面积。

解答:让我们绘制图形的轮廓,并计算完全覆盖、${1}/{2}$ 覆盖、多于和少于 ${1}/{2}$ 覆盖的方格的数量。
现在,让我们应用规则来计算面积
| 覆盖面积 | 数量 | 面积(平方单位) |
|---|---|---|
| 完全覆盖 | 2 | 2 × 1 = 2 |
| ${1}/{2}$ 覆盖 | 1 | 1 × ${1}/{2}$ = ${1}/{2}$ |
| 多于 ${1}/{2}$ 覆盖 | 4 | 4 × 1 = 4 |
| 少于 ${1}/{2}$ 覆盖 | 7 | 7 × 0 = 0 |
总面积 = 2 + ${1}/{2}$ + 4 = 6${1}/{2}$ 平方单位。