
第十一章 - 代数
代数导论
数学的分支
数学有几个分支,但大体上可以分为三种类型
- 算术 - 它处理数字、数字的类型、数字的属性、数字运算、数字的应用等等。
- 几何 - 它处理1维、2维和3维中不同类型的形状和图形。
- 代数 - 它是数学的一个分支,它使用变量的概念来求解方程式中未知量的值。
什么是代数?
代数很像算术,因为它使用了算术的所有主要规则和运算。但是,它引入了一个新的概念,即需要找到的未知量的概念。代数使用算术运算,如加法、减法、乘法和除法。
代数中的变量
在代数中,我们使用字母或符号来表示值未知的事物或对象。这些字母或符号被称为变量。
当有多个未知数时,会使用多个字母或符号。
探索变量
变量用于建立不同已知量和未知量之间的关系。变量用字母或符号表示。
关系式写成包含变量、数字和运算的方程式。
示例
Question: Sam and Jack are two friends. Jack is older than Sam by 3 years.
Express the relationship between their ages.
Solution:
The relationship between their ages can be expressed as,
Sam's age + 3 = Jack's age
If Sam's age is taken as X, then
Jack's age = X + 3
If Jack's age is taken as Y, then
Sam's age = Y − 3
示例:在下面的火柴盒正方形图案中,找出正方形数量和火柴棒数量之间的关系。

解答:
分析正方形的图案,
第一个正方形有4根火柴棒 = 1 + (3 × 1)
第二个正方形有7根火柴棒 = 1 + (3 × 2)
第三个正方形有10根火柴棒 = 1 + (3 × 3)
如果我们继续这个模式,那么
第N个正方形将有 1 + (3 × N) 根火柴棒。
示例
Question: Jack transfers potatoes from a sack equally into two boxes.
He finds that there are 7 potatoes still left out in the sack.
Find a relation to express the total number of potatoes.
Solution:
Let's assume the no. of potatoes in each box = P
And, total number of potatoes = T
Then,
Total no. of potatoes in the sack = potatoes in each box + leftover potatoes
T = (2 × potatoes in each box) + 7
T = (2 × P) + 7
T = 2P + 7
在几何中使用变量
让我们看看代数如何利用其强大的变量概念来处理数学规则和公式。
示例:推导出一个求正方形周长的公式。
解答:已知正方形有四个相等边,其周长为其边长的四倍。

让我们假设:
P = 正方形的周长,并且
L = 每条边的长度
那么,正方形的周长可以写成:
P = 4L
示例:推导出一个求正多边形周长的公式。
解答:多边形是一个至少有3条边的封闭图形。正多边形是指具有相等边长的多边形。正多边形的例子有等边三角形、正方形、正五边形等。
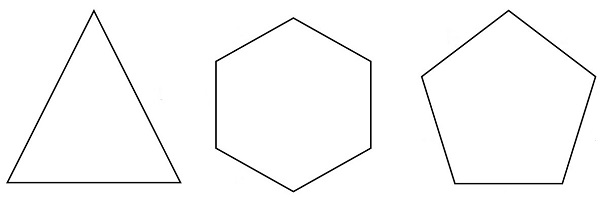
设 L = 每条边的长度
多边形的周长是其各边长度的总和。
因此,我们有以下公式:
三角形的周长 = 3L
正方形的周长 = 4L
正五边形的周长 = 5L
推广这个模式,
N边正多边形的周长 = N × 每条边的长度
= N × L = NL
矩形的周长
在矩形中,对边平行且长度相等。
考虑一个矩形PQRS,其中PQ和RS为其长度,QR和SP为其宽度。
让我们假设:
L = 矩形的长度
B = 矩形的宽度
P = 矩形的周长
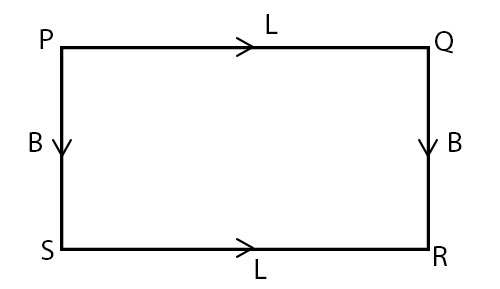
矩形的周长是其两条长度和两条宽度的总和。因此,
P = PQ + QR + RS + SP
= L + B + L + B
= 2L + 2B
= 2(L + B)
因此,任何矩形的周长的通用公式是:P = 2(L + B)
矩形的面积
让我们假设:
A = 矩形的面积
矩形的面积是其长度和宽度的乘积。因此,
面积 = 长度 × 宽度
A = L × B = LB
半径和直径
圆的直径是其半径长度的两倍。
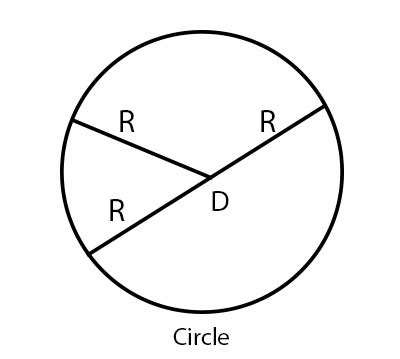
假设:
D = 圆的直径
R = 圆的半径
那么,
D = 2 × R = 2R
将变量与算术运算结合使用
交换律
此属性指出,更改运算中数字的顺序不会影响结果。例如,
5 + 4 = 9 和 4 + 5 = 9
让我们把它写成代数公式的形式。
如果A和B是两个变量,那么
A + B = B + A
交换律适用于加法和乘法。
减法和除法不满足交换律。
A − B ≠ B − A
A ÷ B ≠ B ÷ A
结合律
三个或更多数字的和或积保持不变,无论数字如何分组。例如,
2 × 5 × 4 = (2 × 5) × 4 = 10 × 4 = 40
2 × 5 × 4 = 2 × (5 × 4) = 2 × 20 = 40
结合律适用于加法和乘法,但不适用于减法和除法。
让我们使用A、B和C作为变量来概括公式:
(A + B) + C = A + (B + C)
(A × B) × C = A × (B × C)
分配律
分配律帮助我们解决复杂的乘法问题。例如,
7 × 45
= 7 × (40 + 5)
= (7 × 40) + (7 × 5)
= 280 + 35 = 315
在这里,我们将乘法分配给每个被加数。
使用变量概括分配律:
A (B + C) = (A × B) + (A × C)
其中A、B和C是代表任何三个不同数字的变量。
带有变量的代数表达式
数学表达式定义为两个或多个数字,它们相互加、减、乘或除。
例如,2 + 3 是一个数学表达式。
表达式分为两种类型
- 数值表达式
- 代数表达式
数值表达式
只包含数字的数学表达式称为数值表达式。例如,(5 + 9) 或 (7 − 3) 是数值表达式。
代数表达式
包含代数变量的数学表达式称为代数表达式。例如,(x + 2) 或 (y − 3) 称为代数表达式,因为它们包含 x 和 y 等变量。
BODMAS规则
我们使用BODMAS规则来简化数值和代数表达式。此规则列出了不同运算(如加法、减法、乘法和除法)的执行优先级。
括号 >> 阶 >> 除法 >> 乘法 >> 加法 >> 减法
示例
Question: Simplify 18 + (6 × 3) + (5 − 6)
Solution:
First priority is brackets. Simplifying the numbers inside the brackets first,
18 + (6 × 3) + (5 − 6)
= 18 + 18 − (−1)
= 18 + 18 − 1
Next priority is addition,
18 + 18 − 1 = 36 − 1
Last priority is subtraction,
36 − 1 = 35
So, we have,
18 + (6 × 3) + (5 − 6) = 35
示例
Question: Simplify (y × 7) + (2(3 − y))
Solution:
Using BODMAS rule,
(y × 7) + (2(3 − y))
= 7y + (6 − 2y)
= 7y + 6 − 2y
= 5y + 6
So, (y × 7) + (2(3 − y)) = 5y + 6
示例
Question: Jack has 5 more chocolates than Jill and Sam has twice as many chocolates as Jack. Develop an algebraic expression for the number of chocolates with Sam. Solution: Assume that Jill has y chocolates. Number of chocolates with Jack = y + 5 Number of chocolates with Sam = 2 (y + 5) = 2y + 10
示例:一辆汽车行驶在相距D公里的两个城市之间。汽车行驶了5小时,距离目的地150公里。推导出汽车速度的代数表达式。
解答:
两城市之间的距离 = D公里
汽车行驶的距离 = D − 150公里
汽车的行驶时间 = 5小时
因此,我们有:
汽车速度 = ${行驶距离}/{行驶时间}$ = ${D - 150}/{5}$ 公里/小时
猜数字游戏
代数魔术
让你的朋友想一个数字。它可以是她选择的任何自然数。
然后,让她对其执行以下一系列算术运算。

你的朋友可以想任何数字,但上述运算结束后的最终输出将是10!
惊讶!让我们找出它是如何工作的。
假设你的朋友想到的数字是 = N
加2,它变成:
N + 2
乘以2:
2(N + 2) = 2N + 4
加5:
2N + 4 + 5 = 2N + 9
乘以5:
5 (2N + 9) = 10N + 45
减去45:
10N + 45 − 45 = 10N
除以N:
$${10 \: N}/{N} = 10$$
因此,N可以是任何数字,但我们的输出保持不变。
另一个例子
让另一个朋友想一个自然数,并一步一步地执行以下算术运算。

无论你的朋友想到什么数字,这个运算序列的最终输出都将是6!
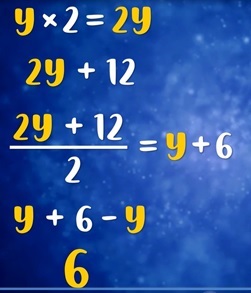
什么是方程?
方程是一个带有“等于”号(=)的语句,表示两边表达式的值相等。
数值方程
如果方程两边的表达式只有数字,那么这样的方程就是一个数值表达式。例如,
5 − 3 = 2
10 + 7 × 2 = 24
代数方程
如果方程两边的表达式包含一个或多个变量,那么这样的方程就是一个代数方程。例如,
x + y = 12
6n = 72
我们求解代数方程以找到方程中未知变量的值。例如,
4 + x = 6
从方程两边减去4可以隔离未知变量并给出其值。
4 + x − 4 = 6 − 4
⇒ x = 2
同样,求解
4y = 60
⇒ ${4y}/{4}$ = ${60}/{4}$
⇒ y = 15
示例:字母“W”可以用4根火柴棒组成。我们有方程 M = 4N,其中 M 是火柴棒的总数,N 是形成的“W”的数量。如果 M = 20,求形成的“W”的数量。
解答:
给定的方程是:
M = 4N
M = 20,所以方程变为:
20 = 4N
求解N:
N = ${20}/{4}$ = 5
因此,可以用20根火柴棒组成5个“W”。
示例
Question: Jack has 3 more chocolates than Jill and Jill has 5 chocolates in all. How many chocolates does Jack have?
Solution:
Let the number of chocolates with Jack = Y.
Jill has 3 chocolates less than Jack, which is = Y − 3
Given that Jill has 5 chocolates in all.
So, we have the equation,
Y − 3 = 5
Adding 3 on both sides,
x − 3 + 3 = 5 + 3
⇒ x = 8
Therefore, Jack has 8 chocolates.