
第五章 - 认识基本图形
引言
线段、角、三角形、四边形、多边形和圆是基本图形的例子。任何复杂的几何图形都可以由这些基本图形构成。
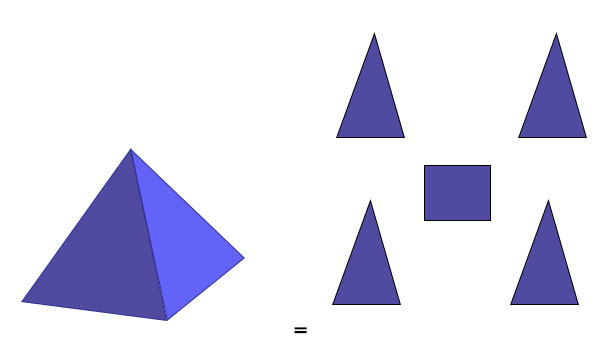
例如,一个正四棱锥是由四个等腰三角形和一个正方形底面组成的。
一个六棱柱是由6个矩形和两个六边形组成的。
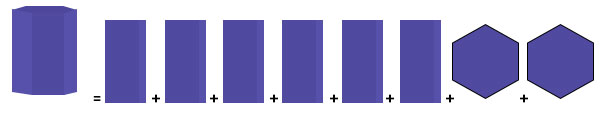
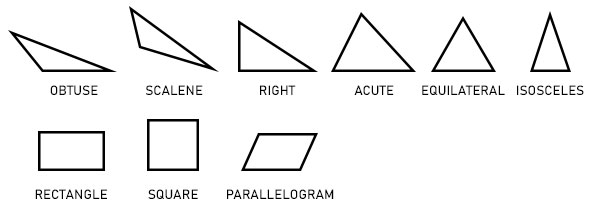
即使是基本图形也有不同的形式,例如三角形可以是等边三角形、等腰三角形或不等边三角形。类似地,四边形可以是矩形、正方形或平行四边形。
测量线段
线段的长度用毫米和厘米来测量。
观察比较
如果我们将两条线段并排放置,那么只需观察就可以很容易地比较它们的长度。

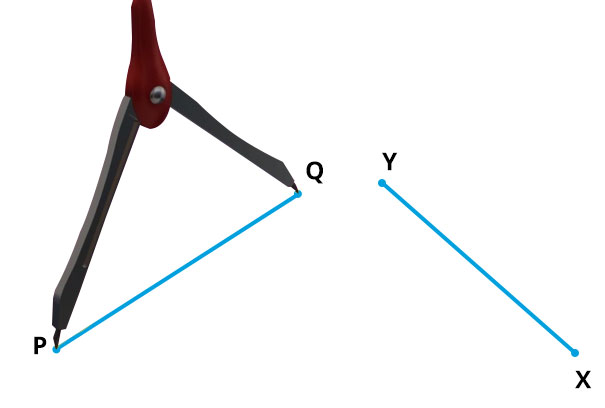
使用量角器比较
当两条线段长度几乎相等时,我们必须使用量角器来比较它们的长度。(原文此处应为“卡尺”或“圆规”,此处根据上下文进行调整)
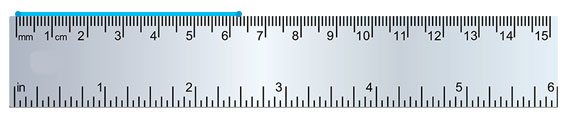
使用尺子测量
尺子标有厘米和毫米。尺子上两个大刻度之间的差是1厘米,而两个小刻度之间的差是1毫米。
将尺子沿着线段放置,尺子的零点与线段的一个端点对齐,测量另一个端点在尺子上的读数,即可得到线段的长度。
使用尺子和量角器测量
首先,使用量角器,将其两臂张开,固定在线段的两端点上。(原文此处应为“卡尺”或“圆规”,此处根据上下文进行调整)
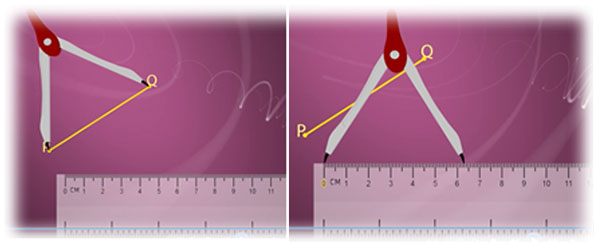
然后,拿起量角器,将其放在尺子上,使量角器的一臂与尺子的零点重合。(原文此处应为“卡尺”或“圆规”,此处根据上下文进行调整)从量角器的另一臂上读取读数。(原文此处应为“卡尺”或“圆规”,此处根据上下文进行调整)
角的类型
平行线
平行线永不相交。

相交线
当两条线在一点相交时,它们被称为相交线;交点被称为交点。
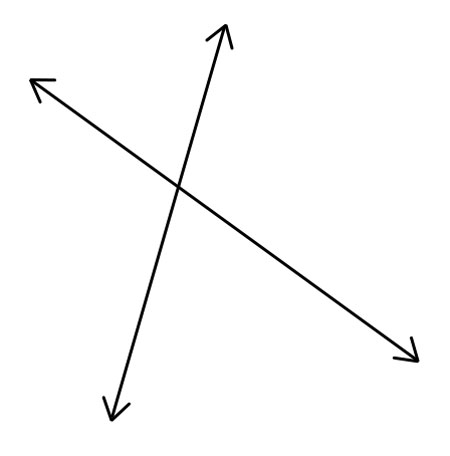
两条相交线形成四个角;通常是两个锐角和两个钝角。
垂直线
构成“+”号的两条线称为垂直线。垂直线形成的角称为直角。
角
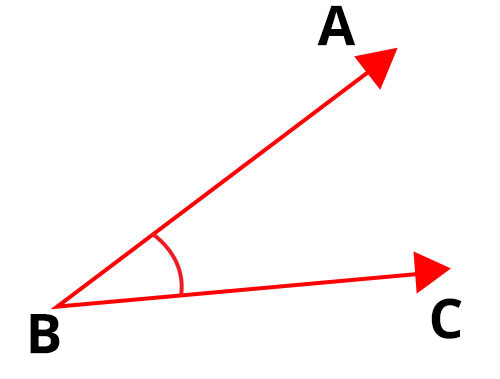
当两条线段在一点相交时,它们形成一个角。线段称为角的边。ABC是一个角。
直角
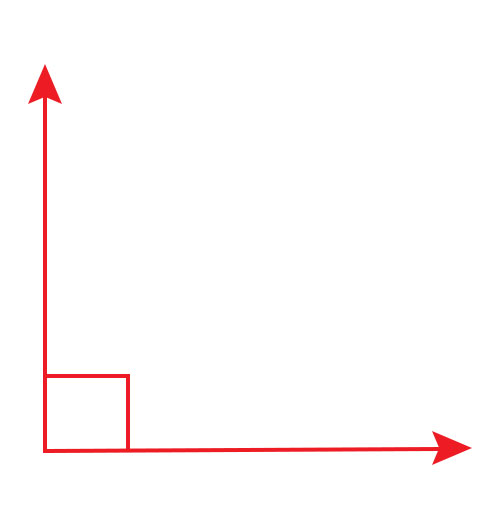
呈“L”形的角称为直角,角的两边互相垂直,或成90°。
锐角
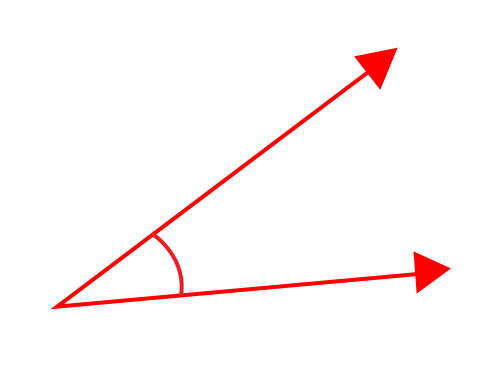
小于直角(90度)的角称为锐角。
钝角
大于直角(90度)但小于平角的角称为钝角。
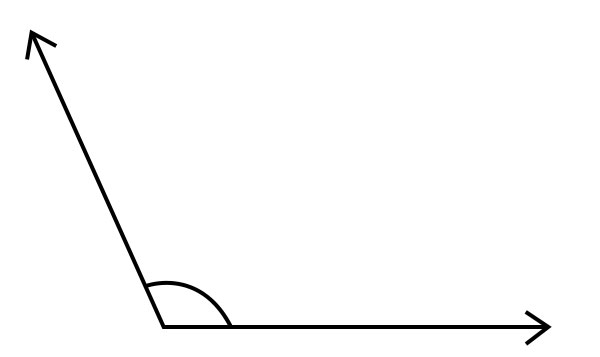
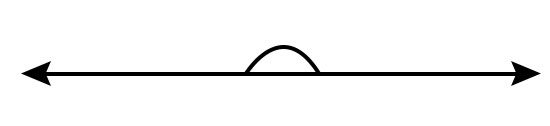
平角
当形成角的射线指向完全相反的方向时,就会形成平角。平角等于180°。
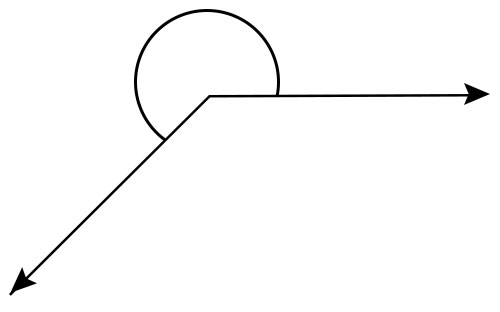
优角
介于180°和360°之间的角称为优角。
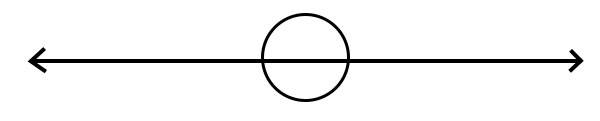
周角
当角的一条边绕着另一条边(底边)旋转一周时,就会形成周角。周角等于360°。
测量角
角是用一种叫做量角器的工具来测量的,这种工具可以在文具盒里找到。
就像尺子一样,量角器也有刻度,但形状是半圆形。角的单位是度。刻度从0°开始,到180°结束。
测量锐角
将量角器放置在角的顶点处,使其中心与顶点重合。
确保量角器的0°线或基线与锐角的底边重合。
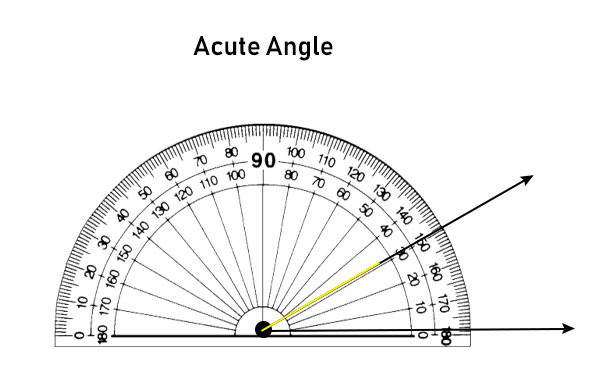
从角的另一条边在量角器上的位置记录测量值。
测量直角
当角的另一条边指向量角器上的90°时,它被称为直角。

测量钝角
当角的另一条边指向量角器上90°到180°之间的任何位置时,它就是一个钝角。

测量优角
优角的度数介于180°和360°之间。我们不能直接用量角器测量优角,因为它最大只能测量180°。因此,优角是间接测量的。
锐角/钝角的一对边在相对侧也形成一个优角。在这种情况下,锐角/钝角的度数 = 360° - 优角的度数。

测量平角和周角
平角的度数为180°。使用量角器,可以测量平角,显示180°的读数。周角的度数为360°,是平角度数的两倍。
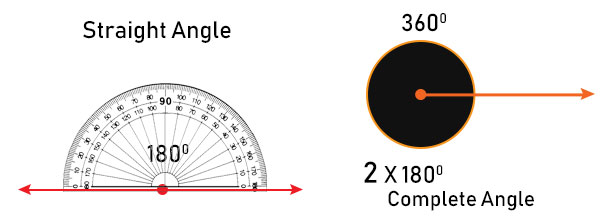
垂直平分线
平分线是一条将另一条线段分成两等份的线。如果一条线与另一条线成90°角,则称这条线垂直于另一条线。然后称这两条线为垂直线。
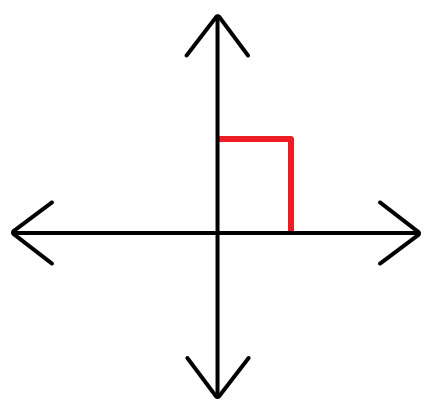
线段的垂直平分线必须垂直于它,并且也将其分成两等份。
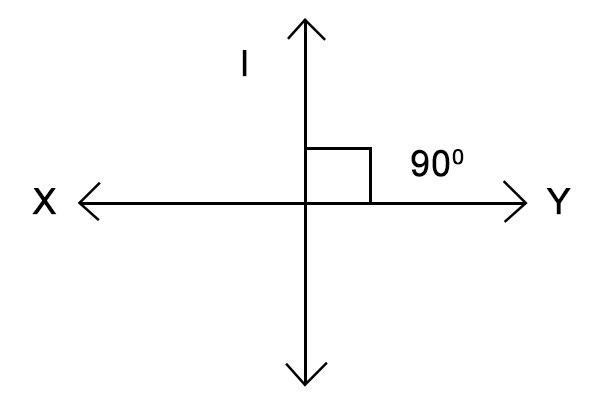
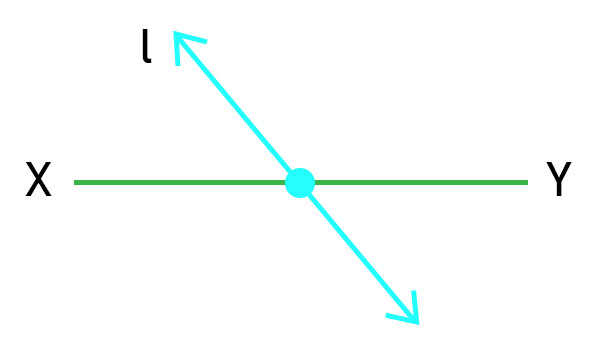
在下面的例子中,平分线不垂直于XY,所以它不是垂直平分线。
三角形的类型
三角形是一种基本图形,它是边数最少的几何图形。三角形有三条边和三个角。
我们可以根据三角形的边和角的特性对其进行分类。
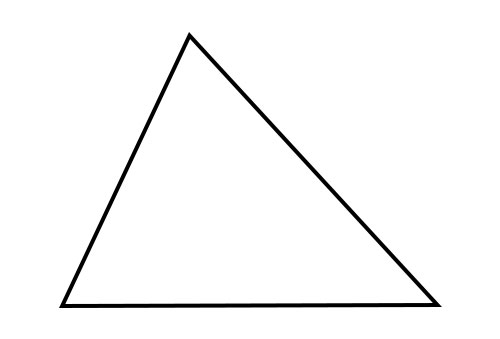
锐角三角形
如果三角形的所有角都小于90°,则该三角形是锐角三角形或锐角三角形。
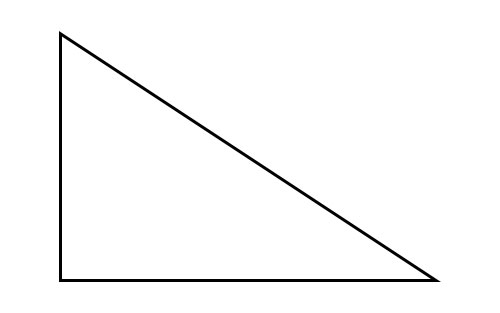
直角三角形
如果三角形的两个角是锐角,第三个角是直角或90°,则这样的三角形称为直角三角形。
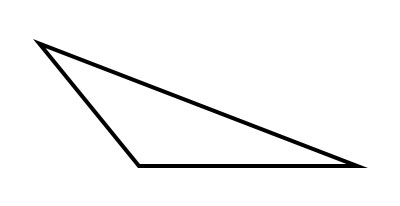
钝角三角形
如果三角形的两个角是锐角,第三个角是钝角或大于90°的角,则这样的三角形称为钝角三角形或钝角三角形。
等边三角形
在一个三角形中,如果三条边的长度相等,则该三角形称为等边三角形。在等边三角形中,所有角都等于60°。
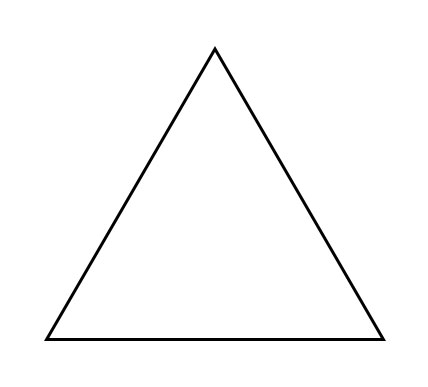
等腰三角形
在一个三角形中,如果发现两条边的长度相等,则该三角形称为等腰三角形。在等腰三角形中,与相等边相对的角也相等。
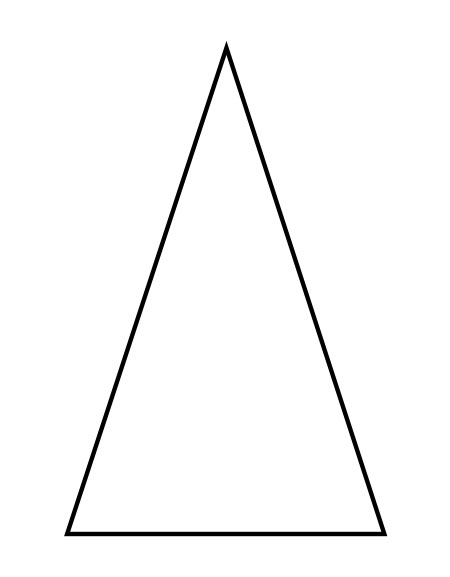
不等边三角形
在一个三角形中,如果边的长度不同或不相等,则该三角形称为不等边三角形。它的三个角也不相等。
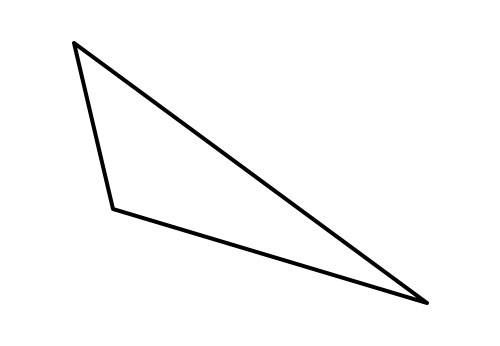
四边形的类型
四边形是一种有四条边和四个角的多边形。四边形有很多类型,例如矩形、正方形、平行四边形、菱形和梯形。
矩形
矩形是一种四边形。它有两对边长度相等且互相平行。所有角都等于90°。
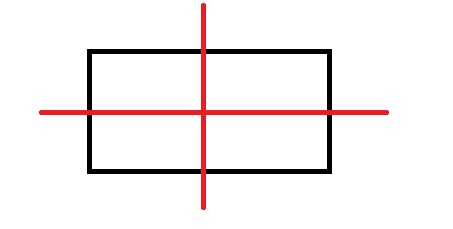
矩形的对角线长度相等,并且互相平分。
正方形
正方形的所有边都相等且互相平行。所有角都等于90°。

正方形是矩形的一种特殊情况,其中长和宽相等。对角线互相垂直平分。
平行四边形
这是一种四边形,其中对边相等且互相平行。对角相等,邻角不相等。
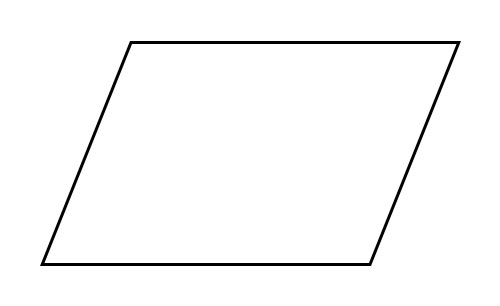
所有矩形和正方形都是平行四边形。但并非所有平行四边形都是矩形或正方形。
菱形
菱形是一种特殊的四边形,它的所有边都相等。
- 对边相等且互相平行。
- 对角相等,但邻角不相等。
- 对角线不相等,但互相垂直平分。

- 所有菱形都是平行四边形,但并非所有平行四边形都是菱形。
- 所有正方形都是菱形,但并非所有菱形都是正方形。
梯形
梯形是一种四边形,其中有一对对边平行。
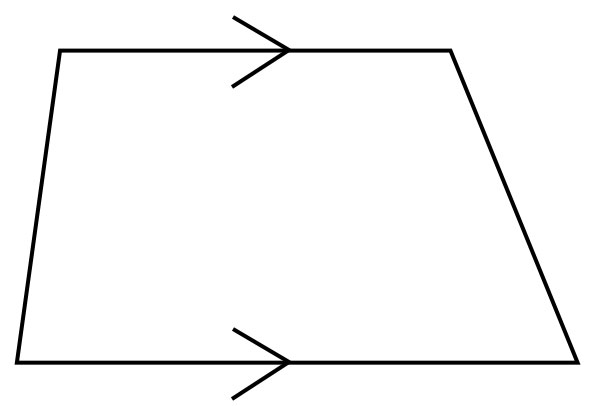
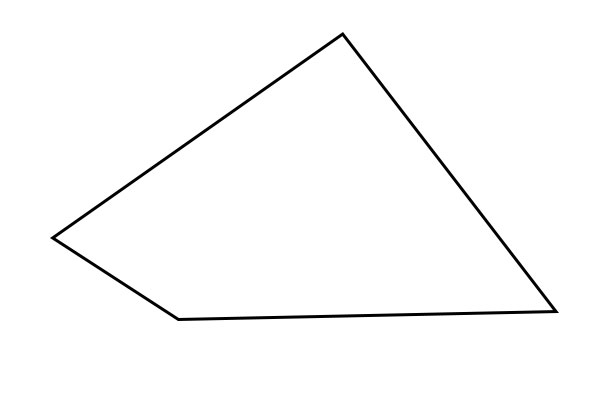
四边形
任何四边形都称为四边形。矩形、正方形、梯形、平行四边形和菱形都是四边形的特殊类型。没有边或角相等的四边形是普通四边形。
四边形的对角线
- 矩形和正方形的对角线相等。
- 平行四边形和菱形的对角线不相等。
- 正方形和菱形的对角线互相垂直。
- 矩形、正方形、平行四边形和菱形的对角线互相平分。
多边形的类型
多边形是由线段组成的封闭图形。多边形的名称取决于它们有多少条边。
- 三角形是边数最少的多边形,即三条边。
- 四边形是有四条边的多边形。
- 五边形是一个五边多边形。
- 六边形是一个六边多边形。
- 八边形是一个八边多边形。
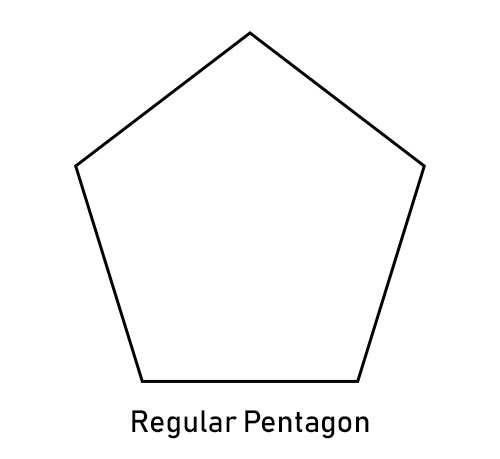
正多边形
边长相等且角相等的多边形称为正多边形。
不正多边形
边长和角不相等的多边形称为不正多边形。
随着多边形边数的增加,其形状越来越接近圆形。因此,圆可以看作是一个具有无限多条边的多边形。
多边形的对角线
对角线是连接多边形中任意两条不相邻顶点的线段。
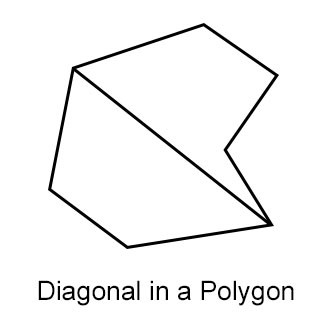
N边形对角线的数量由公式 ${N (N − 3)}/{2}$ 给出。
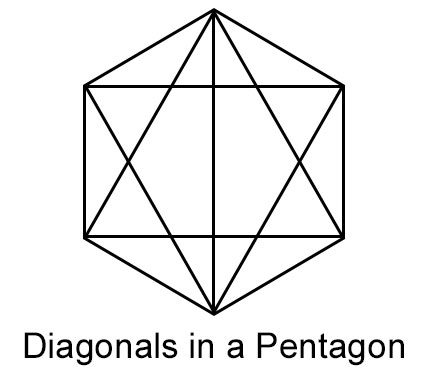
五边形的对角线条数 = ${5(5 − 3)}/{2}$ = 5
六边形的对角线条数 = ${6(6 − 3)}/{2}$ = 9

三维形状
维度
- 点是一个具有固定位置的微小点。它没有维度。
- 线是一维点集,具有长度。
- 平面是线的集合。它具有两个维度:**长度**和**宽度**。
- 长方体是线的集合,具有三个维度:**长度**、**宽度**和**高度**。
一些基本的二维基本形状
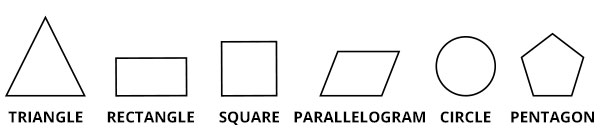
我们可以用这些二维基本形状构建三维形状。
长方体
三维长方体是由许多矩形组合而成的。
- 它有6个面或平面。
- 这些面在称为**棱**的线上相交。长方体有12条棱。
- 三条或更多条棱在称为**顶点**的点上相交。长方体有8个顶点。

正方体
正方体是由许多正方形组合而成的。它也像长方体一样有6个面、12条棱和8个顶点。
- 在正方体中,所有棱都相等。在长方体中,棱的长度不相等。
- 所有正方体都是长方体,但并非所有长方体都是正方体。

三角棱柱
三角棱柱是一个三维形状,它有5个面,即两个三角形底面和3个矩形侧面。它有9条棱和6个顶点。

棱柱可以由矩形底面、正方形底面、五边形底面和六边形底面构成。
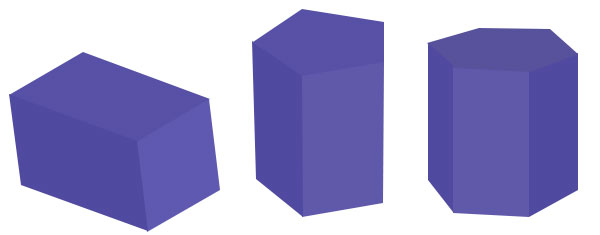
矩形棱柱只有长方体,正方形棱柱只有正方体。
正方形锥体
它是由正方形和三角形构成的三维形状。它有一个正方形底面和4个三角形侧面。它有5个面、8条棱和5个顶点。
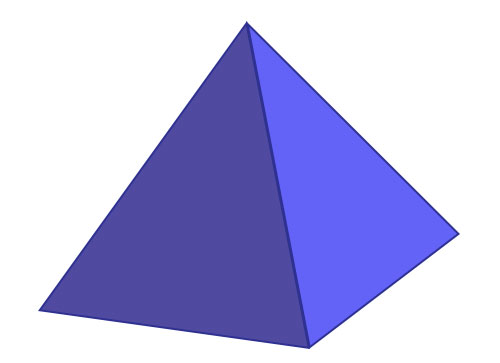
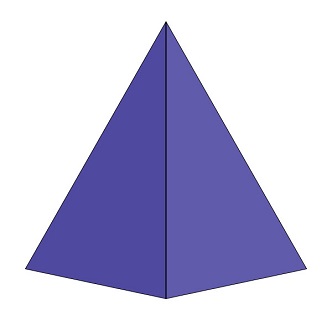
三角锥体或四面体
它是由四个三角形构成的三维形状。它有4个三角形面、6条棱和4个顶点。
圆柱体、圆锥体和球体
圆柱体、圆锥体和球体是没有直边的三维形状。
- 圆柱体由两个圆和一个矩形构成。它有两个圆形底面。
- 圆锥体由一个圆形底面和一个扇形构成。
- 球体没有底面、面、棱和顶点。球体是二维圆的三维版本。
