
第4章 - 基本几何概念
几何图形简介
术语“几何”来自希腊语Geometron。Geo表示地球,metron表示测量。几何概念体现在各种艺术形式、测量、建筑、工程和设计中。
从桌子和书本等基本物体到世界著名的纪念碑,一切都可以用它们的几何形状来定义。
著名纪念碑及其形状
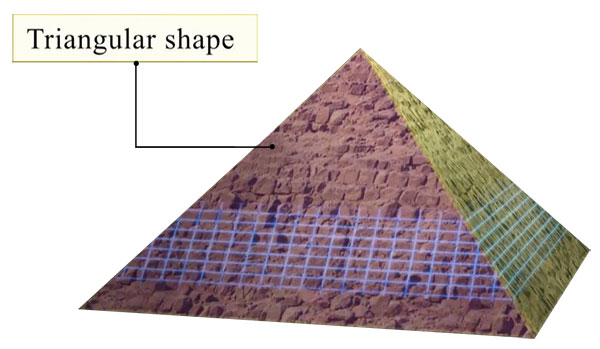
吉萨大金字塔以其独特的形状而闻名。金字塔的所有面都是三角形,底座是正方形。
泰姬陵有正方形底座、圆形穹顶和四个圆柱形尖塔。

比萨斜塔有圆形底座和圆柱形塔身。

不仅是著名的纪念碑,我们还可以用几何形状来定义即使是最简单的物体,例如书籍、桌子和瓶子。
点、线段、射线和直线
像正方形和三角形这样的几何图形由点、线、射线和角等基本单元组成。
点
拿一支削尖的铅笔,在一张纸上画一个点。这个点是无形的细小点。这个微小的点叫做点。
我们在几何图形上使用点来标记特定位置。当我们将几个点放在一起时,我们用A、B、C、D等命名它们,以便于识别。
线段
我们将两个点连接起来得到一条线段。线段${AB}↖{−}$连接点A和B。

直线
如果线段在A方向以外延伸,在B方向以外延伸,没有终点,那么我们就得到一条直线。直线表示为${AB}↖{↔}$。

相交线和平行线
当两条直线在某一点相遇时,我们称它们为相交线,它们的交点称为交点。
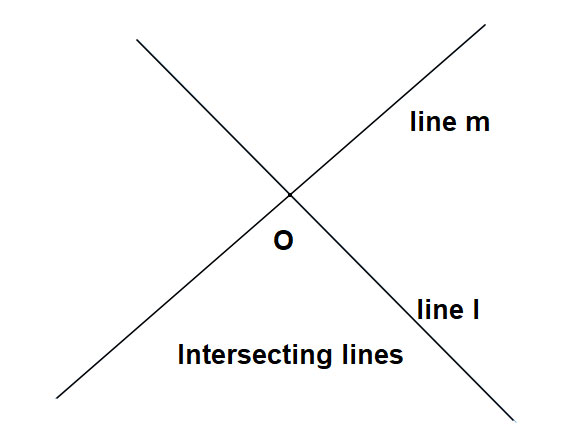
当两条直线永不相交时,我们称它们为平行线。
射线
射线是直线的一部分,它从直线上的一个点开始,并无限地朝某个方向延伸。
射线${AB}↖{→}$从A开始,向B方向延伸,并超出B。
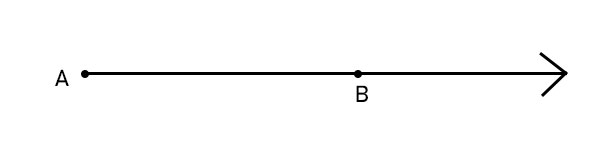
在几何上,射线有一个起点,没有终点。当手电筒或灯泡发光时,我们会得到光线。我们也从太阳那里得到光线。
曲线和多边形
曲线可以定义为点在任何方向上的连续运动。因此,所有可能的形状都可以归类为曲线,因为所有形状都是由点在单维或多维空间中的运动形成的。
项链、蛇和松弛的绳索是曲线图形的一些例子。

通常,曲线是不直的实体,但在数学中,即使是直线也是曲线。
曲线的类型
- 有些曲线不会与自身相交。这些称为简单曲线。
- 没有开口的曲线称为闭合曲线。
- 不闭合路径的曲线称为开曲线。
多边形
在数学上,多边形是二维闭合图形,完全由线段组成。构成多边形的线段称为多边形的边。
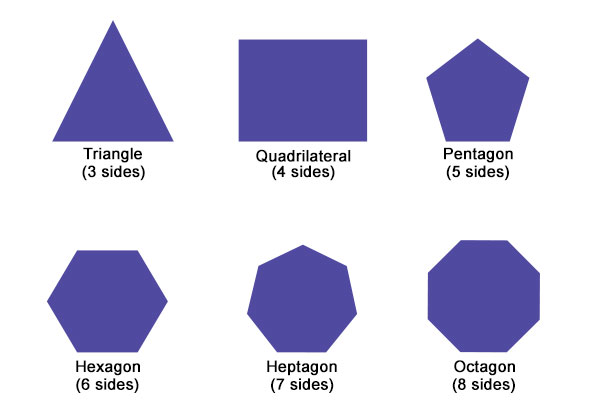
两条边相交的公共点称为顶点(单数形式为顶点)。多边形的顶点数等于其边数。