第14章 - 实践几何

实践几何简介

从像桌子和书这样的基本物体到世界著名的纪念碑，一切都可以用它们的几何形状来定义。

几何盒

我们可以借助几何盒中提供的工具绘制基本几何图形，如线段、三角形、矩形和圆形。

尺子 - 使用此工具绘制均匀的线段。
圆规 - 使用此工具比较两条线段的长度。
圆规 - 绘制弧线或圆形
三角板 - 绘制三角形或垂直线
量角器 - 测量角度
其他（铅笔、橡皮擦、卷笔刀） - 使用这些工具进行绘图。

几何思想体现在所有形式的艺术、测量、建筑、工程和设计中。

线段和圆的作图

可以使用尺子绘制线段，可以使用圆规绘制圆形。

绘制线段

要使用尺子绘制线段，

考虑我们选择的长度，例如 10 厘米。
取尺子，从 0 厘米到 10 厘米绘制一条线段。

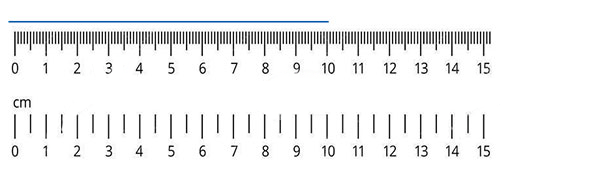
我们还可以使用尺子来测量和比较不同线段的长度。

比较两条线段

我们使用圆规来比较不同线段的长度。

将圆规两脚的尖端固定在线段的两端。
两脚之间的间隙越大，线段越长。

也可以使用圆规和尺子来测量线段的长度。

使用圆规绘制圆形

让我们将圆的半径固定为 4 厘米。

取一把尺子，将圆规的两臂伸展，使一只臂固定在 0 处，另一只臂固定在 4 厘米处。
用手握住圆规顶部，并将圆规的另一臂牢牢地固定在纸上，然后旋转铅笔臂。

这样，我们就绘制了一个半径为 4 厘米的完美圆形。

垂直线的作图

与另一条线成 90° 角的线称为该线的垂线。可以使用三角板或圆规绘制垂直线。

有四种方法可以绘制垂直线。

方法 1 - 使用尺子和三角板

画一条线 c 并在其上标记一个点 A。
将尺子的一条边沿 l 放置。
将三角板放在线上，使其 90° 朝向的边与线重合。
沿着尺子的边缘滑动三角板，直到其直角角与 A 重合。
在三角板与 A 重合的地方画一条想要的线，并将其端点命名为 B。
新线 AB 垂直于线 c。

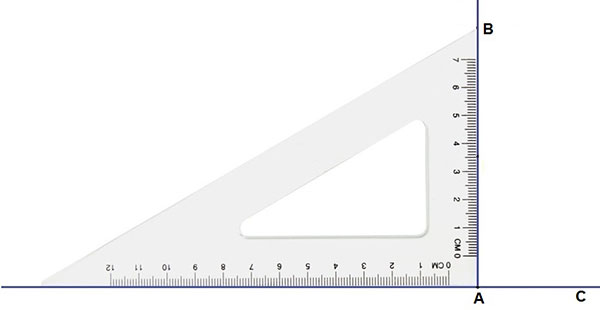
方法 2 - 使用尺子和三角板

画一条直线 l 并在其外部标记一个点 P。
将三角板放在 l 上，使其直角的一条边与 l 对齐。
将尺子放在三角板直角对面的边上。
固定尺子，然后沿尺子滑动三角板直到点 P。
当直角接触到点 P 时停止滑动。
画一条连接点 P 到线 l 的线段。

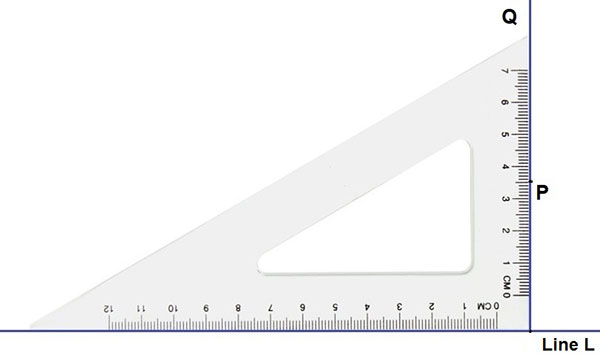
方法 3 - 使用尺子和圆规

画一条线 l 并在其上标记一个点 P。
取圆规并选择一个合适的半径。
以 P 为圆心，使用圆规绘制一条弧线。
该弧线应与线 l 相交于两点 A 和 B。
以 A 和 B 为圆心，以大于 AP 的半径绘制两条弧线，它们相交于 Q。
连接 PQ 以获得所需的垂线。

方法 4 - 使用尺子和圆规

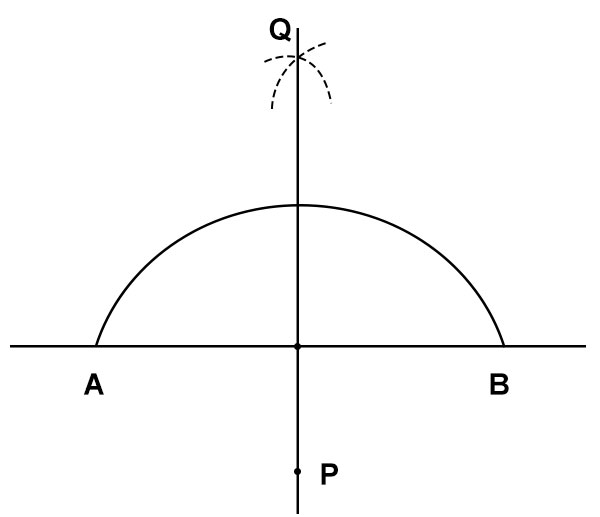
画一条线 l 并在其外部标记一个点 P。
以 P 为圆心，画一条弧线，该弧线与线 l 相交于两点 A 和 B。
使用相同的半径，以 A 和 B 为圆心，再绘制两条弧线，它们在另一侧相交于一点，例如 Q。
连接 PQ 以获得所需的垂线。

垂直平分线的作图

“平分”一词表示分成两等份。

如果我们使用一条垂直线将一条线分成两等份，那么这条垂直线称为垂直平分线。

绘制垂直平分线

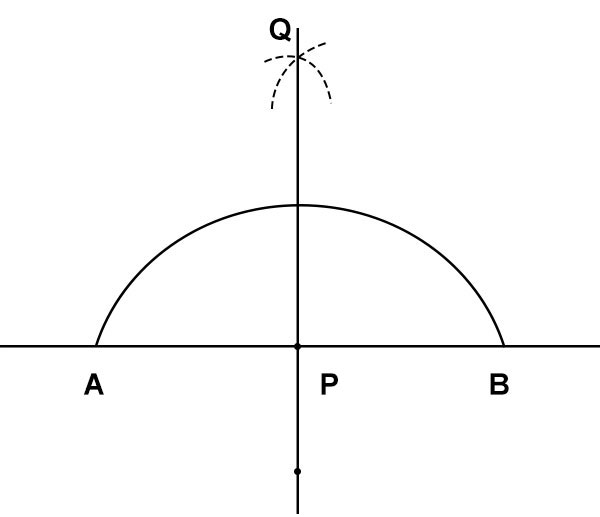
画一条任意长度的线段 AB。
以 A 和 B 为圆心，用圆规在 AB 两侧绘制四条弧线，使它们相交于两点。
将这两个点命名为 P 和 Q。
半径应大于 AB 长度的一半。
连接点 P 和 Q。它在 O 处与 AB 相交。
PQ 是 AB 的垂直平分线。

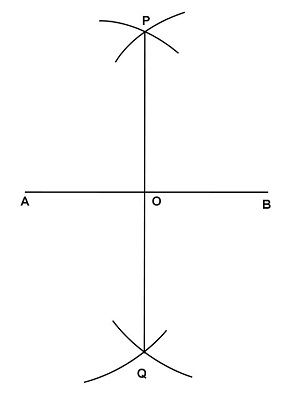
在上图中，

AO = OB = ${1}/{2}$AB

您可以使用尺子验证 AO = OB。

角的作图

由两条从一个共同点（顶点）发散的线或射线形成的图形称为角。

角可以具有不同的度数，例如 40°、60°、90°、180° 等。

使用量角器绘制角

假设我们要绘制一个 40° 的锐角。

我们使用量角器绘制角。

步骤如下

画一条任意长度的线段 AB。
取量角器，将其中心放在点 A 上。
量角器的 0° 刻度应与线段 AB 重合。
现在，使用量角器标记 40°。将此点命名为 C。
由于线段落在中心的右侧，因此标记右侧的 40°。
连接点 A 和 C。
∠BAC 是所需的角。

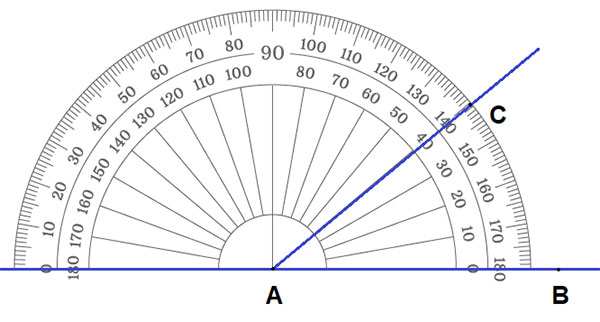
如果线段位于中心的左侧，则我们将标记量角器左侧的 40°。

角平分线的作图

角平分线是将一个角分成两个相等部分的线。例如，60° 角的平分线将产生两个各为 30° 的角。

绘制角平分线

步骤如下

假设我们有一个角 ∠A。
取圆规，选择您选择的合适半径，并以 A 为圆心绘制一条弧线
该弧线应与 ∠A 的两条边相交。
将交点标记为 P 和 Q。

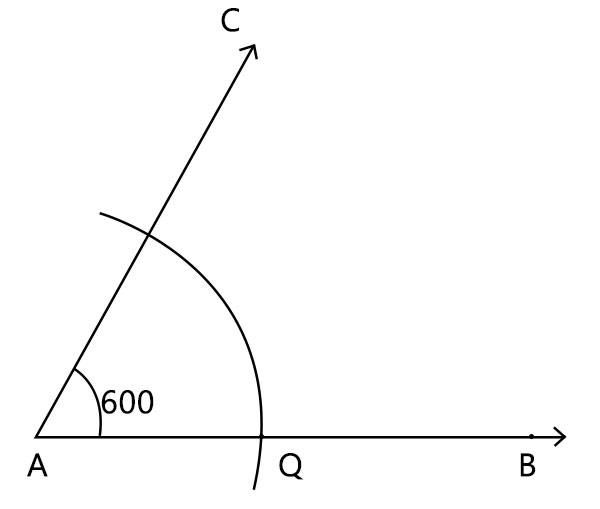
使用相同的半径，以 P 和 Q 为圆心，绘制两条弧线，使它们在一点（∠A 的内部）处相交。

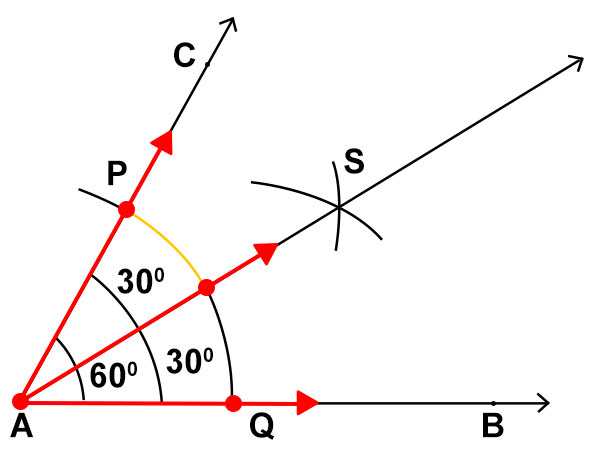
将交点命名为 S。
连接点 A 和 S。
线段 AS 是 ∠A 的角平分线。

AS 将角 ∠A 平分成两个相等的部分。

打印页面