
第2章 - 整数
整数简介
我们用于计数的数字是1、2、3、4……等等。这些数字被称为计数数或自然数。
请注意,0不是自然数序列的一部分。自然数从1开始。
一个数的前一个数
考虑数字1、2、3、4和5。
紧接在某个数之前的数称为该数的前一个数。
紧接在4之前的数是3。
所以,3是4的前一个数。
我们从一个数中减去1得到它的前一个数。
一个数的后一个数
紧接在某个数之后的数称为该数的后一个数。
紧接在4之后的数是5。
所以,5是4的后一个数。
类似地,3的前一个数是2,3的后一个数是4。
我们给一个数加上1得到它的后一个数。
整数
包含0的自然数序列称为整数。
所以数字0、1、2、3、4……是整数。这里0是1的前一个数,2是1的后一个数。

自然数是整数的一部分。
数轴上的运算
数轴
数轴中间是0。在0的右侧一小段距离处绘制1。类似地,2、3、4等等都在1的右侧绘制。
任何两个连续整数之间的固定距离称为单位距离。

加法是向右移动,减法是向左移动。
数轴上的加法
加法是在数轴上向右移动。
数轴上任何特定数字右侧的数字总是大于该数字左侧的数字。
例如,由于3位于2的右侧,所以3大于2。
示例:在数轴上计算2 + 3。
从数轴上的2开始,向右跳3步。
这给了我们,
2 + 3 = 5

示例:在数轴上计算5 + 3。
从5开始,向5的右侧跳3步。你将落在8上。
5 + 3 = 8

数轴上的减法
减法是在数轴上向左移动。
示例:在数轴上从8中减去2。
从8开始。向左移动2步,落在6上。所以,在数轴上向左移动是减法。所以,8 − 2 = 6。

示例:化简8 − 2 − 3。
从8开始。向左跳2步,落在6上。再向左跳3步,落在3上。所以8 − 2 − 3 = 3

数轴上的乘法
乘法是在数轴上从零开始,进行相同大小的跳跃多次。
示例:求3 × 2的积。
要找到3 × 2的积,我们需要从0开始,进行两次3步的跳跃。
在数轴上,乘法总是从0开始。
从0开始,向右跳3步,落在3上。
然后,再向右跳3步,到达6。
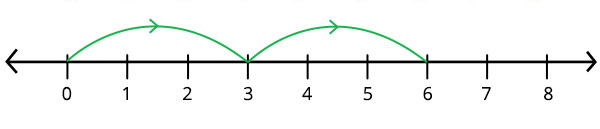
所以,3 × 2的积 = 6。
整数的性质
整数的封闭性
如果将任意两个整数相加,则得到的和是一个整数。此性质称为整数在加法下的封闭性。
整数的加法和乘法满足封闭性,而减法和除法不满足。
示例
0 + 10 = 10
3 + 8 = 11
9 + 3 = 12
如果将任意两个整数相乘,则得到的结果是一个整数。此性质称为整数在乘法下的封闭性。
示例
0 × 10 = 0
3 × 8 = 24
3 × 9 = 27
如果将任意两个整数相减,则结果可能是或可能不是整数。整数在减法下不封闭。
示例
0 − 10 = 不是整数
3 − 8 = 不是整数
9 − 3 = 6
在前两个例子中,结果不是整数。只有在第三种情况下,减法的结果才是整数。
类似地,如果一个整数除以另一个整数,则结果可能是或可能不是整数。所以,整数在除法下不封闭。
示例
${0}/{10}$ = 0
${3}/{8}$ = ${3}/{8}$,不是整数
${9}/{3}$ = 3
在第一种和第三种情况下,任意两个整数的除法结果都是整数。但在第二种情况下,结果是分数,而不是整数。
整数的交换律
如果将任意两个整数按任意顺序相加或相乘,则结果保持不变。例如,
3 + 8 = 11
8 + 3 = 11
类似地,
3 × 8 = 24
8 × 3 = 24
整数的加法和乘法满足交换律,但整数的减法和除法不满足交换律。例如,
3 − 8 = 不是整数
8 − 3 = 5
所以减法不满足交换律。
类似地,除法也不满足交换律。例如,
${4}/{8}$ = ${1}/{2}$
${8}/{4}$ = 2
结合律和分配律
结合律
当三个或更多整数相加或相乘时,无论数字的组合方式如何,结果都保持不变。这称为整数的结合律。
整数的加法和乘法满足结合律。
示例
8 + (4 + 2) = 8 + 6 = 14
(8 + 4) + 2 = 12 + 2 = 14
类似地,
8 × (4 × 2) = 8 × 8 = 64
(8 × 4) × 2 = 32 × 2 = 64
如果用不同的分组方式对相同的数字进行减法,我们将得到不同的结果。
8 − (4 − 2) = 8 − 2 = 6
(8 − 4) − 2 = 4 − 2 = 2
类似地,除法也不满足结合律。
8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4
(8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1
整数的减法和除法不满足结合律。
分配律
让我们来看表达式
8 × (4 + 2)
首先,计算括号内的数字。所以,我们得到,
8 × (4 + 2) = 8 × 6 = 48
同一个表达式也可以计算为,
8 × (4 + 2)
= (8 × 4) + (8 × 2)
= 32 + 16 = 48
在两种情况下,我们都得到相同的结果。
在第二种方法中,括号外的数字(8)分别乘以括号内的每个数字(4和2),然后将这些乘积加起来得到最终答案。
这种将乘法分配到括号内所有数字的性质称为分配律。
单位元
考虑以下情况
2 + 0 = 2
5 + 0 = 5
任何数 + 0 = 同一个数
这称为整数的加法单位元。所以,0是整数加法的单位元。
对于不同的运算,例如加法、减法、乘法和除法,单位元可能不同。
任何数 + 0 = 同一个数
任何数 − 0 = 同一个数
任何数 × 1 = 同一个数
任何数 ÷ 1 = 同一个数
1是整数乘法和除法的单位元。
使用整数的模式
我们可以使用整数创建不同的模式,例如直线、三角形、正方形和矩形。
假设一个点表示数字1,两个点表示数字2,以此类推。我们可以用给定的点集创建不同的模式。
用1个点,我们无法创建任何模式。它始终保持一个点。
直线
如果给出两个点,则这两个点可以连接在一起形成一条直线。

再加一个点,我们仍然可以形成一条直线。

我们可以用任意数量的点形成一条直线,除了1个点。
三角形数
构成三角形的数字称为三角形数。例如,3、6、10、15和21是三角形数。
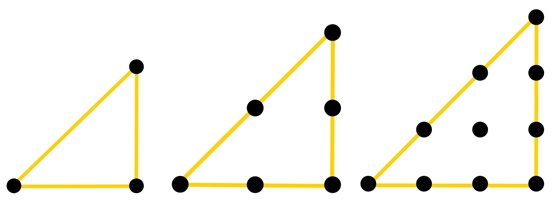
平方数
我们将一个整数乘以自身得到一个平方数。4、9、16……是构成正方形图案的数字。
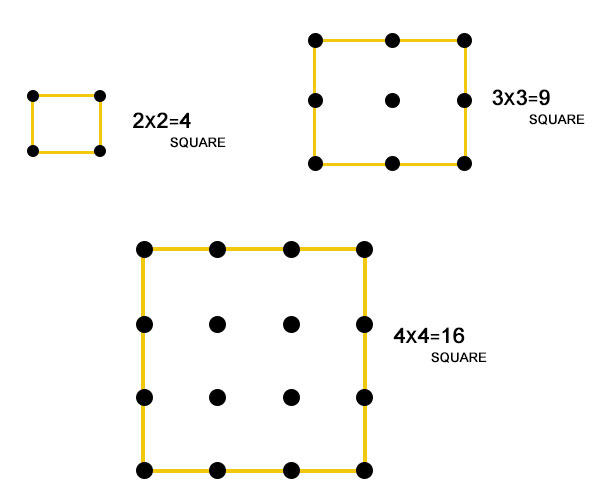
如果我们将任意两个连续的三角形数相加,最终会得到一个平方数。例如,
3 + 6 = 9
6 + 10 = 16
10 + 15 = 25
6和10是连续的三角形数,而16是一个平方数。
矩形数
可以排列成矩形图案的整数称为矩形数
如果一个整数可以写成两个不同整数的乘积(其中一个整数不应为1),则它是一个矩形数。
示例:12是一个矩形数,因为它可以表示为,
2 × 6 = 12
3 × 4 = 12
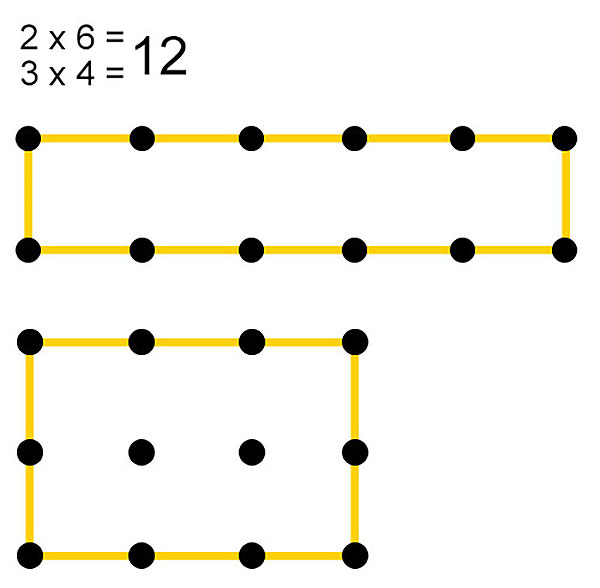
所有平方数都是矩形数,但反之则不然。
你知道BODMAS吗?
什么是BODMAS?
要计算包含多个运算的表达式,我们需要根据其定义的优先级级别执行运算。
- (B)rackets(括号)具有最高优先级
- (O)rder(次序)具有下一个优先级
- (D)ivision(除法)具有下一个优先级,然后是
- (M)ultiplication(乘法),然后是
- (A)ddition(加法),最后是
- (S)ubtraction(减法)。
这些单词的首字母组合在一起形成BODMAS。
示例
Question: Evaluate the following numerical expression:
3 + 9 × 6 − 22 ÷ 2 + (100 ÷ 2)
Solution: This expression has multiple arithmetic operations like addition, subtraction, multiplication, and division.
First priority; evaluate the numbers inside the brackets.
100 ÷ 2 = 50
The next priority is division, which gives us,
22 ÷ 2 = 11
Our expression now reduces to,
3 + 9 × 6 − 11 + 50
Performing multiplication next, we get,
9 × 6 = 54
The expression now becomes,
3 + 54 − 11 + 50
Next priority is addition. So, we add,
3 + 54 + 50 = 107
Last priority is subtraction. So,
107 − 11 = 96
示例
Question: Evaluate the expression (16 + 3 × 5) − 7 × 3 + 6.
Solution: First priority: Brackets,
16 + 3 × 5 = 16 + 15 = 31
Next priority: Division: No operation
Next priority: Multiplication,
7 × 3 = 21
The expression has now become,
31 − 21 + 6
Next priority: Addition,
31 + 6 = 37
Last priority: Subtraction,
37 − 21 = 16
To conclude,
(16 + 3 × 5) − 7 × 3 + 6 = 16