
第13章 - 对称
对称的介绍
对称广泛应用于几何学和建筑学的研究。从数学角度来说,对称意味着一个形状在某种移动方式下(旋转、翻转或滑动)可以完全与另一个形状重合。
对称物体
当一个图像或物体被分成两个相等的半部分,其中一半是另一半的复制品时,我们可以说该图像或物体是对称的。例如:
非对称物体
不显示对称性的物体称为非对称物体。例如:

对称轴
将二维物体分成镜像两半的直线称为该物体的对称轴。一个物体可以有多条对称轴。例如:
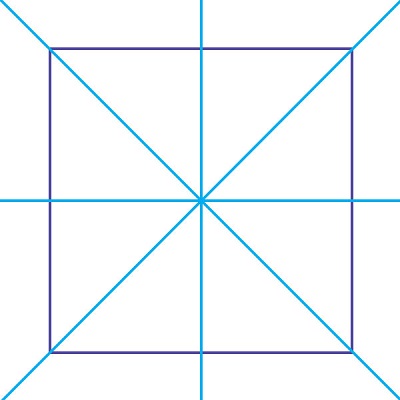
对称轴
将二维物体分成镜像两半的直线称为对称轴。对称轴不依赖于方向。它可以是垂直的、水平的或倾斜的。
对称物体可以有多条对称轴。非对称物体没有对称轴。
1条对称轴
如果只有一个直线可以将物体分成两半,则该物体具有1条对称轴。

2条对称轴
如果有两条直线可以将物体分成两半,则该物体具有2条对称轴。
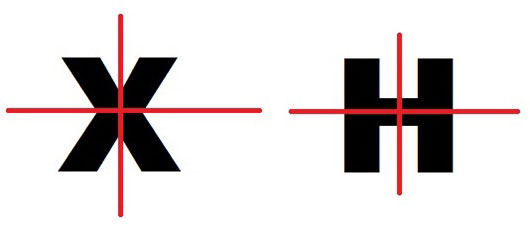
3条对称轴
如果有三条直线可以将物体分成两半,则该物体具有3条对称轴。
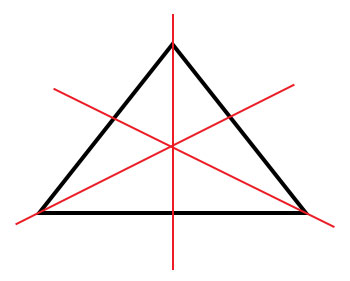
无限条对称轴
如果有无限条直线可以将物体分成两半,则该物体具有无限条对称轴。
反射与对称
物体及其镜像
当物体放置在镜子前时,会在镜子上形成其镜像。镜像具有相同的高度、宽度和角度。
然而,物体和它的镜像之间存在差异。也就是说,物体的左边变成了镜像的右边,反之亦然。
例如,当我们在镜子前举起左手时,我们在镜像中看到的是右手举起。这种现象也被称为**左右反转**。
反射与对称
原始物体及其镜像彼此对称,因此镜子充当对称轴。
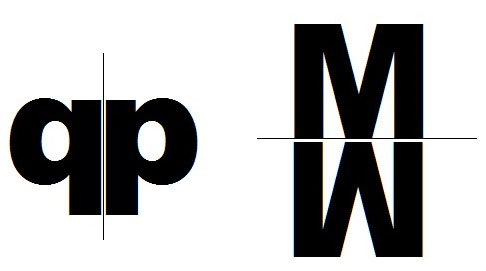
对称的应用
对称具有广泛的应用。它在增强物体的美感方面起着重要作用。
Rangoli(印度传统彩绘)
对称的广泛应用之一是Rangoli。使用对称图案制作的Rangoli,会产生美丽的图案。

Rangoli可以有多条对称轴,这增加了它们的美感。
纺织品
我们还可以在各种纺织品中看到对称性。一些服装嵌入了各种对称图案以增强其美感。

更多的对称轴会产生更美丽的艺术作品。
纪念碑
世界上许多著名的建筑和纪念碑都是利用各种形式的对称性进行设计的。一些著名的例子包括泰姬陵、埃菲尔铁塔、卢浮宫等。

很明显,对称物体比非对称物体看起来更美。
制作对称图案
我们可以用简单的方法创建对称图案。
墨迹魔鬼
可以使用墨迹在纸上绘制漂亮的对称图案。此过程称为墨迹魔鬼。
- 取一张纸,对折。
- 在一侧滴几滴墨水,然后将两半压在一起。
- 然后,展开纸张以查看对称图案。
它的**对称轴**将是纸张对折的直线。
根据图像的类型,可能存在一条或多条对称轴。

纸张对称
有一种简单的方法可以在纸上绘制对称图形。
- 取一张纸,对折。
- 在纸张边缘绘制一个形状。
- 沿着图案剪开纸张。
现在,打开纸张以查看对称图形。

万花筒
这是一种圆柱形装置,带有镜子,里面包含不同颜色的物体,例如鹅卵石和玻璃碎片。当我们从一端观看时,进入另一侧的光线由于镜子的反射而产生彩色的图案。
