
第7章 - 分数
分数介绍
分数用两个数字表示,一个在上,一个在下,用分隔线隔开。
分数、分子、分母
当一个整体被分成相等的部分时,这些部分用分数表示。在一个分数中,
- 写在上面的数字称为分子,并且
- 写在下面的数字称为分母。
整体被分成相等部分的总数由分母表示,而选择的相同部分的个数由分子表示。
例如,如果一个图形被分成5个相等的部分,其中选择了3个,那么选择的部分是${3}/{5}$。
问题
在一条四车道高速公路上,如果有3条车道是给汽车使用的,1条车道是给自行车使用的,那么表示汽车和自行车的分数是多少?
解答
有3条车道是给汽车使用的。所以,表示汽车的分数 = ${3}/{4}$ 只有一条车道是给自行车使用的。所以,表示自行车的分数 = ${1}/{4}$问题
一个披萨被分成6个相等的部分。这个披萨平均分给2个朋友。每个朋友得到多少披萨?如果这个披萨平均分给3个朋友,每个朋友得到多少披萨?
解答
总份数 = 6 6份披萨平均分给2个朋友。那么,他们每个人得到${6}/{2}$ = 3份 所以每个朋友得到的披萨分数 = ${3}/{6}$ 如果披萨分给3个朋友,那么他们每个人将得到2份。每个朋友得到的披萨分数 = ${2}/{6}$问题
在一所学校里,举行了一场100米赛跑。杰克、山姆和吉尔参加了比赛。杰克跑了50米,山姆跑了90米,吉尔完成了比赛并获胜。
- 他们每个人跑的距离占总距离的几分之几?
- 完成比赛的学生占总学生数的几分之几?
- 没有完成比赛的学生占总学生数的几分之几?
解答
总距离 = 100米 杰克跑的距离分数 $$ = {杰克跑的距离}/{总距离} = {50}/{100} = {1}/{2}$$ 山姆跑的距离分数 $$ = {山姆跑的距离}/{总距离} = {90}/{100} = {9}/{10}$$ 吉尔跑的距离分数 $$ = {吉尔跑的距离}/{总距离} = {100}/{100} = {1}/{1}$$ 在三个学生中,只有吉尔完成了比赛。所以,完成比赛的学生分数 = ${1}/{3}$ 而没有完成比赛的学生分数 = ${2}/{3}$分数的类型
根据分子是否大于分母,分数可以分为两种类型。
真分数
分子小于分母的分数称为真分数。这些分数的值小于1。
例如,${2}/{3}$,${6}/{23}$,${34}/{213}$等等。
假分数
分子大于分母的分数称为假分数。这些分数的值大于1。
例如,${3}/{2}$,${21}/{12}$,${544}/{213}$等等。
带分数
由于假分数大于1,它们可以写成整数和分数的组合。例如,
$${11}/{4} = 2 \: 和 \: {3}/{4} = 2{3}/{4}$$
分子和分母相等的分数表示一个整体。
这种既有整数部分又有分数部分的分数(或数字)称为带分数(或带分数)。
带分数可以转换为假分数,反之亦然。
分数的转换
假分数和带分数是同一数量的两种不同表示方法。
带分数
带分数是表示假分数的另一种方法。它们是由一个整数和一个真分数组成的数。
假分数转换为带分数
要将假分数转换为带分数,可以使用除法运算。
- 首先用分母去除分子。
- 商成为整数部分。
- 余数成为分数的分子,分母保持不变。
问题
将${65}/{7}$转换为带分数。
解答
${65}/{7}$是一个假分数,因为分子大于分母。用7除65,65 ÷ 7 = 9(余数2)我们可以将65写成:65 = (7 × 9) + 2 所以,${65}/{7}$的带分数形式是9${2}/{7}$。带分数转换为假分数
要将带分数转换为假分数,
- 首先将整数部分与分母相乘。
- 将乘积加到分子上。这就是假分数的分子。
- 分母保持不变。
问题
将4${7}/{9}$转换为假分数。
解答
将整数部分与分母相乘。4 × 9 = 36 将乘积与分子相加。36 + 7 = 43 分母保持不变。所以,4${7}/{9}$的假分数是${43}/{9}$。数轴上分数的表示
就像整数一样,分数也可以在数轴上表示。
数轴上真分数的表示
- 由于真分数是整体的一部分,因此表示需要将整体分成相等的部分。
- 部分的数量取决于分数的分母。
- 所以0和1之间的间隔被分成与分母相同数量的相等部分。
- 然后确定真分数的分子。
- 等于分子值的部分等于真分数。
问题
在数轴上表示真分数${3}/{7}$。
解答
分数的分母 = 7 所以,将0和1之间的间隔分成七个相等的部分。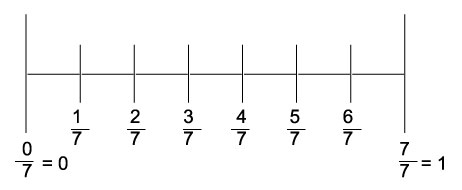
等于分子值(即3)的部分等于真分数。所以,分数${3}/{7}$可以表示如下
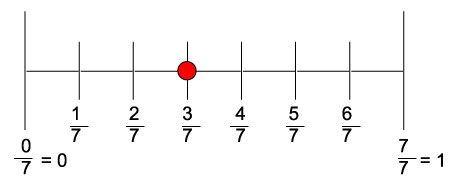
数轴上假分数的表示
带分数是在两个整数之间的一个数。换句话说,它是一个整数和一个整体的一部分。
要表示假分数,
- 首先将假分数转换为带分数。
- 在带分数中,整数部分表示该数后面的整数。
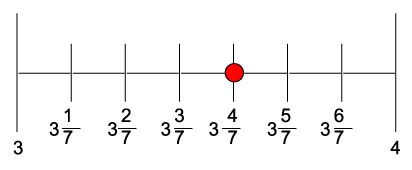
例子:在数轴上表示分数3${4}/{7}$。
解答:
3${4}/{7}$将位于整数3和4之间。

接下来,将间隔分成七个相等的部分(与分母相同)。
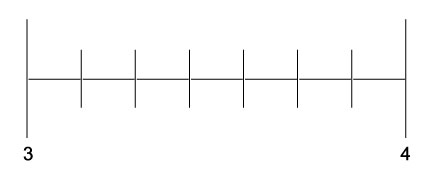
它们被编号为
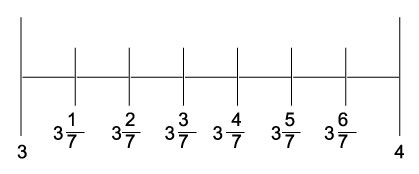
所以,3${4}/{7}$将是3个整体和3和4之间整体的第4部分。
等值分数
等值分数看起来不同,但它们的值相同或表示相同的数量。
例如,${2}/{4}$和${3}/{6}$在数轴上表示相同的点。它们是等值分数。
同样,${3}/{7}$,${6}/{14}$,${9}/{21}$……是等值分数,它们都表示相同的数量${3}/{7}$。
寻找等值分数
要找到给定分数的等值分数,将原分数的分子和分母乘以或除以相同的数。
例子:找出${1}/{4}$的等值分数
解答:
${1}/{4}$的一些等值形式是
- ${1 × 2}/{4 × 2}$ = ${2}/{8}$
- ${1 × 3}/{4 × 3}$ = ${3}/{12}$
- ${1 × 4}/{4 × 4}$ = ${4}/{16}$
- ${1 × 5}/{4 × 5}$ = ${5}/{20}$
例子:找出${3}/{8}$的等值分数
解答:
${3}/{8}$的一些等值形式是
- ${3 × 2}/{8 × 2}$ = ${6}/{16}$
- ${3 × 3}/{8 × 3}$ = ${9}/{24}$
- ${3 × 4}/{8 × 4}$ = ${12}/{32}$
- ${3 × 5}/{8 × 5}$ = ${15}/{40}$
分数的简化
分数${6}/{12}$可以用较大的数字表示为${100}/{200}$,也可以用较小的数字表示为${1}/{2}$。分数的简化是寻找分数最简等值形式的过程。
分数的最简形式定义为分子和分母除了1以外没有其他公因数的分数。例如,${2}/{3}$,${5}/{9}$,${23}/{97}$等等。
第一种方法
要找到分数的最简形式,可以通过用相同的数去除分子和分母来找到它的等值形式。
例子:简化分数${9}/{36}$。
解答:
由于9和36有公因数3,则一个简化形式为
$${9}/{36} = {9}/{3} \: / \: {36}/{3} = {3}/{12}$$
3和12有公因数3,所以将继续简化
$${3}/{12} = {3}/{3} \: / \: {12}/{3} = {1}/{4}$$
由于1和4除了1以外没有公因数,所以这是原分数的最简形式。
第二种方法
我们可以通过用两个数的最大公因数(HCF)去除分子和分母来找到分数的最简形式。
例子:简化分数${9}/{36}$
解答:
让我们找出数字9和36的最大公因数。

因此,9和36的最大公因数是9。
用最大公因数去除分子和分母,
$${9}/{36} = {9}/{9} \: / \: {36}/{9} = {1}/{4}$$
${1}/{4}$是最简形式的分数。
同分母分数和异分母分数
同分母分数
具有相同分母的分数称为同分母分数。例如,
$${2}/{7}, {5}/{7}, {14}/{7}, {236}/{7}$$
是同分母分数,因为它们具有相同的分母“7”。
异分母分数
具有不同分母的分数称为异分母分数。例如,
$${23}/{3}, {322}/{12}, {56}/{531}, {12}/{4}$$
是异分母分数,因为每个分数都有不同的分母。
例子:在一个生日聚会上,一个蛋糕被切成20个相等的部分。三个朋友分别得到5块、2块和1块。朋友们分别得到了多少蛋糕?
解答:
朋友们得到的蛋糕分数是${5}/{20}$,${2}/{20}$和${1}/{20}$。
这些是同分母分数。
例子:如果将前面例子中的分数,即${5}/{20}$,${2}/{20}$和${1}/{20}$简化为最简形式,则得到${1}/{4}$,${1}/{10}$和${1}/{20}$。这些是什么类型的分数?
解答:
分数${1}/{4}$,${1}/{10}$和${1}/{20}$的分母是不同的。
这些是异分母分数。
例子:将下列分数分类为同分母分数和异分母分数。
$${1}/{2}, {7}/{4}, {3}/{2}, {9}/{11}, {5}/{2}, {13}/{6}$$
解答:
在给定的分数中,
${1}/{2}$,${3}/{2}$,${5}/{2}$是同分母分数,因为它们具有相同的分母2。
${7}/{4}$,${9}/{11}$,${13}/{6}$是异分母分数,因为它们具有不同的分母。
分数的比较
同分母分数的比较
同分母分数的比较很简单,因为它们的分母相同。要比较两个同分母分数,只需比较它们的分子。
例:比较分数 ${2}/{7}$ 和 ${3}/{7}$
解答:
分数 ${2}/{7}$ 和 ${3}/{7}$ 有相同的分母。所以,由于 2 < 3,我们可以说 ${2}/{7}$ < ${3}/{7}$。
异分母分数的比较
要比较两个异分母分数,
- 首先将异分母分数转换为具有相同分母的等值同分母分数。
- 然后,比较等值分数的分子。
分数的分母通过乘法/除法转换为它们的最小公倍数 (LCM)。
相应的分子乘以相同的数字,从而得到具有相同分母的等值分数。
例:比较分数 ${2}/{3}$ 和 ${5}/{7}$
解答:
我们有两个异分母分数:${2}/{3}$ 和 ${5}/{7}$
让我们使用等值分数将它们转换为同分母分数。
两个分母 3 和 7 的最小公倍数 = 21。
因此,等值分数将具有 21 作为分母。
转换第一个分数
$${2 × 7}/{3 × 7} = {14}/{21}$$
转换第二个分数
$${5 × 3}/{7 × 3} = {15}/{21}$$
现在,比较等值同分母分数的分子。
由于 14 < 15,
$${14}/{21} < {15}/{21} \: 或 \: {2}/{3} < {5}/{7}$$
例:比较 ${4}/{5}$ 和 ${16}/{20}$
解答:
我们有两个异分母分数:${4}/{5}$ 和 ${16}/{20}$
分母 5 和 20 的最小公倍数 = 20
因此,等值分数将具有 20 作为分母。
转换第一个分数
$${4 × 4}/{5 × 4} = {16}/{20}$$
转换第二个分数
$${16 × 1}/{20 × 1} = {16}/{20}$$
现在,比较等值同分母分数的分子。
两个数字都具有相同的分子和分母,因此
$${4}/{5} = {16}/{20}$$
分数的加法和减法
同分母分数的加法和减法
分数的加法与整数的加法不同。在加或减同分母分数时,分母保持不变,分子相加或相减。
例:加分数 ${3}/{16}$ + ${7}/{16}$
解:在加同分母分数时,只需将分子相加,保持分母不变。
$${3}/{16} + {7}/{16} = {3 + 7}/{16} = {10}/{16}$$
例:减分数 ${8}/{19}$ − ${7}/{19}$
解:在减同分母分数时,只需将分子相减,保持分母不变。
$${8}/{19} − {7}/{19} = {8 − 7}/{19} = {1}/{19}$$
异分母分数的加法和减法
在加或减异分母分数时,
- 首先将它们转换为同分母分数,
- 然后将分子相加或相减,
- 分母保持不变。
例:加 ${3}/{8}$ + ${7}/{6}$
解答:
我们有两个异分母分数,
$${3}/{8} \: 和 \: {7}/{6}$$
让我们首先将它们转换为同分母分数。
分母 8 和 6 的最小公倍数 = 24
因此,公分母将是 24。
${3}/{8}$ 和 ${7}/{6}$ 的等值同分母分数是
$${3}/{8} = {(3 × 3)}/{(8 × 3)} = {9}/{24}$$
$${7}/{6} = {(7 × 4)}/{(6 × 4)} = {28}/{24}$$
将分子相加,保持分母不变。
$${3}/{8} + {7}/{6} = {9}/{24} + {28}/{24} = {37}/{24}$$
例:减 ${7}/{6}$ − ${3}/{8}$
解答:
6 和 8 的最小公倍数 = 24
公分母将是 24
减去它们的等值同分母分数,
$${7}/{6} − {3}/{8} = {(7 × 4)}/{(6 × 4)} − {(3 × 3)}/{(8 × 3)}$$
$$ = {28}/{24} − {9}/{24} = {28 − 9}/{24}$$
$$ = {19}/{24}$$
加法和减法的特殊情况
整数加真分数
任何整数除以 1 等于它本身。例如,
$${12}/{1} = 12 \: 和 \: {4}/{1} = 4$$
因此,任何整数都可以通过将其分母设为 1 来表示为分数。
例:加 9 + ${2}/{7}$
解答:
$$9 + {2}/{7} = {9}/{1} + {2}/{7}$$
但这些是异分母分数。
让我们将它们转换为同分母分数。
$${9}/{1} = {9 × 7}/{1 × 7} = {63}/{7}$$
同样地,
$${2}/{7} = {2 × 1}/{7 × 1} = {2}/{7}$$
现在加上同分母分数,
$${63}/{7} + {2}/{7} = {63 + 2}/{7} = {65}/{7}$$
将假分数转换为带分数,
$${65}/{7} = 9{2}/{7}$$
另一种方法
要加一个整数和一个真分数,去掉问题中的加号,将其写成带分数。例如,
$$9 + {2}/{7} = 9{2}/{7}$$
$$5 + {3}/{11} = 5{3}/{11}$$
整数减真分数
整数表示为分母为 1 的分数。
将异分母分数转换为同分母分数,然后相减以获得结果。
例:加 9 − ${2}/{7}$
解答:
$$9 − {2}/{7} = {9}/{1} − {2}/{7}$$
${9}/{1}$ 和 ${2}/{7}$ 的同分母分数是 ${63}/{7}$ 和 ${2}/{7}$
减去同分母分数,
$${63}/{7} − {2}/{7} = {63 − 2}/{7} = {61}/{7}$$
将假分数转换为带分数,
$${61}/{7} = 8{5}/{7}$$