作图：从半径为6厘米的同心圆上一点，作半径为4厘米的圆的切线，并测量其长度。还要通过实际计算验证测量结果。

已知：

两个同心圆的半径。

要求：

我们必须从半径为6厘米的同心圆上一点，作半径为4厘米的圆的切线。

解法

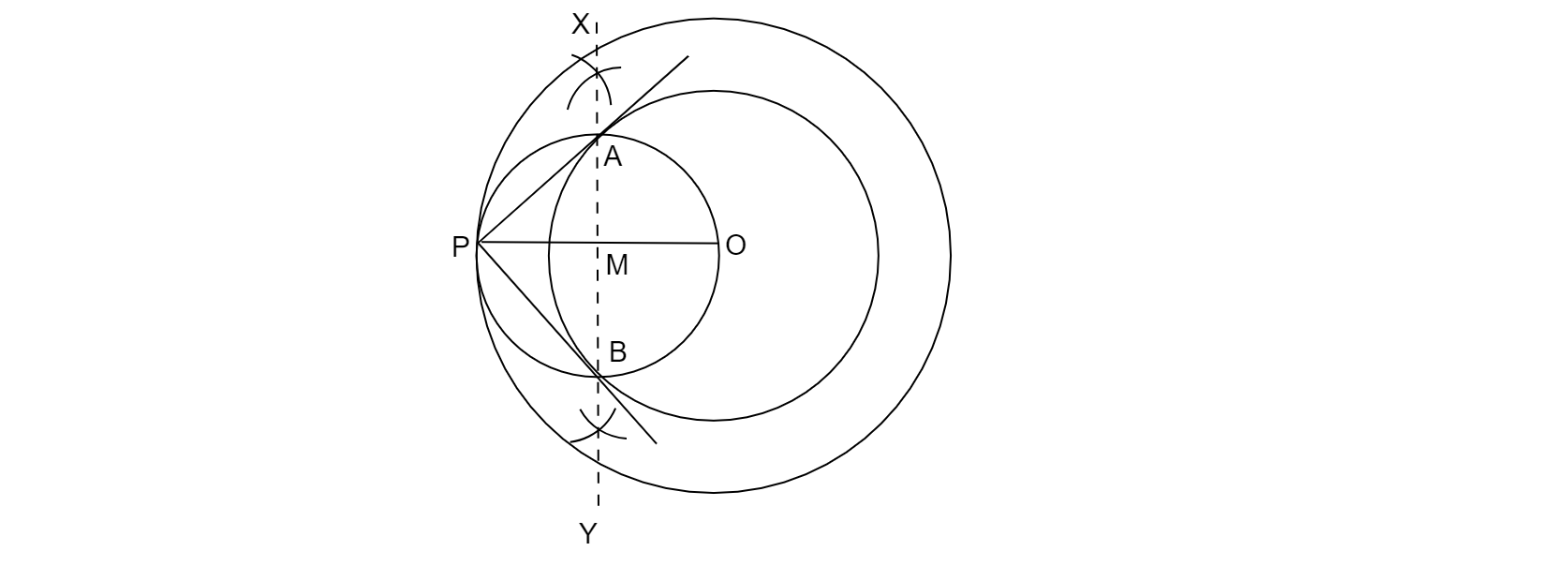
作图步骤

1. 画两个同心圆，圆心为O，半径分别为4厘米和6厘米。在外圆上取一点P，然后连接OP。

2. 作OP的垂直平分线。设平分线与OP相交于M。

3. 以M为圆心，OM为半径画一个圆。设它与内圆相交于A和B。

4. 连接PA和PB。

因此，PA和PB是所需的切线。

在△OAP中，

$OP^2=OA^2+AP^2$

$6^2=OA^2+4^2$

$OA^2=36-16$

$OA=\sqrt{20}$

$OA=2\sqrt{5}厘米$

同样地，

$OB=2\sqrt{5}厘米$

教程点

更新于：2022年10月10日

44 次浏览

开启你的职业生涯

完成课程获得认证

开始学习