凸优化 - 快速指南

---

---

凸优化 - 简介

本课程适用于希望解决各种工程和科学应用中出现的非线性优化问题的学生。本课程从线性规划的基本理论开始，将介绍凸集和凸函数的概念以及相关术语，以解释解决非线性规划问题所需的各种定理。本课程将介绍用于解决此类问题的各种算法。这些类型的问题出现在各种应用中，包括机器学习、电气工程中的优化问题等。它要求学生具备高中数学概念和微积分的预备知识。

在本课程中，学生将学习如何解决诸如 $min f\left ( x \right )$ 受某些约束条件的优化问题。

如果函数 $f\left ( x \right )$ 是线性函数，并且约束条件是线性的，则这些问题很容易解决。然后它被称为线性规划问题 $LPP$。但是，如果约束条件是非线性的，则很难解决上述问题。除非我们可以在图上绘制函数，然后尝试分析优化可能是一种方法，但如果函数超过三维，我们就无法绘制它。因此，出现了非线性规划或凸规划的技术来解决此类问题。在本教程中，我们将重点学习这些技术，最后介绍一些解决此类问题的算法。首先，我们将引入凸集的概念，它是凸规划问题的基础。然后，随着凸函数的引入，我们将介绍一些重要的定理来解决这些问题，以及基于这些定理的一些算法。

术语

• 空间 $\mathbb{R}^n$ - 它是一个具有实数的n维向量，定义如下 - $\mathbb{R}^n=\left \{ \left ( x_1,x_2,...,x_n \right )^{\tau }:x_1,x_2,....,x_n \in \mathbb{R} \right \}$

• 空间 $\mathbb{R}^{mXn}$ - 它是一组所有阶为 $mXn$ 的实值矩阵。

凸优化 - 线性规划

方法

线性规划也称为线性优化，是一种用于解决数学问题的技术，其中关系本质上是线性的。线性规划的基本性质是最大化或最小化目标函数，同时受某些约束条件的限制。目标函数是一个线性函数，它是从问题的数学模型中获得的。约束条件是强加于模型上的条件，并且也是线性的。

• 根据给定的问题，找到目标函数。
• 找到约束条件。
• 在图上绘制约束条件。
• 找到可行域，它是由所有约束条件的交集形成的。
• 找到可行域的顶点。
• 找到目标函数在这些顶点处的取值。
• 使目标函数最大化或最小化（根据问题）的顶点就是答案。

示例

步骤 1 - 最大化 $5x+3y$，受以下条件限制

$x+y\leq 2$，

$3x+y\leq 3$，

$x\geq 0 \:and \:y\geq 0$

解答 -

第一步是在图上找到可行域。

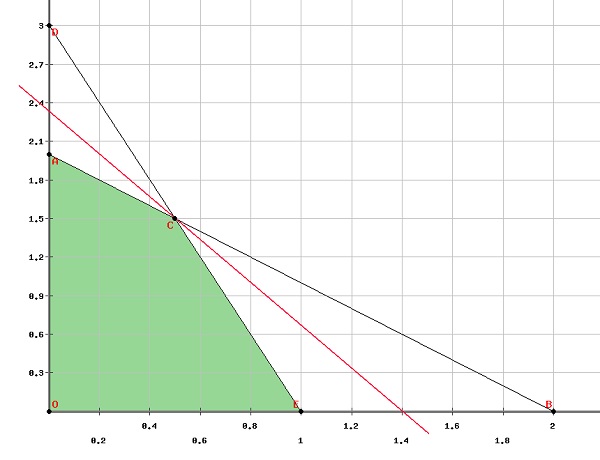
从图中可以清楚地看出，可行域的顶点是

$\left ( 0, 0 \right )\left ( 0, 2 \right )\left ( 1, 0 \right )\left ( \frac{1}{2}, \frac{3}{2} \right )$

令 $f\left ( x, y \right )=5x+3y$

将这些值代入目标函数，我们得到 -

$f\left ( 0, 0 \right )$=0

$f\left ( 0, 2 \right )$=6

$f\left ( 1, 0 \right )$=5

$f\left ( \frac{1}{2}, \frac{3}{2} \right )$=7

因此，函数在 $\left ( \frac{1}{2}, \frac{3}{2} \right )$ 处取得最大值。

步骤 2 - 一家手表公司生产电子表和机械表。长期预测表明，每天预计至少需要 100 块电子表和 80 块机械表。由于生产能力的限制，每天最多只能生产 200 块电子表和 170 块机械表。为了满足运输合同，每天必须运送至少 200 块手表。

如果每售出一块电子表就会造成 2 美元的损失，但每售出一块机械表就会产生 5 美元的利润，那么每天应该生产多少块每种类型的手表才能使净利润最大化？

解答 -

设 $x$ 为生产的电子表数量

$y$ 为生产的机械表数量

根据问题，每天至少要生产 100 块电子表，最多可以生产 200 块电子表。

$\Rightarrow 100 \leq \:x\leq 200$

同样，每天至少要生产 80 块机械表，最多可以生产 170 块机械表。

$\Rightarrow 80 \leq \:y\leq 170$

由于每天至少要生产 200 块手表。

$\Rightarrow x +y\leq 200$

由于每售出一块电子表就会造成 2 美元的损失，但每售出一块机械表就会产生 5 美元的利润，

总利润可以计算为

$利润 =-2x + 5y$

并且我们必须使利润最大化，因此，问题可以表述为 -

最大化 $-2x + 5y$，受以下条件限制

$100 \:\leq x\:\leq 200$

$80 \:\leq y\:\leq 170$

$x+y\:\leq 200$

将上述方程在图上绘制，我们得到，

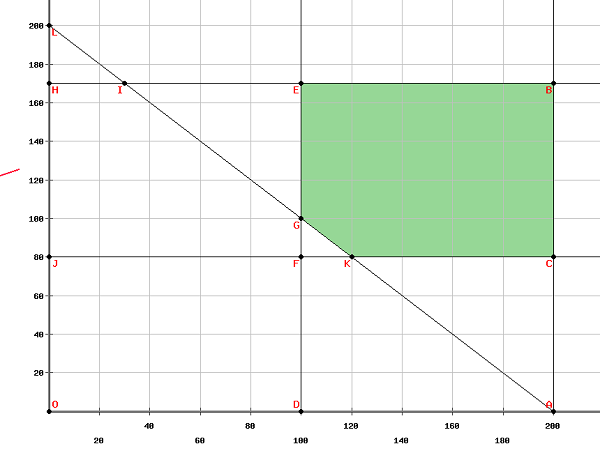
可行域的顶点是

$\left ( 100, 170\right )\left ( 200, 170\right )\left ( 200, 180\right )\left ( 120, 80\right ) and \left ( 100, 100\right )$

目标函数的最大值在 $\left ( 100, 170\right )$ 处获得。因此，为了使净利润最大化，应该生产 100 个电子表和 170 个机械表。

凸优化 - 范数

范数是一个函数，它为向量或变量赋予严格的正值。

范数是一个函数 $f:\mathbb{R}^n\rightarrow \mathbb{R}$

范数的基本特征是 -

设 $X$ 为一个向量，使得 $X\in \mathbb{R}^n$

• $\left \| x \right \|\geq 0$

• $\left \| x \right \|= 0 \Leftrightarrow x= 0\forall x \in X$

• $\left \|\alpha x \right \|=\left | \alpha \right |\left \| x \right \|\forall \:x \in X and \:\alpha \:is \:a \:scalar$

• $\left \| x+y \right \|\leq \left \| x \right \|+\left \| y \right \| \forall x,y \in X$

• $\left \| x-y \right \|\geq \left \| \left \| x \right \|-\left \| y \right \| \right \|$

根据定义，范数计算如下 -

• $\left \| x \right \|_1=\displaystyle\sum\limits_{i=1}^n\left | x_i \right |$

• $\left \| x \right \|_2=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^2 \right )^{\frac{1}{2}}$

• $\left \| x \right \|_p=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^p \right )^{\frac{1}{p}},1 \leq p \leq \infty$

范数是一个连续函数。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

证明

根据定义，如果 $x_n\rightarrow x$ in $X\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right )$ 则 $f\left ( x \right )$ 是一个常数函数。

令 $f\left ( x \right )=\left \| x \right \|$

因此，$\left | f\left ( x_n \right )-f\left ( x \right ) \right |=\left | \left \| x_n \right \| -\left \| x \right \|\right |\leq \left | \left | x_n-x \right | \:\right |$

由于 $x_n \rightarrow x$，因此 $\left \| x_n-x \right \|\rightarrow 0$

因此 $\left | f\left ( x_n \right )-f\left ( x \right ) \right |\leq 0\Rightarrow \left | f\left ( x_n \right )-f\left ( x \right ) \right |=0\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right )$

因此，范数是一个连续函数。

凸优化 - 内积

内积是一个函数，它为一对向量赋予一个标量。

内积 - $f:\mathbb{R}^n \times \mathbb{R}^n\rightarrow \kappa$，其中 $\kappa$ 是一个标量。

内积的基本特征如下 -

设 $X \in \mathbb{R}^n$

• $\left \langle x,x \right \rangle\geq 0, \forall x \in X$

• $\left \langle x,x \right \rangle=0\Leftrightarrow x=0, \forall x \in X$

• $\left \langle \alpha x,y \right \rangle=\alpha \left \langle x,y \right \rangle,\forall \alpha \in \kappa \: and\: \forall x,y \in X$

• $\left \langle x+y,z \right \rangle =\left \langle x,z \right \rangle +\left \langle y,z \right \rangle, \forall x,y,z \in X$

• $\left \langle \overline{y,x} \right \rangle=\left ( x,y \right ), \forall x, y \in X$

注意 -

• 范数和内积之间的关系：$\left \| x \right \|=\sqrt{\left ( x,x \right )}$

• $\forall x,y \in \mathbb{R}^n,\left \langle x,y \right \rangle=x_1y_1+x_2y_2+...+x_ny_n$

示例

1. 找到 $x=\left ( 1,2,1 \right )\: and \: y=\left ( 3,-1,3 \right )$ 的内积。

解答

$\left \langle x,y \right \rangle =x_1y_1+x_2y_2+x_3y_3$

$\left \langle x,y \right \rangle=\left ( 1\times3 \right )+\left ( 2\times-1 \right )+\left ( 1\times3 \right )$

$\left \langle x,y \right \rangle=3+\left ( -2 \right )+3$

$\left \langle x,y \right \rangle=4$

2. 若 $x=\left ( 4,9,1 \right ),y=\left ( -3,5,1 \right )$ 且 $z=\left ( 2,4,1 \right )$，求 $\left ( x+y,z \right )$

解答

我们知道，$\left \langle x+y,z \right \rangle=\left \langle x,z \right \rangle+\left \langle y,z \right \rangle$

$\left \langle x+y,z \right \rangle=\left ( x_1z_1+x_2z_2+x_3z_3 \right )+\left ( y_1z_1+y_2z_2+y_3z_3 \right )$

$\left \langle x+y,z \right \rangle=\left \{ \left ( 4\times 2 \right )+\left ( 9\times 4 \right )+\left ( 1\times1 \right ) \right \}+$

$\left \{ \left ( -3\times2 \right )+\left ( 5\times4 \right )+\left ( 1\times 1\right ) \right \}$

$\left \langle x+y,z \right \rangle=\left ( 8+36+1 \right )+\left ( -6+20+1 \right )$

$\left \langle x+y,z \right \rangle=45+15$

$\left \langle x+y,z \right \rangle=60$

凸优化 - 极小值和极大值

局部极小值或极小点

$\bar{x}\in \:S$ 被称为函数 $f$ 的局部极小值，如果 $f\left ( \bar{x} \right )\leq f\left ( x \right ),\forall x \in N_\varepsilon \left ( \bar{x} \right )$，其中 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\bar{x}$ 的邻域，即 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\left \| x-\bar{x} \right \|< \varepsilon$

局部极大值或极大点

$\bar{x}\in \:S$ 被称为函数 $f$ 的局部极大值，如果 $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \bar{x} \right )$，其中 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\bar{x}$ 的邻域，即 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\left \| x-\bar{x} \right \|< \varepsilon$

全局极小值

$\bar{x}\in \:S$ 被称为函数 $f$ 的全局极小值，如果 $f\left ( \bar{x} \right )\leq f\left ( x \right ), \forall x \in S$

全局极大值

$\bar{x}\in \:S$ 被称为函数 $f$ 的全局极大值，如果 $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in S$

示例

步骤 1 - 求 $f\left ( \bar{x} \right )=\left | x^2-4 \right |$ 的局部极小值和极大值

解答 -

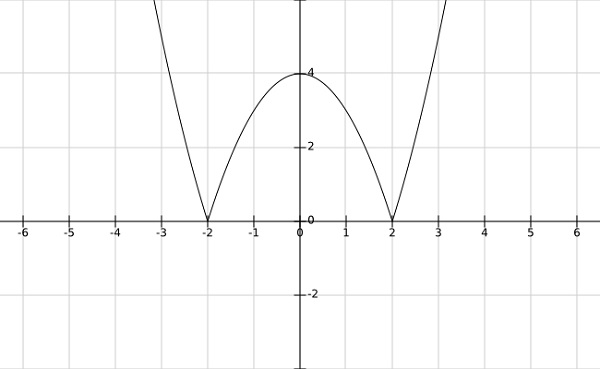
从上述函数的图像可以看出，局部极小值出现在 $x= \pm 2$ 处，局部极大值出现在 $x = 0$ 处。

步骤 2 - 求函数 $f\left (x \right )=\left | 4x^3-3x^2+7 \right |$ 的全局极小值

解答 -

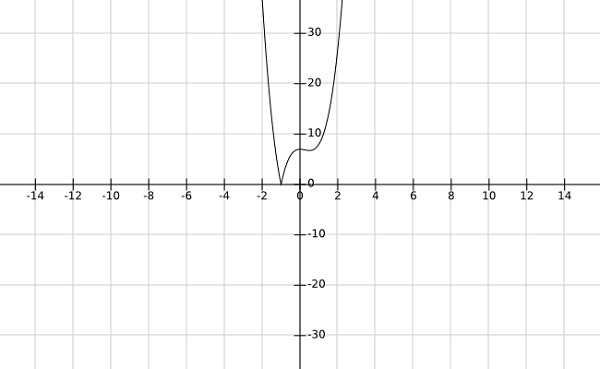
从上述函数的图像可以看出，全局极小值出现在 $x=-1$ 处。

凸优化 - 凸集

设 $S\subseteq \mathbb{R}^n$，如果集合 S 中任意两点的连线段也属于 S，则称集合 S 为凸集，即如果 $x_1,x_2 \in S$，则 $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S$，其中 $\lambda \in\left ( 0,1 \right )$。

注意 -

• 两个凸集的并集可能是凸集也可能不是凸集。
• 两个凸集的交集总是凸集。

证明

设 $S_1$ 和 $S_2$ 为两个凸集。

设 $S_3=S_1 \cap S_2$

设 $x_1,x_2 \in S_3$

由于 $S_3=S_1 \cap S_2$，因此 $x_1,x_2 \in S_1$ 且 $x_1,x_2 \in S_2$

由于 $S_i$ 是凸集，$\forall$ $i \in 1,2,$

因此 $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_i$，其中 $\lambda \in \left ( 0,1 \right )$

所以，$\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_1\cap S_2$

$\Rightarrow \lambda x_1+\left ( 1-\lambda \right )x_2 \in S_3$

因此，$S_3$ 是一个凸集。

• 形式为 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ 的加权平均，其中 $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ 且 $\lambda_i\geq 0,\forall i \in \left [ 1,k \right ]$，称为 $x_1,x_2,....x_k$ 的锥组合。

• 形式为 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ 的加权平均，其中 $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$，称为 $x_1,x_2,....x_k$ 的仿射组合。

• 形式为 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ 的加权平均，称为 $x_1,x_2,....x_k$ 的线性组合。

示例

步骤 1 - 证明集合 $S=\left \{ x \in \mathbb{R}^n:Cx\leq \alpha \right \}$ 是一个凸集。

解答

设 $x_1$ 和 $x_2 \in S$

$\Rightarrow Cx_1\leq \alpha$ 且 $\:Cx_2\leq \alpha$

要证明：$\:\:y=\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\in S \:\forall \:\lambda \in\left ( 0,1 \right )$

$Cy=C\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=\lambda Cx_1+\left ( 1-\lambda \right )Cx_2$

$\Rightarrow Cy\leq \lambda \alpha+\left ( 1-\lambda \right )\alpha$

$\Rightarrow Cy\leq \alpha$

$\Rightarrow y\in S$

因此，$S$ 是一个凸集。

步骤 2 - 证明集合 $S=\left \{ \left ( x_1,x_2 \right )\in \mathbb{R}^2:x_{1}^{2}\leq 8x_2 \right \}$ 是一个凸集。

解答

设 $x,y \in S$

设 $x=\left ( x_1,x_2 \right )$ 且 $y=\left ( y_1,y_2 \right )$

$\Rightarrow x_{1}^{2}\leq 8x_2$ 且 $y_{1}^{2}\leq 8y_2$

要证明 - $\lambda x+\left ( 1-\lambda \right )y\in S\Rightarrow \lambda \left ( x_1,x_2 \right )+\left (1-\lambda \right )\left ( y_1,y_2 \right ) \in S\Rightarrow \left [ \lambda x_1+\left ( 1- \lambda)y_2] \in S\right ) \right ]$

$现在， \left [\lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}=\lambda ^2x_{1}^{2}+\left ( 1-\lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1-\lambda \right )x_1y_1$

但是 $2x_1y_1\leq x_{1}^{2}+y_{1}^{2}$

因此，

$\left [ \lambda x_1 +\left ( 1-\lambda \right )y_1\right ]^{2}\leq \lambda ^2x_{1}^{2}+\left ( 1- \lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1- \lambda \right )\left ( x_{1}^{2}+y_{1}^{2} \right )$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq \lambda x_{1}^{2}+\left ( 1- \lambda \right )y_{1}^{2}$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\lambda x_2+8\left ( 1- \lambda \right )y_2$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\left [\lambda x_2+\left ( 1- \lambda \right )y_2 \right ]$

$\Rightarrow \lambda x+\left ( 1- \lambda \right )y \in S$

步骤 3 - 证明集合 $S \in \mathbb{R}^n$ 是凸集当且仅当对于每个整数 k，S 的任意 k 个点的任意凸组合都在 S 中。

解答

设 S 为凸集。然后，要证明；

$c_1x_1+c_2x_2+.....+c_kx_k \in S, \displaystyle\sum\limits_{1}^k c_i=1,c_i\geq 0, \forall i \in 1,2,....,k$

用数学归纳法证明

对于 $k=1,x_1 \in S, c_1=1 \Rightarrow c_1x_1 \in S$

对于 $k=2,x_1,x_2 \in S, c_1+c_2=1$ 并且由于 S 是凸集

$\Rightarrow c_1x_1+c_2x_2 \in S.$

假设 S 的 m 个点的凸组合在 S 中，即

$c_1x_1+c_2x_2+...+c_mx_m \in S,\displaystyle\sum\limits_{1}^m c_i=1 ,c_i \geq 0, \forall i \in 1,2,...,m$

现在，设 $x_1,x_2....,x_m,x_{m+1} \in S$

设 $x=\mu_1x_1+\mu_2x_2+...+\mu_mx_m+\mu_{m+1}x_{m+1}$

设 $x=\left ( \mu_1+\mu_2+...+\mu_m \right )\frac{\mu_1x_1+\mu_2x_2+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}+\mu_{m+1}x_{m+1}$

设 $y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}$

$\Rightarrow x=\left ( \mu_1+\mu_2+...+\mu_m \right )y+\mu_{m+1}x_{m+1}$

现在 $y \in S$，因为系数之和为 1。

$\Rightarrow x \in S$，因为 S 是凸集且 $y,x_{m+1} \in S$

因此，用数学归纳法证明。

凸优化 - 仿射集

如果对于任意两点，经过这两点的直线都位于集合 A 中，则称集合 A 为仿射集。

注意 -

• $S$ 是仿射集当且仅当它包含其所有点的仿射组合。

• 空集和单点集都是仿射集和凸集。

  例如，线性方程的解集是仿射集。

证明

设 S 为线性方程的解集。

根据定义，$S=\left \{ x \in \mathbb{R}^n:Ax=b \right \}$

设 $x_1,x_2 \in S\Rightarrow Ax_1=b$ 且 $Ax_2=b$

要证明 : $A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=b, \forall \theta \in\left ( 0,1 \right )$

$A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=\theta Ax_1+\left ( 1-\theta \right )Ax_2=\theta b+\left ( 1-\theta \right )b=b$

因此 S 是仿射集。

定理

如果 C 是仿射集且 $x_0 \in C$，则集合 $V= C-x_0=\left \{ x-x_0:x \in C \right \}$ 是 C 的子空间。

证明

设 $x_1,x_2 \in V$

要证明：$\alpha x_1+\beta x_2 \in V$，对于某些 $\alpha,\beta$

现在，$x_1+x_0 \in C$ 且 $x_2+x_0 \in C$，根据 V 的定义

现在，$\alpha x_1+\beta x_2+x_0=\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0$

但是 $\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0 \in C$，因为 C 是仿射集。

因此，$\alpha x_1+\beta x_2 \in V$

因此得证。

凸优化 - 包

S 中一组点的凸包是包含 S 中所有点（在其内部或边界上）的最小凸区域的边界。

或

设 $S\subseteq \mathbb{R}^n$，S 的凸包，记为 $Co\left ( S \right )$，是 S 的所有凸组合的集合，即 $x \in Co\left ( S \right )$ 当且仅当 $x \in \displaystyle\sum\limits_{i=1}^n \lambda_ix_i$，其中 $\displaystyle\sum\limits_{1}^n \lambda_i=1$ 且 $\lambda_i \geq 0 \forall x_i \in S$

备注 - S 中一组点的凸包在平面上定义了一个凸多边形，S 中位于多边形边界上的点定义了多边形的顶点。

定理 $Co\left ( S \right )= \left \{ x:x=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i,x_i \in S, \displaystyle\sum\limits_{i=1}^n \lambda_i=1,\lambda_i \geq 0 \right \}$ 证明凸包是凸集。

证明

设 $x_1,x_2 \in Co\left ( S \right )$，则 $x_1=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i$ 且 $x_2=\displaystyle\sum\limits_{i=1}^n \lambda_\gamma x_i$，其中 $\displaystyle\sum\limits_{i=1}^n \lambda_i=1, \lambda_i\geq 0$ 且 $\displaystyle\sum\limits_{i=1}^n \gamma_i=1,\gamma_i\geq0$

对于 $\theta \in \left ( 0,1 \right ),\theta x_1+\left ( 1-\theta \right )x_2=\theta \displaystyle\sum\limits_{i=1}^n \lambda_ix_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n \gamma_ix_i$

$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n \lambda_i \theta x_i+\displaystyle\sum\limits_{i=1}^n \gamma_i\left ( 1-\theta \right )x_i$

$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]x_i$

考虑系数，

$\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]=\theta \displaystyle\sum\limits_{i=1}^n \lambda_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n\gamma_i=\theta +\left ( 1-\theta \right )=1$

因此，$\theta x_1+\left ( 1-\theta \right )x_2 \in Co\left ( S \right )$

因此，凸包是凸集。

Caratheodory定理

设 S 为 $\mathbb{R}^n$ 中的任意集合。如果 $x \in Co\left ( S \right )$，则 $x \in Co\left ( x_1,x_2,....,x_n,x_{n+1} \right )$.

证明

由于 $x \in Co\left ( S\right )$，则 x 可以表示为 S 中有限多个点的凸组合，即

$x=\displaystyle\sum\limits_{j=1}^k \lambda_jx_j,\displaystyle\sum\limits_{j=1}^k \lambda_j=1, \lambda_j \geq 0$ 且 $x_j \in S, \forall j \in \left ( 1,k \right )$

如果 $k \leq n+1$，则显然结果成立。

如果 $k \geq n+1$，则 $\left ( x_2-x_1 \right )\left ( x_3-x_1 \right ),....., \left ( x_k-x_1 \right )$ 线性相关。

$\Rightarrow \exists \mu _j \in \mathbb{R}, 2\leq j\leq k$（不全为零）使得 $\displaystyle\sum\limits_{j=2}^k \mu _j\left ( x_j-x_1 \right )=0$

定义 $\mu_1=-\displaystyle\sum\limits_{j=2}^k \mu _j$，则 $\displaystyle\sum\limits_{j=1}^k \mu_j x_j=0, \displaystyle\sum\limits_{j=1}^k \mu_j=0$

其中不全 $\mu_j$ 等于零。由于 $\displaystyle\sum\limits_{j=1}^k \mu_j=0$，因此至少有一个 $\mu_j > 0,1 \leq j \leq k$

然后，$x=\displaystyle\sum\limits_{1}^k \lambda_j x_j+0$

$x=\displaystyle\sum\limits_{1}^k \lambda_j x_j- \alpha \displaystyle\sum\limits_{1}^k \mu_j x_j$

$x=\displaystyle\sum\limits_{1}^k\left ( \lambda_j- \alpha\mu_j \right )x_j$

选择 $\alpha$ 使得 $\alpha=min\left \{ \frac{\lambda_j}{\mu_j}, \mu_j\geq 0 \right \}=\frac{\lambda_j}{\mu _j},$ 对于某个 $i=1,2,...,k$

如果 $\mu_j\leq 0, \lambda_j-\alpha \mu_j\geq 0$

如果 $\mu_j> 0, then \:\frac{\lambda _j}{\mu_j}\geq \frac{\lambda_i}{\mu _i}=\alpha \Rightarrow \lambda_j-\alpha \mu_j\geq 0, j=1,2,...k$

特别是，$\lambda_i-\alpha \mu_i=0$，根据 $\alpha$ 的定义

$x=\displaystyle\sum\limits_{j=1}^k \left ( \lambda_j- \alpha\mu_j\right )x_j$,其中

$\lambda_j- \alpha\mu_j\geq0$ 且 $\displaystyle\sum\limits_{j=1}^k\left ( \lambda_j- \alpha\mu_j\right )=1$ 且 $\lambda_i- \alpha\mu_i=0$

因此，x 可以表示为最多 $k-1$ 个点的凸组合。

这个化简过程可以重复进行，直到 x 被表示为 $n+1$ 个元素的凸组合。

凸优化 - 魏尔斯特拉斯定理

设 S 为 $\mathbb{R}^n$ 中一个非空、闭合且有界的集合（也称为紧集），并设 $f:S\rightarrow \mathbb{R}$ 为 S 上的一个连续函数，则问题 min $\left \{ f\left ( x \right ):x \in S \right \}$ 取得其最小值。

证明

由于 S 非空且有界，因此存在下界。

$\alpha =Inf\left \{ f\left ( x \right ):x \in S \right \}$

现在设 $S_j=\left \{ x \in S:\alpha \leq f\left ( x \right ) \leq \alpha +\delta ^j\right \} \forall j=1,2,...$ 且 $\delta \in \left ( 0,1 \right )$

根据下确界的定义，对于每个 j，$S_j$ 都是非空的。

选择一些 $x_j \in S_j$ 以获得一个序列 $\left \{ x_j \right \}$，其中 j=1,2,...。

由于 S 有界，因此该序列也有界，并且存在一个收敛子序列 $\left \{ y_j \right \}$，它收敛于 $\hat{x}$。因此，$\hat{x}$ 是一个极限点，而 S 是闭合的，所以 $\hat{x} \in S$。由于 f 是连续的，所以 $f\left ( y_i \right )\rightarrow f\left ( \hat{x} \right )$。

由于 $\alpha \leq f\left ( y_i \right )\leq \alpha+\delta^k$，$\alpha=\displaystyle\lim_{k\rightarrow \infty}f\left ( y_i \right )=f\left ( \hat{x} \right )$

因此，$\hat{x}$ 是最小化解。

备注

魏尔斯特拉斯定理成立有两个重要的必要条件。如下所示 -

• **步骤 1** - 集合 S 应为有界集合。

  考虑函数 f\left $x \right$=x。

  它是一个无界集合，并且在它定义域的任何点都没有最小值。

  因此，为了获得最小值，S 应是有界的。

• **步骤 2** - 集合 S 应为闭合的。

  考虑函数 $f\left ( x \right )=\frac{1}{x}$，其定义域为 \left $0,1 \right$。

  此函数在给定定义域中不是闭合的，并且它的最小值也不存在。

  因此，为了获得最小值，S 应为闭合的。

凸优化 - 最近点定理

设 S 为 $\mathbb{R}^n$ 中一个非空闭凸集，并设 $y\notin S$，则存在一个点 $\bar{x}\in S$，其到 y 的距离最小，即 $\left \| y-\bar{x} \right \| \leq \left \| y-x \right \| \forall x \in S.$

此外，$\bar{x}$ 是一个最小化点当且仅当 $\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\leq 0$ 或 $\left ( y-\hat{x}, x-\hat{x} \right )\leq 0$

证明

最近点的存在性

由于 $S\ne \phi$，存在一个点 $\hat{x}\in S$，使得 S 到 y 的最小距离小于或等于 $\left \| y-\hat{x} \right \|。

定义 $\hat{S}=S \cap \left \{ x:\left \| y-x \right \|\leq \left \| y-\hat{x} \right \| \right \}$

由于 $\hat{S}$ 是闭合且有界的，并且由于范数是一个连续函数，因此根据魏尔斯特拉斯定理，存在一个最小点 $\hat{x} \in S$，使得 $\left \| y-\hat{x} \right \|=Inf\left \{ \left \| y-x \right \|,x \in S \right \}$

唯一性

假设 $\bar{x} \in S$，使得 $\left \| y-\hat{x} \right \|=\left \| y-\hat{x} \right \|= \alpha$

由于 S 是凸的，所以 $\frac{\hat{x}+\bar{x}}{2} \in S$

但是，$\left \| y-\frac{\hat{x}-\bar{x}}{2} \right \|\leq \frac{1}{2}\left \| y-\hat{x} \right \|+\frac{1}{2}\left \| y-\bar{x} \right \|=\alpha$

它不能是严格的不等式，因为 $\hat{x}$ 最接近 y。

因此，$\left \| y-\hat{x} \right \|=\mu \left \| y-\hat{x} \right \|，对于某些$\mu$

现在 $\left \| \mu \right \|=1.$ 如果 $\mu=-1$，则 $\left ( y-\hat{x} \right )=-\left ( y-\hat{x} \right )\Rightarrow y=\frac{\hat{x}+\bar{x}}{2} \in S$

但是 $y \in S$。因此矛盾。因此 $\mu=1 \Rightarrow \hat{x}=\bar{x}$

因此，最小化点是唯一的。

对于证明的第二部分，假设 $\left ( y-\hat{x} \right )^{\tau }\left ( x-\bar{x} \right )\leq 0$ 对于所有 $x\in S$

现在，

$\left \| y-x \right \|^{2}=\left \| y-\hat{x}+ \hat{x}-x\right \|^{2}=\left \| y-\hat{x} \right \|^{2}+\left \|\hat{x}-x \right \|^{2}+2\left (\hat{x}-x \right )^{\tau }\left ( y-\hat{x} \right )$

$\Rightarrow \left \| y-x \right \|^{2}\geq \left \| y-\hat{x} \right \|^{2}$ 因为 $\left \| \hat{x}-x \right \|^{2}\geq 0$ 且 $\left ( \hat{x}- x\right )^{T}\left ( y-\hat{x} \right )\geq 0$

因此，$\hat{x}$ 是最小化点。

反之，假设 $\hat{x}$ 是最小化点。

$\Rightarrow \left \| y-x \right \|^{2}\geq \left \| y-\hat{x} \right \|^2 \forall x \in S$

由于 S 是凸集。

$\Rightarrow \lambda x+\left ( 1-\lambda \right )\hat{x}=\hat{x}+\lambda\left ( x-\hat{x} \right ) \in S$ 对于 $x \in S$ 且 $\lambda \in \left ( 0,1 \right )$

现在，$\left \| y-\hat{x}-\lambda\left ( x-\hat{x} \right ) \right \|^{2}\geq \left \| y-\hat{x} \right \|^2$

并且

$\left \| y-\hat{x}-\lambda\left ( x-\hat{x} \right ) \right \|^{2}=\left \| y-\hat{x} \right \|^{2}+\lambda^2\left \| x-\hat{x} \right \|^{2}-2\lambda\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )$

$\Rightarrow \left \| y-\hat{x} \right \|^{2}+\lambda^{2}\left \| x-\hat{x} \right \|-2 \lambda\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\geq \left \| y-\hat{x} \right \|^{2}$

$\Rightarrow 2 \lambda\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\leq \lambda^2\left \| x-\hat{x} \right \|^2$

$\Rightarrow \left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\leq 0$

因此得证。

基本分离定理

设 S 为 $\mathbb{R}^n$ 中一个非空闭凸集，且 $y \notin S$。则存在一个非零向量 p 和标量 $\beta$，使得 $p^T y>\beta$ 且 $p^T x < \beta$ 对于每个 $x \in S$

证明

由于 S 是非空闭凸集，且 $y \notin S$，因此根据最近点定理，存在一个唯一的最小化点 $\hat{x} \in S$，使得

$\left ( x-\hat{x} \right )^T\left ( y-\hat{x} \right )\leq 0 \forall x \in S$

设 $p=\left ( y-\hat{x} \right )\neq 0$ 且 $\beta=\hat{x}^T\left ( y-\hat{x} \right )=p^T\hat{x}$。

则 $\left ( x-\hat{x} \right )^T\left ( y-\hat{x} \right )\leq 0$

$\Rightarrow \left ( y-\hat{x} \right )^T\left ( x-\hat{x} \right )\leq 0$

$\Rightarrow \left ( y-\hat{x} \right )^Tx\leq \left ( y-\hat{x} \right )^T \hat{x}=\hat{x}^T\left ( y-\hat{x} \right )$ 即，$p^Tx \leq \beta$

此外，$p^Ty-\beta=\left ( y-\hat{x} \right )^Ty-\hat{x}^T \left ( y-\hat{x} \right )$

$=\left ( y-\hat{x} \right )^T \left ( y-x \right )=\left \| y-\hat{x} \right \|^{2}>0$

$\Rightarrow p^Ty> \beta$

此定理导致分离超平面。基于上述定理的超平面可以定义如下 -

设 $S_1$ 和 $S_2$ 为 $\mathbb{R}$ 的非空子集，且 $H=\left \{ X:A^TX=b \right \}$ 为一个超平面。

• 如果 $A^TX \leq b \forall X \in S_1$ 且 $A_TX \geq b \forall X \in S_2$，则称超平面 H 分离 $S_1$ 和 $S_2$。

• 如果 $A^TX < b \forall X \in S_1$ 且 $A_TX > b \forall X \in S_2$，则称超平面 H 严格分离 $S_1$ 和 $S_2$。

• 如果 $A^TX \leq b \forall X \in S_1$ 且 $A_TX \geq b+ \varepsilon \forall X \in S_2$，其中 $\varepsilon$ 为一个正标量，则称超平面 H 强分离 $S_1$ 和 $S_2$。

凸优化 - 锥

如果 $x \in C\Rightarrow \lambda x \in C \forall \lambda \geq 0$，则称 $\mathbb{R}^n$ 中一个非空集合 C 为顶点为 0 的锥。

如果一个集合 C 既是凸的又是锥，则称其为凸锥。

例如，$y=\left | x \right |$ 不是凸锥，因为它不是凸的。

但是，$y \geq \left | x \right |$ 是一个凸锥，因为它既是凸的又是锥。

**注意** - 当且仅当对于任何 $x,y \in C$，$x+y \in C$ 时，锥 C 为凸的。

证明

由于 C 是锥，对于 $x,y \in C \Rightarrow \lambda x \in C$ 且 $\mu y \in C \:\forall \:\lambda, \mu \geq 0$

如果 $\lambda x + \left ( 1-\lambda \right )y \in C \: \forall \:\lambda \in \left ( 0, 1 \right )$，则 C 是凸的。

由于 C 是锥，$\lambda x \in C$ 且 $\left ( 1-\lambda \right )y \in C \Leftrightarrow x,y \in C$

因此，如果 $x+y \in C$，则 C 是凸的。

一般来说，如果 $x_1,x_2 \in C$，则 $\lambda_1x_1+\lambda_2x_2 \in C, \forall \lambda_1,\lambda_2 \geq 0$

示例

• $\mathbb{R}^n$ 中无限多个向量的锥组合是一个凸锥。

• 任何空集都是一个凸锥。

• 任何线性函数都是一个凸锥。

• 由于超平面是线性的，因此它也是一个凸锥。

• 闭半空间也是凸锥。

**注意** - 两个凸锥的交集是一个凸锥，但它们的并集可能是也可能不是凸锥。

凸优化 - 极锥

设 S 为 $\mathbb{R}^n$ 中一个非空集合，则 S 的极锥，记为 $S^*$，由 $S^*=\left \{p \in \mathbb{R}^n, p^Tx \leq 0 \: \forall x \in S \right \}$ 给出。

备注

• 即使 S 不是凸的，极锥也总是凸的。

• 如果 S 是空集，则 $S^*=\mathbb{R}^n$。

• 极性可以看作是正交性的推广。

设 $C\subseteq \mathbb{R}^n$，则 C 的正交空间，记为 $C^\perp =\left \{ y \in \mathbb{R}^n:\left \langle x,y \right \rangle=0 \forall x \in C \right \}$。

引理

设 $S,S_1$ 和 $S_2$ 为 $\mathbb{R}^n$ 中的非空集合，则以下陈述为真 -

• $S^*$ 是一个闭合凸锥。

• $S \subseteq S^{**}$，其中 $S^{**}$ 是 $S^*$ 的极锥。

• $S_1 \subseteq S_2 \Rightarrow S_{2}^{*} \subseteq S_{1}^{*}$。

证明

**步骤 1** - $S^*=\left \{ p \in \mathbb{R}^n,p^Tx\leq 0 \: \forall \:x \in S \right \}$

• 设 $x_1,x_2 \in S^*\Rightarrow x_{1}^{T}x\leq 0$ 且 $x_{2}^{T}x \leq 0,\forall x \in S$

  对于 $\lambda \in \left ( 0, 1 \right ),\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]^Tx=\left [ \left ( \lambda x_1 \right )^T+ \left \{\left ( 1-\lambda \right )x_{2} \right \}^{T}\right ]x, \forall x \in S$

  $=\left [ \lambda x_{1}^{T} +\left ( 1-\lambda \right )x_{2}^{T}\right ]x=\lambda x_{1}^{T}x+\left ( 1-\lambda \right )x_{2}^{T}\leq 0$

  因此 $\lambda x_1+\left ( 1-\lambda \right )x_{2} \in S^*$

  因此 $S^*$ 是一个凸集。

• 对于 $\lambda \geq 0,p^{T}x \leq 0, \forall \:x \in S$

  因此，$\lambda p^T x \leq 0,$

  $\Rightarrow \left ( \lambda p \right )^T x \leq 0$

  $\Rightarrow \lambda p \in S^*$

  因此，$S^*$ 是一个锥。

• 为了证明 $S^*$ 是闭合的，即要证明如果 $p_n \rightarrow p$ 当 $n \rightarrow \infty$ 时，则 $p \in S^*$

  $\forall x \in S, p_{n}^{T}x-p^T x=\left ( p_n-p \right )^T x$

  当 $p_n \rightarrow p$ 当 $n \rightarrow \infty \Rightarrow \left ( p_n \rightarrow p \right )\rightarrow 0$

  因此 $p_{n}^{T}x \rightarrow p^{T}x$。但是 $p_{n}^{T}x \leq 0, \: \forall x \in S$

  因此，$p^Tx \leq 0, \forall x \in S$

  $\Rightarrow p \in S^*$

  因此，$S^*$ 是闭合的。

**步骤 2** - $S^{**}=\left \{ q \in \mathbb{R}^n:q^T p \leq 0, \forall p \in S^*\right \}$

设 $x \in S$，则 $\forall p \in S^*, p^T x \leq 0 \Rightarrow x^Tp \leq 0 \Rightarrow x \in S^{**}$

因此，$S \subseteq S^{**}$

**步骤 3** - $S_2^*=\left \{ p \in \mathbb{R}^n:p^Tx\leq 0, \forall x \in S_2 \right \}$

由于 $S_1 \subseteq S_2 \Rightarrow \forall x \in S_2 \Rightarrow \forall x \in S_1$

因此，如果 $\hat{p} \in S_2^*,$则 $\hat{p}^Tx \leq 0,\forall x \in S_2$

$\Rightarrow \hat{p}^Tx\leq 0, \forall x \in S_1$

$\Rightarrow \hat{p}^T \in S_1^*$

$\Rightarrow S_2^* \subseteq S_1^*$

定理

设 C 为非空闭凸锥，则 $C=C^**$

证明

根据之前的引理，$C=C^{**}$。

要证明：$x \in C^{**} \subseteq C$

设 $x \in C^{**}$ 且 $x \notin C$

然后根据基本分离定理，存在一个非零向量 p 和一个标量 α，使得 $p^Ty \leq \alpha, \forall y \in C$

因此，$p^Tx > \alpha$

但由于 $\left ( y=0 \right ) \in C$ 且 $p^Ty\leq \alpha, \forall y \in C \Rightarrow \alpha\geq 0$ 且 $p^Tx>0$

如果 $p \notin C^*$，则存在某个 $\bar{y} \in C$ 使得 $p^T \bar{y}>0$，并且通过取足够大的 λ 可以使 $p^T\left ( \lambda \bar{y} \right )$ 任意大。

这与 $p^Ty \leq \alpha, \forall y \in C$ 的事实相矛盾。

因此，$p \in C^*$

由于 $x \in C^*=\left \{ q:q^Tp\leq 0, \forall p \in C^* \right \}$

因此，$x^Tp \leq 0 \Rightarrow p^Tx \leq 0$

但 $p^Tx> \alpha$

这是矛盾的。

因此，$x \in C$

因此 $C=C^{**}$。

凸优化 - 锥组合

形式为 $\alpha_1x_1+\alpha_2x_2+....+\alpha_nx_n$ 的点，其中 $\alpha_1, \alpha_2,...,\alpha_n\geq 0$，称为 $x_1, x_2,...,x_n$ 的锥组合。

• 如果 $x_i$ 在凸锥 C 中，则 $x_i$ 的每个锥组合也在 C 中。

• 如果一个集合 C 包含其所有元素的锥组合，则 C 是一个凸锥。

锥包

锥包定义为给定集合 S 的所有锥组合的集合，记为 coni$S$。

因此，$coni\left ( S \right )=\left \{ \displaystyle\sum\limits_{i=1}^k \lambda_ix_i:x_i \in S,\lambda_i\in \mathbb{R}, \lambda_i\geq 0,i=1,2,...\right \}$

• 锥包是凸集。
• 原点始终属于锥包。

凸优化 - 多面体集

如果 $\mathbb{R}^n$ 中的一个集合是有限个闭半空间的交集，则称该集合为多面体集，即

$S=\left \{ x \in \mathbb{R}^n:p_{i}^{T}x\leq \alpha_i, i=1,2,....,n \right \}$

例如，

• $\left \{ x \in \mathbb{R}^n:AX=b \right \}$

• $\left \{ x \in \mathbb{R}^n:AX\leq b \right \}$

• $\left \{ x \in \mathbb{R}^n:AX\geq b \right \}$

多面体锥

如果 $\mathbb{R}^n$ 中的一个集合是有限个包含原点的半空间的交集，则称该集合为多面体锥，即 $S=\left \{ x \in \mathbb{R}^n:p_{i}^{T}x\leq 0, i=1, 2,... \right \}$

多胞体

多胞体是有界的多面体集。

备注

• 多胞体是有限个点的凸包。
• 多面体锥是由有限个向量生成的。
• 多面体集是闭集。
• 多面体集是凸集。

凸集的极点

设 S 是 $\mathbb{R}^n$ 中的凸集。如果 $x \in S$ 且 $x= \lambda x_1+\left ( 1-\lambda \right )x_2$，其中 $x_1, x_2 \in S$ 且 $\lambda \in\left ( 0, 1 \right )$ 蕴含 $x=x_1=x_2$，则称 $x$ 为 S 的极点。

示例

步骤 1 − $S=\left \{ \left ( x_1,x_2 \right ) \in \mathbb{R}^2:x_{1}^{2}+x_{2}^{2}\leq 1 \right \}$

极点，$E=\left \{ \left ( x_1, x_2 \right )\in \mathbb{R}^2:x_{1}^{2}+x_{2}^{2}= 1 \right \}$

步骤 2 − $S=\left \{ \left ( x_1,x_2 \right )\in \mathbb{R}^2:x_1+x_2< 2, -x_1+2x_2\leq 2, x_1,x_2\geq 0 \right \}$

极点，$E=\left \{ \left ( 0, 0 \right), \left ( 2, 0 \right), \left ( 0, 1 \right), \left ( \frac{2}{3}, \frac{4}{3} \right) \right \}$

步骤 3 − S 是由点 $\left \{ \left ( 0,0 \right ), \left ( 1,1 \right ), \left ( 1,3 \right ), \left ( -2,4 \right ),\left ( 0,2 \right ) \right \}$ 组成的多胞体。

极点，$E=\left \{ \left ( 0,0 \right ), \left ( 1,1 \right ),\left ( 1,3 \right ),\left ( -2,4 \right ) \right \}$

备注

• 凸集 S 的任何点都可以表示为其极点的凸组合。

• 这仅适用于 $\mathbb{R}^n$ 中的闭有界集。

• 对于无界集，这可能不成立。

k 个极点

凸集中的一个点称为 k 个极点当且仅当它是 S 内 k 维凸集的内点，并且它不是 S 内 $k+1$ 维凸集的内点。基本上，对于凸集 S，k 个极点构成 k 维开面。

凸优化 - 方向

设 S 是 $\mathbb{R}^n$ 中的闭凸集。如果对于每个 $x \in S$，$x+\lambda d \in S, \forall \lambda \geq 0$，则非零向量 $d \in \mathbb{R}^n$ 称为 S 的方向。

• 如果对于 $\alpha>0$，$d \neq \alpha d_2$，则 S 的两个方向 $d_1$ 和 $d_2$ 称为不同的方向。

• 如果方向 d 不能写成两个不同方向的正线性组合，即如果 $d=\lambda _1d_1+\lambda _2d_2$，其中 $\lambda _1, \lambda _2>0$，则 $d_1= \alpha d_2$，其中 α 为某个数，则称 S 的方向 d 为极方向。

• 任何其他方向都可以表示为极方向的正组合。

• 对于凸集 $S$，如果对于某个 $x \in S$ 和所有 $\lambda \geq0$，$x+\lambda d \in S$，则方向 d 称为 $S$ 的**隐退方向**。

• 设 E 是某个函数 $f:S \rightarrow$ 在 $\mathbb{R}^n$ 中的非空凸集 S 上取得最大值的点的集合，则 E 称为 S 的暴露面。暴露面的方向称为暴露方向。

• 方向为极方向的射线称为极射线。

示例

考虑函数 $f\left ( x \right )=y=\left |x \right |$，其中 $x \in \mathbb{R}^n$。设 d 是 $\mathbb{R}^n$ 中的单位向量。

则 d 是函数 f 的方向，因为对于任何 $\lambda \geq 0$，$x+\lambda d \in f\left ( x \right )$。

凸函数和凹函数

设 $f:S \rightarrow \mathbb{R}$，其中 S 是 $\mathbb{R}^n$ 中的非空凸集，则如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0,1 \right )$，则称 $f\left ( x \right )$ 在 S 上是凸的。

另一方面，设 $f:S\rightarrow \mathbb{R}$，其中 S 是 $\mathbb{R}^n$ 中的非空凸集，则如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\geq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$，则称 $f\left ( x \right )$ 在 S 上是凹的。

设 $f:S \rightarrow \mathbb{R}$，其中 S 是 $\mathbb{R}^n$ 中的非空凸集，则如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$，则称 $f\left ( x\right )$ 在 S 上是严格凸的。

设 $f:S \rightarrow \mathbb{R}$，其中 S 是 $\mathbb{R}^n$ 中的非空凸集，则如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )> \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$，则称 $f\left ( x\right )$ 在 S 上是严格凹的。

示例

• 线性函数既是凸函数又是凹函数。

• $f\left ( x \right )=\left | x \right |$ 是凸函数。

• $f\left ( x \right )= \frac{1}{x}$ 是凸函数。

定理

设 $f_1,f_2,...,f_k:\mathbb{R}^n \rightarrow \mathbb{R}$ 是凸函数。考虑函数 $f\left ( x \right )=\displaystyle\sum\limits_{j=1}^k \alpha_jf_j\left ( x \right )$，其中 $\alpha_j>0,j=1, 2, ...k,$ 则 $f\left ( x \right )$ 是凸函数。

证明

由于 $f_1,f_2,...f_k$ 是凸函数

因此，$f_i\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f_i\left ( x_1 \right )+\left ( 1-\lambda \right )f_i\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$ 且 $i=1, 2,....,k$

考虑函数 $f\left ( x \right )$。

因此，

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )$

$=\displaystyle\sum\limits_{j=1}^k \alpha_jf_j\left ( \lambda x_1 +1-\lambda \right )x_2\leq \displaystyle\sum\limits_{j=1}^k\alpha_j\lambda f_j\left ( x_1 \right )+\left ( 1-\lambda \right )f_j\left ( x_2 \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda \left ( \displaystyle\sum\limits_{j=1}^k \alpha _jf_j\left ( x_1 \right ) \right )+\left ( \displaystyle\sum\limits_{j=1}^k \alpha _jf_j\left ( x_2 \right ) \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_2 \right )\leq \left ( 1-\lambda \right )f\left ( x_2 \right )$

因此，$f\left ( x\right )$ 是凸函数。

定理

设 $f\left ( x\right )$ 是凸集 $S\subset \mathbb{R}^n$ 上的凸函数，则 $f\left ( x\right )$ 在 S 上的局部最小值是全局最小值。

证明

设 $\hat{x}$ 是 $f\left ( x \right )$ 的局部最小值，且 $\hat{x}$ 不是全局最小值。

因此，存在 $\hat{x} \in S$ 使得 $f\left ( \bar{x} \right )< f\left ( \hat{x} \right )$

由于 $\hat{x}$ 是局部最小值，因此存在邻域 $N_\varepsilon \left ( \hat{x} \right )$ 使得 $f\left ( \hat{x} \right )\leq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \hat{x} \right )\cap S$

但 $f\left ( x \right )$ 是 S 上的凸函数，因此对于 $\lambda \in \left ( 0, 1 \right )$

我们有 $\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}\leq \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left ( \bar{x} \right )$

$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left (\hat{x} \right )$

$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< f\left (\hat{x} \right ), \forall \lambda \in \left ( 0,1 \right )$

但对于某个 $\lambda<1$ 但接近 1 的值，我们有

$\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \in N_\varepsilon \left ( \hat{x} \right )\cap S$ 且 $f\left ( \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \right )< f\left ( \bar{x} \right )$

这是矛盾的。

因此，$\bar{x}$ 是全局最小值。

上图

设 S 是 $\mathbb{R}^n$ 中的非空子集，设 $f:S \rightarrow \mathbb{R}$，则 f 的上图记为 epi$f$ 或 $E_f$，它是 $\mathbb{R}^n+1$ 的一个子集，定义为 $E_f=\left \{ \left ( x,\alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\leq \alpha \right \}$

下图

设 S 是 $\mathbb{R}^n$ 中的非空子集，设 $f:S \rightarrow \mathbb{R}$，则 f 的下图记为 hyp$f$ 或 $H_f=\left \{ \left ( x, \alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\geq \alpha \right \}$

定理

设 S 是 $\mathbb{R}^n$ 中的非空凸集，设 $f:S \rightarrow \mathbb{R}^n$，则 f 是凸的当且仅当其上图 $E_f$ 是凸集。

证明

设 f 是凸函数。

要证明 $E_f$ 是凸集。

设 $\left ( x_1, \alpha_1 \right ),\left ( x_2, \alpha_2 \right ) \in E_f,\lambda \in\left ( 0, 1 \right )$

要证明 $\lambda \left ( x_1,\alpha_1 \right )+\left ( 1-\lambda \right )\left ( x_2, \alpha_2 \right ) \in E_f$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2 \right ]\in E_f$

$f\left ( x_1 \right )\leq \alpha _1, f\left ( x_2\right )\leq \alpha _2$

因此，$f\left (\lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f \left ( x_2 \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2$

逆命题

假设 $E_f$ 是一个凸集。

要证明 f 是凸函数。

即，要证明如果 $x_1, x_2 \in S,\lambda \left ( 0, 1\right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

假设 $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right ),f\left ( x_1 \right ), f\left ( x_2 \right ) \in \mathbb{R}$

由于 $E_f$ 是一个凸集，$\left ( \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )\right )f\left ( x_2 \right )\in E_f$

因此，$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

凸优化 - Jensen 不等式

假设 S 是 $\mathbb{R}^n$ 中的一个非空凸集，且 $f:S \rightarrow \mathbb{R}^n$。则 f 是凸函数当且仅当对于每个整数 $k>0$

$x_1,x_2,...x_k \in S, \displaystyle\sum\limits_{i=1}^k \lambda_i=1, \lambda_i\geq 0, \forall i=1,2,s,k$，有 $f\left ( \displaystyle\sum\limits_{i=1}^k \lambda_ix_i \right )\leq \displaystyle\sum\limits_{i=1}^k \lambda _if\left ( x \right )$

证明

通过数学归纳法证明。

$k=1:x_1 \in S$ 因此 $f\left ( \lambda_1 x_1\right ) \leq \lambda_i f\left (x_1\right )$，因为 $\lambda_i=1$。

$k=2:\lambda_1+\lambda_2=1$ 且 $x_1, x_2 \in S$

因此，$\lambda_1x_1+\lambda_2x_2 \in S$

因此根据定义，$f\left ( \lambda_1 x_1 +\lambda_2 x_2 \right )\leq \lambda _1f\left ( x_1 \right )+\lambda _2f\left ( x_2 \right )$

假设该命题对于 $n < k$ 成立

因此，

$f\left ( \lambda_1 x_1+ \lambda_2 x_2+....+\lambda_k x_k\right )\leq \lambda_1 f\left (x_1 \right )+\lambda_2 f\left (x_2 \right )+...+\lambda_k f\left (x_k \right )$

$k=n+1:$ 假设 $x_1, x_2,....x_n,x_{n+1} \in S$ 且 $\displaystyle\sum\limits_{i=1}^{n+1}=1$

因此 $\mu_1x_1+\mu_2x_2+.......+\mu_nx_n+\mu_{n+1} x_{n+1} \in S$

因此，$f\left (\mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1} x_{n+1} \right )$

$=f\left ( \left ( \mu_1+\mu_2+...+\mu_n \right)\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+\mu_3}+\mu_{n+1}x_{n+1} \right)$

$=f\left ( \mu_y+\mu_{n+1}x_{n+1} \right )$ 其中 $\mu=\mu_1+\mu_2+...+\mu_n$ 且

$y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n}$ 并且 $\mu_1+\mu_{n+1}=1,y \in S$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq \mu f\left ( y \right )+\mu_{n+1} f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq$

$\left ( \mu_1+\mu_2+...+\mu_n \right )f\left ( \frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n} \right )+\mu_{n+1}f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n +\mu_{n+1}x_{n+1}\right )\leq \left ( \mu_1+ \mu_2+ ...+\mu_n \right )$

$\left [ \frac{\mu_1}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_1 \right )+...+\frac{\mu_n}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_n \right ) \right ]+\mu_{n+1}f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right )\leq \mu_1f\left ( x_1 \right )+\mu_2f\left ( x_2 \right )+....$

因此得证。

凸优化 - 可微函数

假设 S 是 $\mathbb{R}^n$ 中的一个非空开集，则 $f:S\rightarrow \mathbb{R}$ 在 $\hat{x} \in S$ 处可微，如果存在一个向量 $\bigtriangledown f\left ( \hat{x} \right )$（称为梯度向量）和一个函数 $\alpha :\mathbb{R}^n\rightarrow \mathbb{R}$，使得

$f\left ( x \right )=f\left ( \hat{x} \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x-\hat{x} \right )+\left \| x=\hat{x} \right \|\alpha \left ( \hat{x}, x-\hat{x} \right ), \forall x \in S$ 其中

$\alpha \left (\hat{x}, x-\hat{x} \right )\rightarrow 0 \bigtriangledown f\left ( \hat{x} \right )=\left [ \frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_2}...\frac{\partial f}{\partial x_n} \right ]_{x=\hat{x}}^{T}$

定理

假设 S 是 $\mathbb{R}^n$ 中的一个非空、开凸集，且 $f:S\rightarrow \mathbb{R}$ 在 S 上可微。则 f 是凸函数当且仅当对于 $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f\left ( x_2 \right )$

证明

假设 f 是一个凸函数。即，对于 $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right )$

$f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

$\Rightarrow f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )+f\left ( x_2 \right )$

$\Rightarrow\lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2+\lambda \left ( x_1-x_2 \right ) \right )-f\left ( x_2 \right )$

$\Rightarrow \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\lambda +$

$\left \| \lambda \left ( x_1-x_2 \right ) \right \|\alpha \left ( x_2,\lambda\left (x_1 - x_2 \right )-f\left ( x_2 \right ) \right )$

其中 $\alpha\left ( x_2, \lambda\left (x_1 - x_2 \right ) \right )\rightarrow 0$ 当 $\lambda \rightarrow 0$

两边除以 $\lambda$，得到：

$f\left ( x_1 \right )-f\left ( x_2 \right ) \geq \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right )$

逆命题

假设对于 $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f \left ( x_2 \right )$

要证明 f 是凸函数。

由于 S 是凸集，$x_3=\lambda x_1+\left (1-\lambda \right )x_2 \in S, \lambda \in \left ( 0, 1 \right )$

由于 $x_1, x_3 \in S$，因此

$f\left ( x_1 \right )-f \left ( x_3 \right ) \geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 -x_3\right )$

$\Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - \lambda x_1-\left (1-\lambda \right )x_2\right )$

$\Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \left ( 1- \lambda\right )\bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - x_2\right )$

由于 $x_2, x_3 \in S$，因此

$f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )$

$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-\lambda x_1-\left ( 1-\lambda \right )x_2 \right )$

$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \left ( -\lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )$

因此，结合上述等式，得到：

$\lambda \left ( f\left ( x_1 \right )-f\left ( x_3 \right ) \right )+\left ( 1- \lambda \right )\left ( f\left ( x_2 \right )-f\left ( x_3 \right ) \right )\geq 0$

$\Rightarrow f\left ( x_3\right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

定理

假设 S 是 $\mathbb{R}^n$ 中的一个非空开凸集，且 $f:S \rightarrow \mathbb{R}$ 在 S 上可微，则 f 在 S 上是凸函数当且仅当对于任意 $x_1,x_2 \in S,\left ( \bigtriangledown f \left ( x_2 \right )-\bigtriangledown f \left ( x_1 \right ) \right )^T \left ( x_2-x_1 \right ) \geq 0$

证明

假设 f 是一个凸函数，则利用之前的定理：

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\leq f\left ( x_1 \right )-f\left ( x_2 \right )$ 且

$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$

将上述两个等式相加，得到：

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_2-x_1 \right )\geq 0$

逆命题

假设对于任意 $x_1,x_2 \in S,\left (\bigtriangledown f \left ( x_2\right )- \bigtriangledown f \left ( x_1\right )\right )^T \left ( x_2-x_1\right )\geq 0$

要证明 f 是凸函数。

假设 $x_1,x_2 \in S$，则根据中值定理，$\frac{f\left ( x_1\right )-f\left ( x_2\right )}{x_1-x_2}=\bigtriangledown f\left ( x\right ),x \in \left ( x_1-x_2\right ) \Rightarrow x= \lambda x_1+\left ( 1-\lambda\right )x_2$，因为 S 是一个凸集。

$\Rightarrow f\left ( x_1 \right )- f\left ( x_2 \right )=\left ( \bigtriangledown f\left ( x \right )^T \right )\left ( x_1-x_2 \right )$

对于 $x,x_1$，我们知道：

$\left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x-x_1 \right )\geq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( \lambda x_1+\left ( 1-\lambda \right )x_2-x_1 \right )\geq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x \right )- \bigtriangledown f\left ( x_1 \right )\right )^T\left ( 1- \lambda \right )\left ( x_2-x_1 \right )\geq 0$

$\Rightarrow \bigtriangledown f\left ( x \right )^T\left ( x_2-x_1 \right )\geq \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )$

结合上述等式，得到：

$\Rightarrow \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$

因此，利用最后一个定理，f 是一个凸函数。

二阶可微函数

假设 S 是 $\mathbb{R}^n$ 的一个非空子集，且 $f:S\rightarrow \mathbb{R}$，则 f 在 $\bar{x} \in S$ 处二阶可微，如果存在一个向量 $\bigtriangledown f\left (\bar{x}\right )$、一个 $n \times n$ 矩阵 $H\left (x\right )$$称为Hessian矩阵$ 和一个函数 $\alpha:\mathbb{R}^n \rightarrow \mathbb{R}$，使得 $f\left ( x \right )=f\left ( \bar{x}+x-\bar{x} \right )=f\left ( \bar{x} \right )+\bigtriangledown f\left ( \bar{x} \right )^T\left ( x-\bar{x} \right )+\frac{1}{2}\left ( x-\bar{x} \right )H\left ( \bar{x} \right )\left ( x-\bar{x} \right )$

其中 $\alpha \left ( \bar{x}, x-\bar{x} \right )\rightarrow Oasx\rightarrow \bar{x}$

全局最优的充分必要条件

定理

设 f 是一个二阶可微函数。如果 $\bar{x}$ 是一个局部最小值点，则 $\bigtriangledown f\left ( \bar{x} \right )=0$ 且 Hessian 矩阵 $H\left ( \bar{x} \right )$ 是半正定的。

证明

设 $d \in \mathbb{R}^n$。由于 f 在 $\bar{x}$ 处二阶可微。

因此，

$f\left ( \bar{x} +\lambda d\right )=f\left ( \bar{x} \right )+\lambda \bigtriangledown f\left ( \bar{x} \right )^T d+\lambda^2d^TH\left ( \bar{x} \right )d+\lambda^2d^TH\left ( \bar{x} \right )d+$

$\lambda^2\left \| d \right \|^2\beta \left ( \bar{x}, \lambda d \right )$

但 $\bigtriangledown f\left ( \bar{x} \right )=0$ 且 $\beta\left ( \bar{x}, \lambda d \right )\rightarrow 0$ 当 $\lambda \rightarrow 0$

$\Rightarrow f\left ( \bar{x} +\lambda d \right )-f\left ( \bar{x} \right )=\lambda ^2d^TH\left ( \bar{x} \right )d$

由于 $\bar{x }$ 是一个局部最小值点，存在一个 $\delta > 0$ 使得 $f\left ( x \right )\leq f\left ( \bar{x}+\lambda d \right ), \forall \lambda \in \left ( 0,\delta \right )$

定理

设 $f:S \rightarrow \mathbb{R}^n$，其中 $S \subset \mathbb{R}^n$ 在 S 上二阶可微。如果 $\bigtriangledown f\left ( x\right )=0$ 且 $H\left ( \bar{x} \right )$ 对所有 $x \in S$ 都是半正定的，则 $\bar{x}$ 是一个全局最优解。

证明

由于 $H\left ( \bar{x} \right )$ 是半正定的，f 是 S 上的凸函数。由于 f 在 $\bar{x}$ 处可微且凸

$\bigtriangledown f\left ( \bar{x} \right )^T \left ( x-\bar{x} \right ) \leq f\left (x\right )-f\left (\bar{x}\right ),\forall x \in S$

由于 $\bigtriangledown f\left ( \bar{x} \right )=0, f\left ( x \right )\geq f\left ( \bar{x} \right )$

因此，$\bar{x}$ 是一个全局最优解。

定理

假设 $\bar{x} \in S$ 是问题 $f:S \rightarrow \mathbb{R}$ 的局部最优解，其中 S 是 $\mathbb{R}^n$ 的非空子集，且 S 是凸的。$min \:f\left ( x \right )$，其中 $x \in S$。

则

• $\bar{x}$ 是一个全局最优解。

• 如果 $\bar{x}$ 是严格局部最小值点或 f 是严格凸函数，则 $\bar{x}$ 是唯一的全局最优解，也是严格局部最小值点。

证明

设 $\bar{x}$ 是问题的另一个全局最优解，使得 $x \neq \bar{x}$ 且 $f\left ( \bar{x} \right )=f\left ( \hat{x} \right )$

由于 $\hat{x},\bar{x} \in S$ 且 S 是凸的，则 $\frac{\hat{x}+\bar{x}}{2} \in S$ 且 f 是严格凸的。

$\Rightarrow f\left ( \frac{\hat{x}+\bar{x}}{2} \right )< \frac{1}{2} f\left (\bar{x}\right )+\frac{1}{2} f\left (\hat{x}\right )=f\left (\hat{x}\right )$

这是矛盾的。

因此，$\hat{x}$ 是唯一的全局最优解。

推论

设 $f:S \subset \mathbb{R}^n \rightarrow \mathbb{R}$ 是一个可微凸函数，其中 $\phi \neq S\subset \mathbb{R}^n$ 是一个凸集。考虑问题 $min f\left (x\right ),x \in S$，则 $\bar{x}$ 是一个最优解，当且仅当 $\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right ) \geq 0,\forall x \in S.$

证明

设 $\bar{x}$ 是一个最优解，即 $f\left (\bar{x}\right )\leq f\left (x\right ),\forall x \in S$

$\Rightarrow f\left (x\right )=f\left (\bar{x}\right )\geq 0$

$f\left (x\right )=f\left (\bar{x}\right )+\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )+\left \| x-\bar{x} \right \|\alpha \left ( \bar{x},x-\bar{x} \right )$

其中 $\alpha \left ( \bar{x},x-\bar{x} \right )\rightarrow 0$ 当 $x \rightarrow \bar{x}$

$\Rightarrow f\left (x\right )-f\left (\bar{x}\right )=\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )\geq 0$

推论

设 f 是一个在 $\bar{x}$ 处可微的凸函数，则 $\bar{x}$ 是全局最小值点当且仅当 $\bigtriangledown f\left (\bar{x}\right )=0$

示例

• $f\left (x\right )=\left (x^2-1\right )^{3}, x \in \mathbb{R}$。

  $\bigtriangledown f\left (x\right )=0 \Rightarrow x= -1,0,1$。

  $\bigtriangledown^2f\left (\pm 1 \right )=0, \bigtriangledown^2 f\left (0 \right )=6>0$。

  $f\left (\pm 1 \right )=0,f\left (0 \right )=-1$

  因此，$f\left (x \right ) \geq -1=f\left (0 \right )\Rightarrow f\left (0 \right ) \leq f \left (x \right)\forall x \in \mathbb{R}$

• $f\left (x \right )=x\log x$ 定义在 $S=\left \{ x \in \mathbb{R}, x> 0 \right \}$ 上。

  ${f}'x=1+\log x$

  ${f}''x=\frac{1}{x}>0$

  因此，此函数是严格凸的。

• $f \left (x \right )=e^{x},x \in \mathbb{R}$ 是严格凸的。

拟凸函数和拟凹函数

设 $f:S \rightarrow \mathbb{R}$，其中 $S \subset \mathbb{R}^n$ 是一个非空凸集。如果对于每个 $x_1,x_2 \in S$，都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\lambda \in \left ( 0, 1 \right )$，则称函数 f 为拟凸函数。

例如，$f\left ( x \right )=x^{3}$

设 $f:S\rightarrow R$，其中 $S\subset \mathbb{R}^n$ 是一个非空凸集。如果对于每个 $x_1, x_2 \in S$，都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\geq min\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}, \lambda \in \left ( 0, 1 \right )$，则称函数 f 为拟凹函数。

备注

• 每个凸函数都是拟凸函数，但反之不成立。
• 既是拟凸函数又是拟凹函数的函数称为拟单调函数。

定理

设 $f:S\rightarrow \mathbb{R}$ 且 S 是 $\mathbb{R}^n$ 中的非空凸集。函数 f 是拟凸函数当且仅当 $S_{\alpha} =\left ( x \in S:f\left ( x \right )\leq \alpha \right \}$ 对每个实数 \alpha 都是凸的。

证明

设 f 在 S 上是拟凸的。

设 $x_1,x_2 \in S_{\alpha}$，因此 $x_1,x_2 \in S$ 且 $max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\leq \alpha$

设 $\lambda \in \left (0, 1 \right )$ 且设 $x=\lambda x_1+\left ( 1-\lambda \right )x_2\leq max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\Rightarrow x \in S$

因此，$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}\leq \alpha$

因此，$S_{\alpha}$ 是凸的。

逆命题

设 $S_{\alpha}$ 对每个 $\alpha$ 都是凸的

$x_1,x_2 \in S, \lambda \in \left ( 0,1\right )$

$x=\lambda x_1+\left ( 1-\lambda \right )x_2$

设 $x=\lambda x_1+\left ( 1-\lambda \right )x_2$

对于 $x_1, x_2 \in S_{\alpha}, \alpha= max \left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}$

$\Rightarrow \lambda x_1+\left (1-\lambda \right )x_2 \in S_{\alpha}$

$\Rightarrow f \left (\lambda x_1+\left (1-\lambda \right )x_2 \right )\leq \alpha$

因此得证。

定理

设 $f:S\rightarrow \mathbb{R}$ 且 S 是 $\mathbb{R}^n$ 中的非空凸集。函数 f 是拟凹函数当且仅当 $S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ 对每个实数 $\alpha$ 都是凸的。

定理

设 $f:S\rightarrow \mathbb{R}$ 且 S 是 $\mathbb{R}^n$ 中的非空凸集。函数 f 是拟单调函数当且仅当 $S_{\alpha} =\left \{ x \in S:f\left ( x \right )= \alpha \right \}$ 对每个实数 $\alpha$ 都是凸的。

可微拟凸函数

定理

设 S 是 $\mathbb{R}^n$ 中的非空凸集，且 $f:S \rightarrow \mathbb{R}$ 在 S 上可微，则 f 是拟凸函数当且仅当对于任意 $x_1,x_2 \in S$ 且 $f\left ( x_1 \right )\leq f\left ( x_2 \right )$，都有 $\bigtriangledown f\left ( x_2 \right )^T\left ( x_2-x_1 \right )\leq 0$

证明

设 f 是一个拟凸函数。

设 $x_1,x_2 \in S$ 使得 $f\left ( x_1 \right ) \leq f\left ( x_2 \right )$

根据 f 在 $x_2$ 处的可微性，$\lambda \in \left ( 0, 1 \right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=f\left ( x_2+\lambda \left (x_1-x_2 \right ) \right )=f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1-x_2 \right ) \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )-f\left ( x_2 \right )-f\left ( x_2 \right )=\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x2, \lambda\left ( x_1-x_2 \right )\right )$

但由于 f 是拟凸的，$f \left ( \lambda x_1+ \left ( 1- \lambda \right )x_2 \right )\leq f \left (x_2 \right )$

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right ) \right )\leq 0$

但 $\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right )\right )\rightarrow 0$ 当 $\lambda \rightarrow 0$

因此，$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right ) \leq 0$

逆命题

设对于 $x_1,x_2 \in S$ 且 $f\left ( x_1 \right )\leq f\left ( x_2 \right )$，$\bigtriangledown f\left ( x_2 \right )^T \left ( x_1,x_2 \right ) \leq 0$

要证明 f 是拟凸的，即 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq f\left ( x_2 \right )$

反证法

假设存在一个 $x_3= \lambda x_1+\left ( 1-\lambda \right )x_2$ 使得 $f\left ( x_2 \right )< f \left ( x_3 \right )$ 对于某些 $\lambda \in \left ( 0, 1 \right )$

对于 $x_2$ 和 $x_3$，$\bigtriangledown f\left ( x_3 \right )^T \left ( x_2-x_3 \right ) \leq 0$

$\Rightarrow -\lambda \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\geq 0$

对于 $x_1$ 和 $x_3$，$\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_3 \right ) \leq 0$

$\Rightarrow \left ( 1- \lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\leq 0$

因此，根据上述等式，$\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )=0$

定义 $U=\left \{ x:f\left ( x \right )\leq f\left ( x_2 \right ),x=\mu x_2+\left ( 1-\mu \right )x_3, \mu \in \left ( 0,1 \right ) \right \}$

因此，我们可以找到 $x_0 \in U$ 使得 $x_0 = \mu_0 x_2= \mu x_2+\left ( 1- \mu \right )x_3$ 对于某些 $\mu _0 \in \left ( 0,1 \right )$，它最接近 $x_3$，并且 $\hat{x} \in \left ( x_0,x_1 \right )$ 使得根据中值定理，

$$\frac{f\left ( x_3\right )-f\left ( x_0\right )}{x_3-x_0}= \bigtriangledown f\left ( \hat{x}\right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x_3-x_0 \right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\mu_0 \lambda f\left ( \hat{x}\right )^T \left ( x_1-x_2 \right )$$

由于 $x_0$ 是 $x_1$ 和 $x_2$ 的组合，并且 $f\left (x_2 \right )< f\left ( \hat{x}\right )$

通过重复起始过程，$\bigtriangledown f \left ( \hat{x}\right )^T \left ( x_1-x_2\right )=0$

因此，结合上述等式，我们得到

$$f\left ( x_3\right )=f\left ( x_0 \right ) \leq f\left ( x_2\right )$$

$$\Rightarrow f\left ( x_3\right )\leq f\left ( x_2\right )$$

因此，这是一个矛盾。

示例

步骤 1 − $f\left ( x\right )=X^3$

$设 f \left ( x_1\right )\leq f\left ( x_2\right )$

$\Rightarrow x_{1}^{3}\leq x_{2}^{3}\Rightarrow x_1\leq x_2$

$\bigtriangledown f\left ( x_2 \right )\left ( x_1-x_2 \right )=3x_{2}^{2}\left ( x_1-x_2 \right )\leq 0$

因此，$f\left ( x\right )$ 是拟凸的。

步骤 2 − $f\left ( x\right )=x_{1}^{3}+x_{2}^{3}$

设 $\hat{x_1}=\left ( 2, -2\right )$ 和 $\hat{x_2}=\left ( 1, 0\right )$

因此，$f\left ( \hat{x_1}\right )=0,f\left ( \hat{x_2}\right )=1 \Rightarrow f\left ( \hat{x_1}\right )\setminus < f \left ( \hat{x_2}\right )$

因此，$\bigtriangledown f \left ( \hat{x_2}\right )^T \left ( \hat{x_1}- \hat{x_2}\right )= \left ( 3, 0\right )^T \left ( 1, -2\right )=3 >0$

因此 $f\left ( x\right )$ 不是拟凸的。

严格拟凸函数

设 $f:S\rightarrow \mathbb{R}^n$，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集，则如果对于每个 $x_1,x_2 \in S$ 且 $f\left ( x_1 \right ) \neq f\left ( x_2 \right )$，都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}$，则称 f 为严格拟凸函数。

备注

• 每个严格拟凸函数都是严格凸函数。
• 严格拟凸函数不蕴含拟凸性。
• 严格拟凸函数可能不是强拟凸函数。
• 伪凸函数是严格拟凸函数。

定理

设 $f:S\rightarrow \mathbb{R}^n$ 是严格拟凸函数，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集。考虑问题：$min \:f\left ( x \right ), x \in S$。如果 $\hat{x}$ 是局部最优解，则 $\bar{x}$ 是全局最优解。

证明

假设存在 $\bar{x} \in S$ 使得 $f\left ( \bar{x}\right )\leq f \left ( \hat{x}\right )$。

由于 $\bar{x},\hat{x} \in S$ 且 S 是凸集，因此，

$$\lambda \bar{x}+\left ( 1-\lambda \right )\hat{x}\in S, \forall \lambda \in \left ( 0,1 \right )$$

由于 $\hat{x}$ 是局部最小值，所以 $f\left ( \hat{x} \right ) \leq f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right ), \forall \lambda \in \left ( 0,\delta \right )$。

由于 f 是严格拟凸函数。

$$f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right )< max \left \{ f\left ( \hat{x} \right ),f\left ( \bar{x} \right ) \right \}=f\left ( \hat{x} \right )$$

因此，这是一个矛盾。

严格拟凹函数

设 $f:S\rightarrow \mathbb{R}^n$，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集，则如果对于每个 $x_1,x_2 \in S$ 且 $f\left (x_1\right )\neq f\left (x_2\right )$，都有

$$f\left (\lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$$ .

示例

• $f\left (x\right )=x^2-2$

  这是一个严格拟凸函数，因为如果我们在满足定义中约束条件的域中取任意两点 $x_1,x_2$，则有 $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )< max \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$。因为该函数在负 x 轴上递减，在正 x 轴上递增（因为它是抛物线）。

• $f\left (x\right )=-x^2$

  这不是一个严格拟凸函数，因为如果我们取 $x_1=1$ 和 $x_2=-1$ 以及 $\lambda=0.5$，则 $f\left (x_1\right )=-1=f\left (x_2\right )$，但 $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )=0$。因此它不满足定义中陈述的条件。但它是一个拟凹函数，因为如果我们在满足定义中约束条件的域中取任意两点，则有 $f\left ( \lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$。因为该函数在负 x 轴上递增，在正 x 轴上递减。

强拟凸函数

设 $f:S\rightarrow \mathbb{R}^n$，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集，则如果对于任何 $x_1,x_2 \in S$ 且 $\left ( x_1 \right ) \neq \left ( x_2 \right )$，都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\forall \lambda \in \left ( 0,1\right )$，则称 f 为强拟凸函数。

定理

如果 $\mathbb{R}^n$ 中非空凸集 S 上的拟凸函数 $f:S\rightarrow \mathbb{R}^n$ 在连接 S 的任意两点的线段上不恒定，则该函数是强拟凸函数。

证明

设 f 是拟凸函数，且它在连接 S 的任意两点的线段上不恒定。

假设 f 不是强拟凸函数。

存在 $x_1,x_2 \in S$ 且 $x_1 \neq x_2$，使得

$$f\left ( z \right )\geq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}, \forall z= \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \in \left ( 0,1 \right )$$

$\Rightarrow f\left ( x_1 \right )\leq f\left ( z \right )$ 且 $f\left ( x_2 \right )\leq f\left ( z \right )$

由于 f 在 $\left [ x_1,z \right ]$ 和 $\left [z,x_2 \right ]$ 上不恒定

所以存在 $u \in \left [ x_1,z \right ]$ 和 $v=\left [ z,x_2 \right ]$

$$\Rightarrow u= \mu_1x_1+\left ( 1-\mu_1\right )z,v=\mu_2z+\left ( 1- \mu_2\right )x_2$$

由于 f 是拟凸函数，

$$\Rightarrow f\left ( u \right )\leq max\left \{ f\left ( x_1 \right ),f \left ( z \right ) \right \}=f\left ( z \right )\:\: and \:\:f \left ( v \right ) \leq max \left \{ f\left ( z \right ),f\left ( x_2 \right ) \right \}$$

$$\Rightarrow f\left ( u \right )\leq f\left ( z \right ) \:\: and \:\: f\left ( v \right )\leq f\left ( z \right )$$

$$\Rightarrow max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$$

但 z 是 u 和 v 之间的任意一点，如果其中任何一个相等，则 f 为常数。

因此，$max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$

这与 f 的拟凸性相矛盾，因为 $z \in \left [ u,v \right ]$。

因此，f 是强拟凸函数。

定理

设 $f:S\rightarrow \mathbb{R}^n$，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集。如果 $\hat{x}$ 是局部最优解，则 $\hat{x}$ 是唯一的全局最优解。

证明

由于强拟凸函数也是严格拟凸函数，因此局部最优解是全局最优解。

唯一性 − 设 f 在两点 $u,v \in S$ 处取得全局最优解

$$\Rightarrow f\left ( u \right ) \leq f\left ( x \right ).\forall x \in S\:\: and \:\:f\left ( v \right ) \leq f\left ( x \right ).\forall x \in S$$

如果 u 是全局最优解，则 $f\left ( u \right )\leq f\left ( v \right )$ 且 $f\left ( v \right )\leq f\left ( u\right )\Rightarrow f\left ( u \right )=f\left ( v\right )$

$$f\left ( \lambda u+\left ( 1-\lambda\right )v\right )< max \left \{f\left ( u \right ),f\left ( v \right ) \right \}=f\left ( u \right )$$

这是矛盾的。

因此，只有一个全局最优解。

备注

• 强拟凸函数也是严格拟凸函数。
• 严格凸函数可能是也可能不是强拟凸函数。
• 可微的严格凸函数是强拟凸函数。

伪凸函数

设 $f:S\rightarrow \mathbb{R}$ 是一个可微函数，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集，则如果对于每个 $x_1,x_2 \in S$ 且 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$，都有 $f\left ( x_2 \right )\geq f\left ( x_1 \right )$，或者等价地，如果 $f\left ( x_1 \right )>f\left ( x_2 \right )$，则 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$，则称 f 为伪凸函数。

伪凹函数

设 $f:S\rightarrow \mathbb{R}$ 是一个可微函数，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集，则如果对于每个 $x_1, x_2 \in S$ 且 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$，都有 $f\left ( x_2 \right )\leq f\left ( x_1 \right )$，或者等价地，如果 $f\left ( x_1 \right )>f\left ( x_2 \right )$，则 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )>0$，则称 f 为伪凹函数。

备注

• 如果一个函数既是伪凸函数又是伪凹函数，则称其为伪线性函数。

• 可微凸函数也是伪凸函数。

• 伪凸函数可能不是凸函数。例如，

  $f\left ( x \right )=x+x^3$ 不是凸函数。如果 $x_1 \leq x_2,x_{1}^{3} \leq x_{2}^{3}$

  因此，$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )=\left ( 1+3x_{1}^{2} \right )\left ( x_2-x_1 \right ) \geq 0$

  并且，$f\left ( x_2 \right )-f\left ( x_1 \right )=\left ( x_2-x_1 \right )+\left ( x_{2}^{3} -x_{1}^{3}\right )\geq 0$

  $\Rightarrow f\left ( x_2 \right )\geq f\left ( x_1 \right )$

  因此，它是伪凸函数。

  伪凸函数是严格拟凸函数。因此，伪凸函数的每个局部最小值也是全局最小值。

严格伪凸函数

设 $f:S\rightarrow \mathbb{R}$ 是一个可微函数，且 S 是 $\mathbb{R}^n$ 中的一个非空凸集，则如果对于每个 $x_1,x_2 \in S$ 且 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$，都有 $f\left ( x_2 \right )> f\left ( x_1 \right )$，或者等价地，如果 $f\left ( x_1 \right )\geq f\left ( x_2 \right )$，则 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$，则称 f 为严格伪凸函数。

定理

设 f 是伪凸函数，并假设对于某个 $\hat{x} \in S$，$\bigtriangledown f\left ( \hat{x}\right )=0$，则 $\hat{x}$ 是 f 在 S 上的全局最优解。

证明

设 $\hat{x}$ 是 f 的临界点，即 $\bigtriangledown f\left ( \hat{x}\right )=0$

由于 f 是伪凸函数，对于 $x \in S,$ 我们有

$$\bigtriangledown f\left ( \hat{x}\right )\left ( x-\hat{x}\right )=0 \Rightarrow f\left ( \hat{x}\right )\leq f\left ( x\right ), \forall x \in S$$

因此，$\hat{x}$ 是全局最优解。

备注

如果 f 是严格伪凸函数，则 $\hat{x}$ 是唯一的全局最优解。

定理

如果 f 是 S 上的可微伪凸函数，则 f 既是严格拟凸函数又是拟凸函数。

备注

• 在 $\mathbb{R}^n$ 的开集 S 上定义的两个伪凸函数之和可能不是伪凸函数。

• 设 $f:S\rightarrow \mathbb{R}$ 是一个拟凸函数，且 S 是 $\mathbb{R}^n$ 的一个非空凸子集，则 f 是伪凸函数当且仅当每个临界点都是 f 在 S 上的全局最小值。

• 设 S 是 $\mathbb{R}^n$ 的一个非空凸子集，且 $f:S\rightarrow \mathbb{R}$ 是一个函数，使得对于每个 $x \in S$，$\bigtriangledown f\left ( x\right )\neq 0$，则 f 是伪凸函数当且仅当它是一个拟凸函数。

凸优化 - 规划问题

凸规划问题有四种类型：

步骤 1 − $min \:f\left ( x \right )$，其中 $x \in S$，S 是 $\mathbb{R}^n$ 中的一个非空凸集，且 $f\left ( x \right )$ 是凸函数。

步骤 2 − $min \: f\left ( x \right ), x \in \mathbb{R}^n$，受以下约束条件限制：

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$，且 $g_i\left ( x \right )$ 是凸函数。

$g_i\left ( x \right ) \leq 0,m_1+1 \leq m_2$，且 $g_i\left ( x \right )$ 是凹函数。

$g_i\left ( x \right ) = 0, m_2+1 \leq m$，且 $g_i\left ( x \right )$ 是线性函数。

其中 $f\left ( x \right )$ 是凸函数。

步骤 3 − $max \:f\left ( x \right )$，其中 $x \in S$，S 是 $\mathbb{R}^n$ 中的一个非空凸集，且 $f\left ( x \right )$ 是凹函数。

步骤 4 − $min \:f\left ( x \right )$，其中 $x \in \mathbb{R}^n$，受以下约束条件限制：

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$，且 $g_i\left ( x \right )$ 是凸函数。

$g_i\left ( x \right ) \leq 0, m_1+1 \leq m_2$，且 $g_i\left ( x \right )$ 是凹函数。

$g_i\left ( x \right ) = 0,m_2+1 \leq m$，且 $g_i\left ( x \right )$ 是线性函数。

其中 $f\left ( x \right )$ 是凹函数。

可行方向锥

设 S 是 $\mathbb{R}^n$ 中的一个非空集，且设 $\hat{x} \in \:Closure\left ( S \right )$，则 S 在 $\hat{x}$ 处的可行方向锥，记为 D，定义为 $D=\left \{ d:d\neq 0,\hat{x}+\lambda d \in S, \lambda \in \left ( 0, \delta \right ), \delta > 0 \right \}$

每个非零向量 $d \in D$ 称为可行方向。

对于给定函数 $f:\mathbb{R}^n \Rightarrow \mathbb{R}$，$\hat{x}$ 处的改进方向锥记为 F，且由下式给出：

$$F=\left \{ d:f\left ( \hat{x}+\lambda d \right )\leq f\left ( \hat{x} \right ),\forall \lambda \in \left ( 0,\delta \right ), \delta >0 \right \}$$

每个方向 $d \in F$ 称为 f 在 $\hat{x}$ 处的改进方向或下降方向。

定理

必要条件

考虑问题 $min f\left ( x \right )$，满足 $x \in S$，其中 S 是 $\mathbb{R}^n$ 中的非空集。假设 f 在点 $\hat{x} \in S$ 处可微。如果 $\hat{x}$ 是局部最优解，则 $F_0 \cap D= \phi$，其中 $F_0=\left \{ d:\bigtriangledown f\left ( \hat{x} \right )^T d < 0 \right \}$ 且 D 是可行方向锥。

充分条件

如果 $F_0 \cap D= \phi$，f 是在 $\hat{x}$ 处的伪凸函数，并且存在 $\hat{x}$ 的邻域 $N_\varepsilon \left ( \hat{x} \right ), \varepsilon > 0$，使得对于任意 $x \in S \cap N_\varepsilon \left ( \hat{x} \right )$，都有 $d=x-\hat{x}\in D$，则 $\hat{x}$ 是局部最优解。

证明

必要条件

令 $F_0 \cap D\neq \phi$，即存在一个 $d \in F_0 \cap D$，使得 $d \in F_0$ 且 $d\in D$

由于 $d \in D$，因此存在 $\delta_1 >0$，使得 $\hat{x}+\lambda d \in S, \lambda \in \left ( 0,\delta_1 \right ).$

由于 $d \in F_0$，因此 $\bigtriangledown f \left ( \hat{x}\right )^T d <0$

因此，存在 $\delta_2>0$，使得 $f\left ( \hat{x}+\lambda d\right )< f\left ( \hat{x}\right ),\forall \lambda \in f \left ( 0,\delta_2 \right )$

令 $\delta=min \left \{\delta_1,\delta_2 \right \}$

则 $\hat{x}+\lambda d \in S, f\left (\hat{x}+\lambda d \right ) < f\left ( \hat{x} \right ),\forall \lambda \in f \left ( 0,\delta \right )$

但 $\hat{x}$ 是局部最优解。

因此，这是一个矛盾。

因此 $F_0\cap D=\phi$

充分条件

令 $F_0 \cap D\neq \phi$ 且令 f 为伪凸函数。

令存在 $\hat{x}$ 的邻域 $N_{\varepsilon}\left ( \hat{x} \right )$，使得 $d=x-\hat{x}, \forall x \in S \cap N_\varepsilon\left ( \hat{x} \right )$

令 $\hat{x}$ 不是局部最优解。

因此，存在 $\bar{x} \in S \cap N_\varepsilon \left ( \hat{x} \right )$，使得 $f \left ( \bar{x} \right )< f \left ( \hat{x} \right )$

根据 $S \cap N_\varepsilon \left ( \hat{x} \right )$ 的假设，$d=\left ( \bar{x}-\hat{x} \right )\in D$

根据 f 的伪凸性，

$$f\left ( \hat{x} \right )>f\left ( \bar{x} \right )\Rightarrow \bigtriangledown f\left ( \hat{x} \right )^T\left ( \bar{x}-\hat{x} \right )<0$$

$\Rightarrow \bigtriangledown f\left ( \hat{x} \right) ^T d <0$

$\Rightarrow d \in F_0$

因此 $F_0\cap D \neq \phi$

这是矛盾的。

因此，$\hat{x}$ 是局部最优解。

考虑以下问题：$min \:f\left ( x\right )$，其中 $x \in X$ 满足 $g_x\left ( x\right ) \leq 0, i=1,2,...,m$

$f:X \rightarrow \mathbb{R},g_i:X \rightarrow \mathbb{R}^n$ 且 X 是 $\mathbb{R}^n$ 中的开集

令 $S=\left \{x:g_i\left ( x\right )\leq 0,\forall i \right \}$

令 $\hat{x} \in X$，则 $M=\left \{1,2,...,m \right \}$

令 $I=\left \{i:g_i\left ( \hat{x}\right )=0, i \in M\right \}$，其中 I 称为 $\hat{x}$ 处所有活动约束的指标集

令 $J=\left \{i:g_i\left ( \hat{x}\right )<0,i \in M\right \}$，其中 J 称为 $\hat{x}$ 处所有非活动约束的指标集。

令 $F_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown f\left ( \hat{x} \right )^T d <0 \right \}$

令 $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gI\left ( \hat{x} \right )^T d <0 \right \}$

或 $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gi\left ( \hat{x} \right )^T d <0 ,\forall i \in I \right \}$

引理

如果 $S=\left \{ x \in X:g_i\left ( x\right ) \leq 0, \forall i \in I\right \}$ 且 X 是 $\mathbb{R}^n$ 中的非空开集。令 $\hat{x}\in S$ 且 $g_i$ 在 $\hat{x}, i \in I$ 处可微，且 $g_i$ 在 $\hat{x}$ 处连续，其中 $i \in J$，则 $G_0 \subseteq D$。

证明

令 $d \in G_0$

由于 $\hat{x} \in X$ 且 X 是开集，因此存在 $\delta_1 >0$，使得对于 $\lambda \in \left ( 0, \delta_1\right )$，都有 $\hat{x}+\lambda d \in X$

同样，由于 $g_\hat{x}<0$ 且 $g_i$ 在 $\hat{x}, \forall i \in J$ 处连续，因此存在 $\delta_2>0$，使得 $g_i\left ( \hat{x}+\lambda d\right )<0, \lambda \in \left ( 0, \delta_2\right )$

由于 $d \in G_0$，因此，$\bigtriangledown g_i\left ( \hat{x}\right )^T d <0, \forall i \in I$，因此存在 $\delta_3 >0, g_i\left ( \hat{x}+\lambda d\right )< g_i\left ( \hat{x}\right )=0$，对于 $\lambda \in \left ( 0, \delta_3\right ) i \in J$

令 $\delta=min\left \{ \delta_1, \delta_2, \delta_3 \right \}$

因此，$\hat{x}+\lambda d \in X, g_i\left ( \hat{x}+\lambda d\right )< 0, i \in M$

$\Rightarrow \hat{x}+\lambda d \in S$

$\Rightarrow d \in D$

$\Rightarrow G_0 \subseteq D$

因此得证。

定理

必要条件

令 f 和 $g_i, i \in I$ 在 $\hat{x} \in S$ 处可微，且 $g_j$ 在 $\hat{x} \in S$ 处连续。如果 $\hat{x}$ 是 S 的局部极小值点，则 $F_0 \cap G_0=\phi$。

充分条件

如果 $F_0 \cap G_0= \phi$ 且 f 是在 $\left (\hat{x}, g_i 9x \right ), i \in I$ 处的伪凸函数，且 $g_i$ 是在 $\hat{x}$ 的某个 $\varepsilon$ -邻域上严格伪凸函数，则 $\hat{x}$ 是局部最优解。

备注

• 令 $\hat{x}$ 为一个可行点，使得 $\bigtriangledown f\left(\hat{x} \right)=0$，则 $F_0 = \phi$。因此，$F_0 \cap G_0= \phi$，但 $\hat{x}$ 不是最优解

• 但如果 $\bigtriangledown g\left(\hat{x} \right)=0$，则 $G_0=\phi$，因此 $F_0 \cap G_0= \phi$

• 考虑问题：min $f\left(x \right)$ 满足 $g\left(x \right)=0$。

  由于 $g\left(x \right)=0$，因此 $g_1\left(x \right)=g\left(x \right)<0$ 且 $g_2\left(x \right)=-g\left(x \right) \leq 0$。

  令 $\hat{x} \in S$，则 $g_1\left(\hat{x} \right)=0$ 且 $g_2\left(\hat{x} \right)=0$。

  但 $\bigtriangledown g_1\left(\hat{x} \right)= - \bigtriangledown g_2\left(\hat{x}\right)$

  因此，$G_0= \phi$ 且 $F_0 \cap G_0= \phi$。

凸优化 - Fritz-John 条件

必要条件

定理

考虑问题 − $min f\left ( x \right )$，满足 $x \in X$，其中 X 是 $\mathbb{R}^n$ 中的开集，且令 $g_i \left ( x \right ) \leq 0, \forall i =1,2,....m$。

令 $f:X \rightarrow \mathbb{R}$ 且 $g_i:X \rightarrow \mathbb{R}$

令 $\hat{x}$ 为可行解，且令 f 和 $g_i, i \in I$ 在 $\hat{x}$ 处可微，且 $g_i, i \in J$ 在 $\hat{x}$ 处连续。

如果 $\hat{x}$ 在局部上解决了上述问题，则存在 $u_0, u_i \in \mathbb{R}, i \in I$，使得 $u_0 \bigtriangledown f\left ( \hat{x} \right )+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i \left ( \hat{x} \right )$=0

其中 $u_0,u_i \geq 0,i \in I$ 且 $\left ( u_0, u_I \right ) \neq \left ( 0,0 \right )$

此外，如果 $g_i,i \in J$ 在 $\hat{x}$ 处也可微，则上述条件可以写成 −

$u_0 \bigtriangledown f\left ( \hat{x}\right )+\displaystyle\sum\limits_{i=1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right )=0$

$u_ig_i\left (\hat{x} \right )$=0

$u_0,u_i \geq 0, \forall i=1,2,....,m$

$\left (u_0,u \right ) \neq \left ( 0,0 \right ), u=\left ( u_1,u_2,s,u_m \right ) \in \mathbb{R}^m$

备注

• $u_i$ 称为拉格朗日乘子。

• $\hat{x}$ 满足给定问题的可行性条件称为原始可行性条件。

• 要求 $u_0 \bigtriangledown f\left (\hat{x} \right )+\displaystyle\sum\limits_{i=1}^m u-i \bigtriangledown g_i\left ( x \right )=0$ 称为对偶可行性条件。

• 条件 $u_ig_i\left ( \hat{x} \right )=0, i=1, 2, ...m$ 称为互补松弛条件。此条件要求 $u_i=0, i \in J$

• 原始可行性条件、对偶可行性条件和互补松弛条件一起称为 Fritz-John 条件。

充分条件

定理

如果存在 $\hat{x}$ 的 $\varepsilon$-邻域 $N_\varepsilon \left ( \hat{x} \right ),\varepsilon >0$，使得 f 在 $N_\varepsilon \left ( \hat{x} \right )\cap S$ 上是伪凸的，且 $g_i,i \in I$ 在 $N_\varepsilon \left ( \hat{x}\right )\cap S$ 上是严格伪凸的，则 $\hat{x}$ 是上述问题的一个局部最优解。如果 f 在 $\hat{x}$ 处是伪凸的，且如果 $g_i, i \in I$ 在 $\hat{x}$ 处既是严格伪凸函数又是拟凸函数，则 $\hat{x}$ 是上述问题的一个全局最优解。

示例

• $min \:f\left ( x_1,x_2 \right )=\left ( x_1-3 \right )^2+\left ( x_2-2 \right )^2$

  满足 $x_{1}^{2}+x_{2}^{2} \leq 5, x_1+2x_2 \leq 4, x_1,x_2 \geq 0$ 且 $\hat{x}=\left ( 2,1 \right )$

  令 $g_1\left (x_1,x_2 \right )=x_{1}^{2}+x_{2}^{2} -5,$

  $g_2\left (x_1,x_2 \right )=x_1+2x_2-4,$

  $g_3\left (x_1,x_2 \right )=-x_1$ 且 $g_4\left ( x_1, x_2 \right )= -x_2$。

  因此，上述约束可以写成 −

  $g_1\left (x_1,x_2 \right )\leq 0,$

  $g_2\left (x_1,x_2 \right )\leq 0,$

  $g_3\left (x_1,x_2 \right )\leq 0$ 且

  $g_4\left (x_1,x_2 \right )\leq 0$ 因此，$I = \left \{1,2 \right \}$，因此，$u_3=0,u_4=0$

  $\bigtriangledown f \left (\hat{x} \right )=\left (2,-2 \right ),\bigtriangledown g_1\left (\hat{x} \right )=\left (4,2 \right )$ 且 $\bigtriangledown g_2\left (\hat{x} \right )=\left (1,2 \right )$

  因此，将这些值代入 Fritz-John 条件的第一条件，得到 −

  $u_0=\frac{3}{2} u_2, \:\:u_1= \frac{1}{2}u_2,$ 且令 $u_2=1$，因此 $u_0= \frac{3}{2},\:\:u_1= \frac{1}{2}$

  因此，Fritz John 条件得到满足。

• $min f\left (x_1,x_2\right )=-x_1$。

  满足 $x_2-\left (1-x_1\right )^3 \leq 0$，

  $-x_2 \leq 0$ 且 $\hat{x}=\left (1,0\right )$

  令 $g_1\left (x_1,x_2 \right )=x_2-\left (1-x_1\right )^3$，

  $g_2\left (x_1,x_2 \right )=-x_2$

  因此，上述约束可以写成 −

  $g_1\left (x_1,x_2 \right )\leq 0,$

  $g_2\left (x_1,x_2 \right )\leq 0,$

  因此，$I=\left \{1,2 \right \}$

  $\bigtriangledown f\left (\hat{x} \right )=\left (-1,0\right )$

  $\bigtriangledown g_1 \left (\hat{x} \right )=\left (0,1\right )$ 且 $g_2 \left (\hat{x} \right )=\left (0, -1 \right )$

  因此，将这些值代入 Fritz-John 条件的第一条件，得到 −

  $u_0=0,\:\: u_1=u_2=a>0$

  因此，Fritz John 条件得到满足。

Karush-Kuhn-Tucker最优性必要条件

考虑问题 −

$min \:f\left ( x \right )$ 满足 $x \in X$，其中 X 是 $\mathbb{R}^n$ 中的开集，且 $g_i \left ( x \right )\leq 0, i=1, 2,...,m$

令 $S=\left \{ x \in X:g_i\left ( x \right )\leq 0, \forall i \right \}$

令 $\hat{x} \in S$，且令 f 和 $g_i,i \in I$ 在 $\hat{x}$ 处可微，且 $g_i, i \in J$ 在 $\hat{x}$ 处连续。此外，$\bigtriangledown g_i\left ( \hat{x} \right), i \in I$ 线性无关。如果 $\hat{x}$ 在局部上解决了上述问题，则存在 $u_i,i \in I$，使得

$\bigtriangledown f\left ( x\right)+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$, $\:\:u_i \geq 0, i \in I$

如果 $g_i,i \in J$ 在 $\hat{x}$ 处也可微，则

$\bigtriangledown f\left ( \hat{x}\right)+\displaystyle\sum\limits_{i= 1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$

$u_ig_i\left ( \hat{x} \right)=0, \forall i=1,2,...,m$

$u_i \geq 0 \forall i=1,2,...,m$

示例

考虑以下问题 -

$min \:f\left ( x_1,x_2 \right )=\left ( x_1-3\right )^2+\left ( x_2-2\right )^2$

使得 $x_{1}^{2}+x_{2}^{2}\leq 5$，

$x_1,2x_2 \geq 0$ 且 $\hat{x}=\left ( 2,1 \right )$

令 $g_1\left ( x_1, x_2 \right)=x_{1}^{2}+x_{2}^{2}-5$，

$g_2\left ( x_1, x_2 \right)=x_{1}+2x_2-4$

$g_3\left ( x_1, x_2 \right)=-x_{1}$ 且 $g_4\left ( x_1,x_2 \right )=-x_2$

因此，上述约束可以写成 −

$g_1 \left ( x_1,x_2 \right)\leq 0, g_2 \left ( x_1,x_2 \right) \leq 0$

$g_3 \left ( x_1,x_2 \right)\leq 0,$ 且 $g_4 \left ( x_1,x_2 \right) \leq 0$ 因此，$I=\left \{ 1,2 \right \}$，所以， $u_3=0,\:\: u_4=0$

$\bigtriangledown f \left ( \hat{x} \right)=\left ( 2,-2 \right), \bigtriangledown g_1 \left ( \hat{x} \right)= \left ( 4,2 \right)$ 且

$\bigtriangledown g_2\left ( \hat{x} \right ) =\left ( 1,2 \right )$

因此，将这些值代入 Karush-Kuhn-Tucker 条件的第一条件，得到 -

$u_1=\frac{1}{3}$ 且 $u_2=\frac{2}{3}$

因此，Karush-Kuhn-Tucker 条件满足。

凸问题的算法

最速下降法

此方法也称为梯度法或柯西法。此方法涉及以下术语 -

$$x_{k+1}=x_k+\alpha_kd_k$$

$d_k= - \bigtriangledown f\left ( x_k \right )$ 或 $d_k= -\frac{\bigtriangledown f\left ( x_k \right )}{\left \| \bigtriangledown f\left ( x_k \right ) \right \|}$

令 $\phi \left (\alpha \right )=f\left ( x_k +\alpha d_k\right )$

通过对 $\phi$ 求导并使其等于零，我们可以得到 $\alpha$。

因此，算法如下 -

• 初始化 $x_0$，$\varepsilon_1$，$\varepsilon_2$ 并设置 $k=0$。

• 设置 $d_k=-\bigtriangledown f\left ( x_k \right )$或 $d_k=-\frac{\bigtriangledown f\left (x_k \right )}{\left \|\bigtriangledown f\left (x_k \right ) \right \|}$。

• 找到 $\alpha_k$ 使其最小化 $\phi\left ( \alpha \right )=f\left ( x_k+\alpha d_k \right )$。

• 设置 $x_{k+1}=x_k+\alpha_kd_k$。

• 如果 $\left \| x_{k+1-x_k} \right \| <\varepsilon_1$ 或 $\left \| \bigtriangledown f\left ( x_{k+1} \right ) \right \| \leq \varepsilon_2$，则转到步骤 6，否则设置 $k=k+1$ 并转到步骤 2。

• 最优解为 $\hat{x}=x_{k+1}$。

牛顿法

牛顿法基于以下原理 -

$f\left ( x \right )=y\left ( x \right )=f\left ( x_k \right )+\left ( x-x_k \right )^T \bigtriangledown f\left ( x_k \right )+\frac{1}{2}\left ( x-x_k \right )^T H\left ( x_k \right )\left ( x-x_k \right )$

$\bigtriangledown y\left ( x \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x-x_k \right )$

在 $x_{k+1}$ 处，$\bigtriangledown y\left ( x_{k+1} \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x_{k+1}-x_k \right )$

为了使 $x_{k+1}$ 为最优解，$\bigtriangledown y\left ( x_k+1 \right )=0$

因此，$x_{k+1}=x_k-H\left ( x_k \right )^{-1} \bigtriangledown f\left ( x_k \right )$

这里 $H\left ( x_k \right )$ 应为非奇异的。

因此，算法如下 -

步骤 1 - 初始化 $x_0$，$\varepsilon$ 并设置 $k=0$。

步骤 2 - 找到 $H\left ( x_k \right ) \bigtriangledown f\left ( x_k \right )$。

步骤 3 - 求解线性系统 $H\left ( x_k \right )h\left ( x_k \right )=\bigtriangledown f\left ( x_k \right )$ 以获得 $h\left ( x_k \right )$。

步骤 4 - 找到 $x_{k+1}=x_k-h\left ( x_k \right )$。

步骤 5 - 如果 $\left \| x_{k+1}-x_k \right \|< \varepsilon$ 或 $\left \| \bigtriangledown f\left ( x_k \right ) \right \| \leq \varepsilon$，则转到步骤 6，否则设置 $k=k+1$ 并转到步骤 2。

步骤 6 - 最优解为 $\hat{x}=x_{k+1}$。

共轭梯度法

此方法用于解决以下类型的問題 -

$min f\left ( x \right )=\frac{1}{2}x^T Qx-bx$

其中 Q 是一个正定 nXn 矩阵，b 是常数。

给定 $x_0$，$\varepsilon$，计算 $g_0=Qx_0-b$

设置 $d_0=-g_0$，对于 $k=0,1,2,...,$

设置 $\alpha_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Q d_k}$

计算 $x_{k+1}=x_k+\alpha_kd_k$

设置 $g_{k+1}=g_k+\alpha_kd_k$

计算 $\beta_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Qd_k}$

计算 $x_{k+1}=x_k+\alpha_kd_k$

设置 $g_{k+1}=x_k+\alpha_kQd_k$

计算 $\beta_k=\frac{g_{k+1}^{T}g_{k+1}}{g_{k}^{T}gk}$

设置 $d_{k+1}=-g_{k+1}+\beta_kd_k$。