ABCD是一个矩形，其中对角线AC平分∠A和∠C。证明：(i) ABCD是正方形 (ii) 对角线BD平分∠B和∠D。

已知

$ABCD$是一个矩形，其中对角线$AC$平分∠A和∠C。

要求

我们需要证明

(i) $ABCD$是正方形

(ii) 对角线$BD$平分∠B和∠D。

解答

(i) 当所有边都相等时，正方形是矩形。

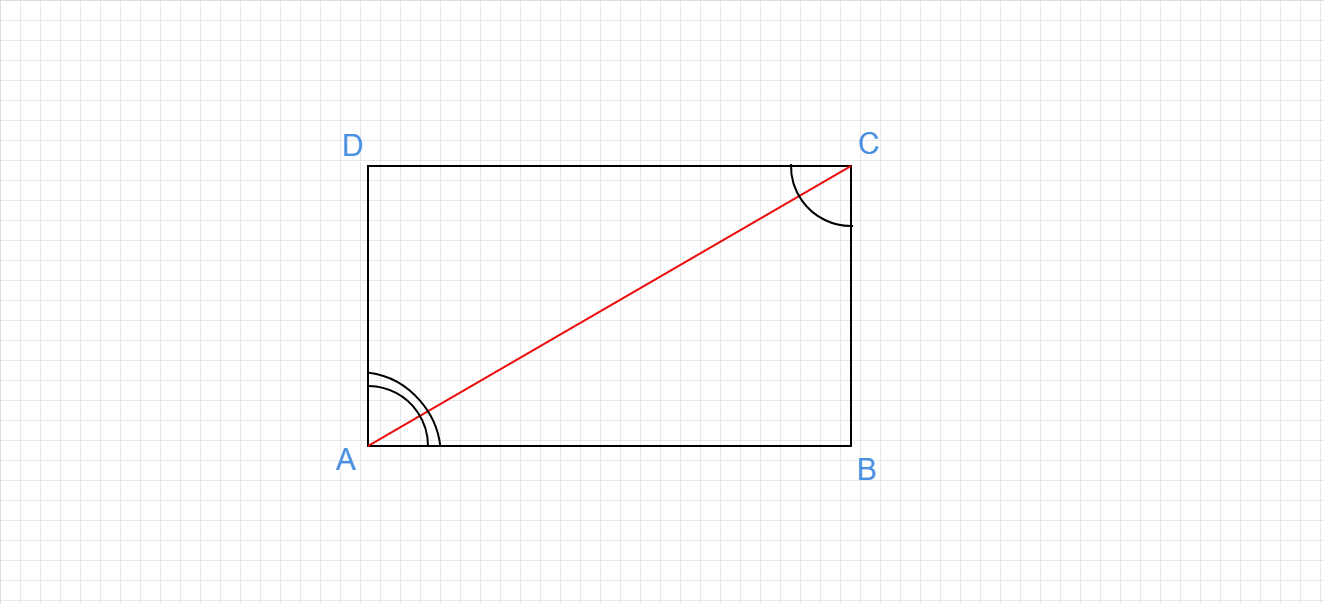
在上图中，$AC$平分∠A和∠C。

因此，

$\angle DAC = \angle BAC$............(i)

$\angle DCA = \angle BCA$............(ii)

在矩形中，对边平行。

所以，$AD \parallel BC$

$AC$是截线。

因此，

$\angle DAC = \angle BCA$...........(iii)                      [内错角]

由(i)和(iii)，

$\angle BCA = \angle BAC$..........(iv)

在$\Delta ABC$中，

$\angle BCA = \angle BAC$

所以，$AB = BC$...........(v)

我们已经知道，

在矩形$ABCD$中，$AB = CD, BC = DA$.............(vi)

由(v)和(vi)，

$AB = BC = CD = DA$。

因此，$ABCD$是正方形。

(ii) $ABCD$是正方形，

正方形的对角线平分其角。

因此，对角线$BD$平分∠B和∠D。

证毕。

教程点

更新于： 2022年10月10日

67 次浏览

开启你的职业生涯

完成课程获得认证

开始学习