数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究Arduino上的快速傅里叶变换 (FFT)
有几个可用的库可以帮助您在 Arduino 上计算快速傅里叶变换 (FFT)。我们将研究 **arduinoFFT** 库。此库可以通过库管理器安装（搜索 **arduinoFFT**）。
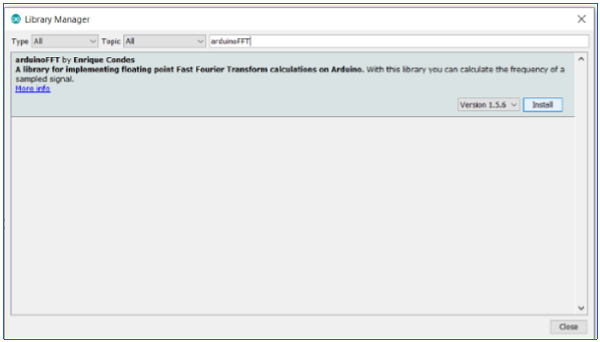
安装完成后，转到：**文件→示例→arduinoFFT** 并打开 **FFT_01** 示例。
示例
此示例首先创建一个频率为 1000Hz 的正弦波（以 5000Hz 采样）。然后使用 **汉明窗函数** 对其进行加窗。之后计算 FFT，确定幅度最大的频率，并将其作为基频返回。如果该值接近 1000 Hz，则此代码有效。
让我们开始代码演练。我们首先包含库并创建 **arduinoFFT()** 对象。
#include "arduinoFFT.h" arduinoFFT FFT = arduinoFFT(); // Create FFT object We then define the variables specific to the signal. const uint16_t samples = 64; //This value MUST ALWAYS be a power of 2 const double signalFrequency = 1000; const double samplingFrequency = 5000; const uint8_t amplitude = 100;
我们将使用信号的 64 个样本生成我们的时域数组。此外，此样本数应始终为 2 的幂。
稍后，我们定义两个数组，分别用于存储 FFT 输出的实部和虚部，以及最初的原始数据。
double vReal[samples]; double vImag[samples];
最后，定义了 4 个常量。这些作为参数传递到稍后定义的 **printVector()** 函数中，并帮助确定缩放因子。当我们遍历 **printVector()** 函数时，我们将看到它们的用法。
#define SCL_INDEX 0x00 #define SCL_TIME 0x01 #define SCL_FREQUENCY 0x02 #define SCL_PLOT 0x03
在 setup 中，我们只需初始化 Serial。
void setup()
{
Serial.begin(115200);
while(!Serial);
Serial.println("Ready");
}在循环中，我们首先构建我们的时域信号数组。
void loop()
{
/* Build raw data */
// Number of signal cycles that the sampling will read
double cycles = (((samples-1) * signalFrequency) / samplingFrequency);
for (uint16_t i = 0; i < samples; i++)
{
/* Build data with positive and negative values*/
vReal[i] = int8_t((amplitude * (sin((i * (twoPi * cycles)) / samples))) / 2.0);
// vReal[i] = uint8_t((amplitude * (sin((i * (twoPi * cycles)) / samples) + 1.0)) / 2.0);
/* Build data displaced on the Y axis to include only positive values*/
/* Imaginary part must be zeroed in case of looping to avoid wrong calculations and overflows */
vImag[i] = 0.0;
}然后我们打印信号，对信号应用汉明窗并再次打印它。然后，我们使用 **FFT.Compute()** 计算 FFT，并打印实部和虚部向量。之后，我们使用 **FFT.ComplexToMagnitude()** 从实部和虚部向量计算幅度，并打印幅度。
最后，我们计算幅度最大的频率（使用 **FFT.majorPeak()**）并打印它。
运行此操作后，幅度最大的频率变为 1004.225670，这非常接近 1000 Hz。
/* Print the results of the simulated sampling according to time */
Serial.println("Data:");
PrintVector(vReal, samples, SCL_TIME);
/* Weigh data */
FFT.Windowing(vReal, samples, FFT_WIN_TYP_HAMMING, FFT_FORWARD);
Serial.println("Weighed data:");
PrintVector(vReal, samples, SCL_TIME);
FFT.Compute(vReal, vImag, samples, FFT_FORWARD); //Compute FFT
Serial.println("Computed Real values:");
PrintVector(vReal, samples, SCL_INDEX);
Serial.println("Computed Imaginary values:");
PrintVector(vImag, samples, SCL_INDEX);
FFT.ComplexToMagnitude(vReal, vImag, samples); // Compute magnitudes
Serial.println("Computed magnitudes:");
PrintVector(vReal, (samples >> 1), SCL_FREQUENCY);
double x = FFT.MajorPeak(vReal, samples, samplingFrequency);
Serial.println(x, 6);
while(1); / * Run Once */
// delay(2000); /* Repeat after delay */
}最后，定义了 **printVector** 函数。
此函数接收要打印的向量、要打印的条目数和缩放因子。
如果因子为 **SCL_INDEX**，则打印向量中每个条目的索引号。
如果因子为 **SCL_TIME**，则从 0 开始打印向量中每个条目的时间（使用采样频率）。如果采样频率为 100，则每次读取需要 1/100 或 0.01 秒。因此，可以计算每次读取的时间。
如果因子为 **SCL_FREQUENCY**，则打印对应于每个条目的频率。请注意，这仅在计算幅度后使用。
PrintVector(vReal, (samples >> 1), SCL_FREQUENCY);
请注意，我们已将样本右移了 1 位。由于样本始终为 2 的幂，因此右移意味着将样本数除以 2。因此，对于 64 个样本，右移 1 位后的值变为 32。
FFT 给出从 0 到 **采样频率/2**（奈奎斯特准则）的频率值。因此，每个索引处的频率值为 **索引*采样频率/样本数**。这就是我们获取频率的方式。
void PrintVector(double *vData, uint16_t bufferSize, uint8_t scaleType)
{
for (uint16_t i = 0; i < bufferSize; i++)
{
double abscissa;
/* Print abscissa value */
switch (scaleType)
{
case SCL_INDEX:
abscissa = (i * 1.0);
break;
case SCL_TIME:
abscissa = ((i * 1.0) / samplingFrequency);
break;
case SCL_FREQUENCY:
abscissa = ((i * 1.0 * samplingFrequency) / samples);
break;
}
Serial.print(abscissa, 6);
if(scaleType==SCL_FREQUENCY)
Serial.print("Hz");
Serial.print(" ");
Serial.println(vData[i], 4);
}
Serial.println();
}请注意，尚未建立计算出的幅度与原始信号幅度之间的关系。建议您仔细阅读此库附带的其他示例。
10K+ 次查看
