数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究如果△ABC的三条边的中点分别为D(-1/2, 5/2), E(7, 3) 和 F(7/2, 7/2)，求△ABC的面积。
已知
D(-1/2, 5/2), E(7, 3) 和 F(7/2, 7/2) 是△ABC三条边的中点。
求解
我们需要求出△ABC的面积。
解题步骤
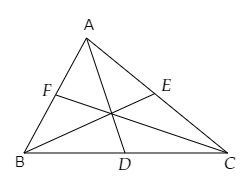
设A(x₁, y₁), B(x₂, y₂) 和 C(x₃, y₃) 是△ABC的顶点。
坐标为(x₁, y₁) 和 (x₂, y₂) 的线段的中点坐标为((x₁+x₂)/2, (y₁+y₂)/2)
D(-1/2, 5/2)是BC的中点。
(x₂+x₃)/2 = -1/2
=> x₂ + x₃ = -1 ......(i)
(y₂+y₃)/2 = 5/2
=> y₂ + y₃ = 5 ......(a)
类似地，
E(7, 3)是CA的中点。
(x₃+x₁)/2 = 7
=> x₃ + x₁ = 14 ......(ii)
(y₃+y₁)/2 = 3
=> y₃ + y₁ = 6 ......(b)
F(7/2, 7/2)是AB的中点。
(x₁+x₂)/2 = 7/2
=> x₁ + x₂ = 7 ......(iii)
(y₁+y₂)/2 = 7/2
=> y₁ + y₂ = 7 ......(c)
将(i), (ii) 和 (iii) 三式相加，得到：
2(x₁ + x₂ + x₃) = 20
=> x₁ + x₂ + x₃ = 10 ......(iv)
分别从(iv)式中减去(i), (ii) 和 (iii)式，得到：
x₁ = 11, x₂ = -4, x₃ = 3
将(a), (b) 和 (c) 三式相加，得到：
2(y₁ + y₂ + y₃) = 18
=> y₁ + y₂ + y₃ = 9 ......(d)
分别从(d)式中减去(a), (b) 和 (c)式，得到：
y₁ = 4, y₂ = 3, y₃ = 2
因此，△ABC的顶点坐标为A(11, 4), B(-4, 3) 和 C(3, 2)
△ABC的面积为：Δ = 1/2[x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)]
Δ = 1/2[11(3-2) + (-4)(2-4) + 3(4-3)]
= 1/2[11×1 + (-4)(-2) + 3(1)]
= 1/2(11 + 8 + 3)
= 22/2
\( =11 \)
△ABC的面积为11平方单位。
浏览量：50
