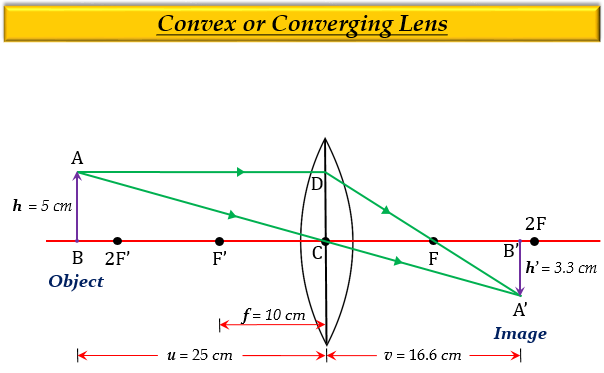
一个高5厘米的物体放在距离焦距为10厘米的会聚透镜25厘米处。求所成像的位置、大小和性质。并画出光路图。

物距，$u$ = $-$25 cm (因为物体总是放置在透镜左侧，所以取负值)

焦距，$f$ = 10 cm

物体高度 $h$ = $+$5 cm

求解：像的位置、性质、$v$ 和像的大小 $h'$。

解答

根据透镜公式，我们知道

$\frac {1}{v}-\frac {1}{u}=\frac {1}{f}$

将已知值代入公式，我们得到：

$\frac {1}{v}-\frac {1}{(-25)}=\frac {1}{10}$

$\frac {1}{v}+\frac {1}{25}=\frac {1}{10}$

$\frac {1}{v}=\frac {1}{10}-\frac {1}{25}$

$\frac {1}{v}=\frac {5-2}{50}$

$\frac {1}{v}=\frac {3}{50}$

$v=\frac {50}{3}$

$v=+16.6\ cm$

因此，像距 $v$ 为 16.6 cm，像距的正号 $(+)$ 表示像形成在 透镜右侧（透镜后）。我们知道，在透镜右侧形成 实像。

现在，

根据放大率公式，我们知道

$m=\frac {v}{u}=\frac {h'}{h}$

将已知值代入公式，我们得到：

$\frac {\frac {50}{3}}{-25}=\frac {h'}{5}$

$\frac {50}{-25\times {3}}=\frac {h'}{5}$

$-\frac {2}{3}=\frac {h'}{5}$

$h'=-\frac {10}{3}$ [交叉相乘]

$h'=-3.3cm$

因此，像的大小 $h'$ 为 3.3 cm，负号 $(-)$ 表示像是 倒立的（在主轴下方）。

因此，像的 位置在 透镜后（右侧），像的 性质是 实像且倒立，像的 大小比物体 小（3.3 cm）。

Tutorialspoint

更新于：2022年10月10日

浏览量：387

启动你的职业生涯

完成课程获得认证

开始学习