一个物体放置在焦距为 30 厘米的凹透镜前 15 厘米处。列出四个特征（性质、位置等）所形成的像由透镜。

物体距离 = $u$ = $-$ 15 cm 

焦距 = $f$ = $-$ 30 cm

求解：四个特征（性质、位置等）由透镜形成的像。

解决方案

使用透镜公式，我们得到 -

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

它可以重新排列为 -

$\frac{1}{v}=\frac{1}{f}+\frac{1}{u}$

代入给定值，我们得到 -

$\frac{1}{v}=\frac{1}{(-30)}+\frac{1}{(-15)}$

$\frac{1}{v}=-\frac{1}{30}-\frac{1}{15}$

$\frac{1}{v}=\frac{-1-2}{30}$

$\frac{1}{v}=-\frac{3}{30}$

$\frac{1}{v}=-\frac{1}{10}$

$v=-10cm$

该四个特征（性质、位置等）所形成的像由透镜是：

1. 形成的像是虚像。

2.像是正立的。

3. 像是缩小的（比物体小）。

4. 像形成在凹透镜光心处 10 厘米处，位于物体同侧。

解释

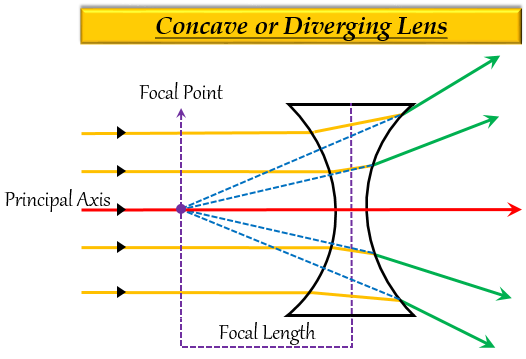
发散透镜或凹透镜 -它是一种至少有一个表面在中间向内弯曲的透镜。换句话说，它在中间较薄，而在上下边缘较厚，因此进入透镜的光会散开或发散，从而形成较小的图像。由于这种效应，它也被称为负透镜或发散透镜。

凹透镜形成的像是虚像和正立的，这意味着它看起来比实际距离更远，因此比物体本身更小。