计算阴影区域的面积：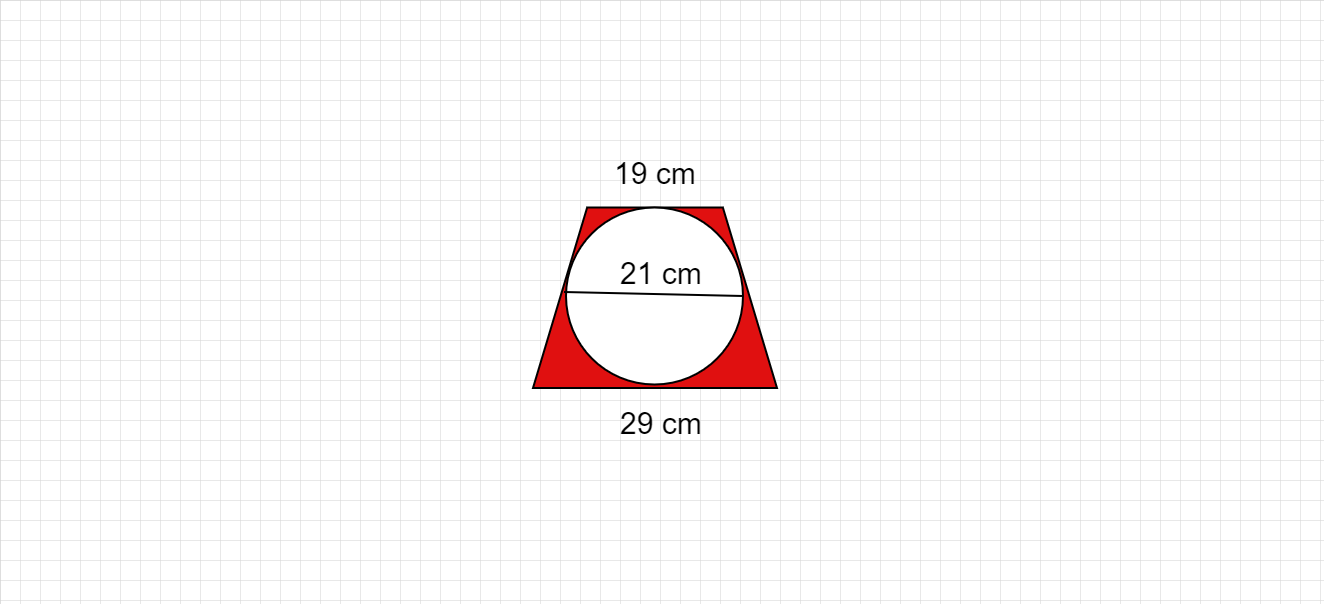

已知

图中显示一个内切于梯形的圆。

求解

我们需要求出阴影区域的面积。

解题过程

外形是一个梯形，其高是圆半径的两倍。

因此，

梯形的面积 $= \frac{1}{2} \times 21 \times (19+29) cm^2$

 

                                        $= \frac{1}{2} \times 21 \times 48  cm^2$

 

                                        $= 21\times24 cm^2$

 

                                       $= 504 cm^2$。

 

内形（圆）的面积 $= π r^2$

内圆直径 $= 21 cm$

圆的半径 $= \frac{21}{2} cm$

圆的面积 $= \frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}$

 

                               $=11\times3\times \frac{21}{2}$

  

                               $=\frac{693}{2} cm^2$

  

                               $= 346.5 cm^2$。

 

阴影部分的面积 = 梯形的面积 - 圆的面积

                                                  $= 504-346.5 cm^2$

                                                  $= 157.5 cm^2$

阴影区域的面积是 $157.5 cm^2$


更新于：2022年10月10日

208 次浏览

启动您的 职业生涯

完成课程获得认证

开始学习
广告