在下图中，阴影区域的边界由四个半圆弧组成，其中最小的两个半圆弧相等。如果最大的半圆弧的直径为$14 \mathrm{~cm}$，最小的半圆弧的直径为$3.5$ $\mathrm{cm}$，求边界的长度。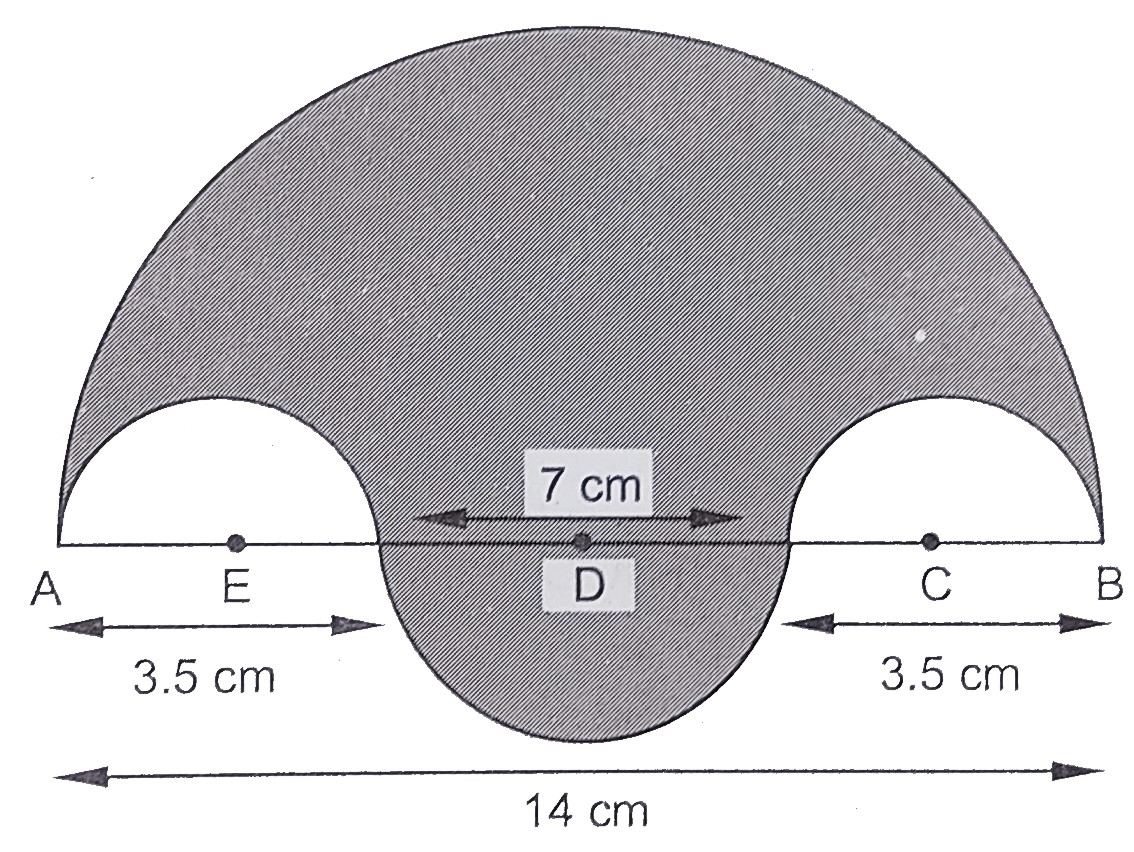

已知

阴影区域的边界由四个半圆弧组成，其中最小的两个半圆弧相等。

最大的半圆弧的直径为$14 \mathrm{~cm}$，最小的半圆弧的直径为$3.5$ $\mathrm{cm}$。

要求：

我们必须找到边界的长度。

解答

最大半圆的直径 = 14 cm

这意味着：

半径 $R =\frac{14}{2}$

$= 7\ cm$
D点半圆的直径 = 7 cm

这意味着：

半径 $r_1 =\frac{7}{2}\ cm$

每个小圆的直径 = 3.5 cm

这意味着：

半径 $r_{2}=\frac{3.5}{2}=1.75 \mathrm{~cm}$

因此：

边界长度 = 最大半圆的周长 + 中间半圆的周长 + 两个小半圆的周长

$=\pi \mathrm{R}+\pi r_{1}+2 \pi r_{2}$

$=\pi(\mathrm{R}+r_{1}+2 r_{2})$

$=\frac{22}{7}(7+3.5+2 \times \frac{3.5}{2})$

$=\frac{22}{7}(7+3.5+3.5)$

$=\frac{22}{7} \times 14$

$=44 \mathrm{~cm}$

边界长度为 44 cm。

Tutorialspoint

更新于：2022年10月10日

48 次浏览

开启你的职业生涯

完成课程获得认证

开始学习