平行四边形的三个连续顶点为(-2, -1)、(1, 0)和(4, 3)。求第四个顶点。

已知

平行四边形的三个连续顶点为(-2, -1)、(1, 0)和(4, 3)。

要求

我们必须找到第四个顶点。

解答

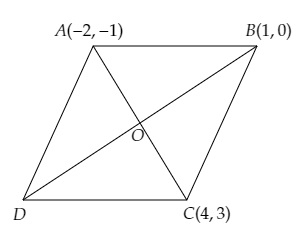
设三个顶点的坐标为A(-2, -1)、B(1, 0)和C(4, 3)。
设第四个顶点为D(x,y)，对角线AC和BD互相平分于点O。

这意味着，

O是AC的中点。

O的坐标为(-2+4)/2, (-1+3)/2)

= (2/2, 2/2)

\( =(1,1) \)

O是BD的中点。

O的坐标为((1+x)/2, (0+y)/2)

因此，

(1,1) = ((1+x)/2, y/2)

比较可得，

(1+x)/2 = 1

1+x = 1(2)

x = 2-1 = 1

类似地，

y/2 = 1

y = 1(2)

y = 2

因此，第四个顶点的坐标为(1,2)。

Tutorialspoint

更新于：2022年10月10日

62 次浏览

开启你的职业生涯

完成课程获得认证

开始学习