Processing math: 100%

两根等高杆子分别立在一条宽为 $80\ m$ 的道路的两侧，相对而立。从道路上它们之间的一点，观察到两根杆子顶端的仰角分别为 $60^{o}$ 和 $30^{o}$ 。求杆子的高度以及这一点到两根杆子的距离。

学术数学 NCERT 10 年级

已知：两根等高的杆子

$AB$ 和

$CD$ ，设

$AB=CD=h$ ，两根杆子之间的距离

$BD=80\ m$

要求：求杆子的高度以及这一点到两根杆子的距离。

解

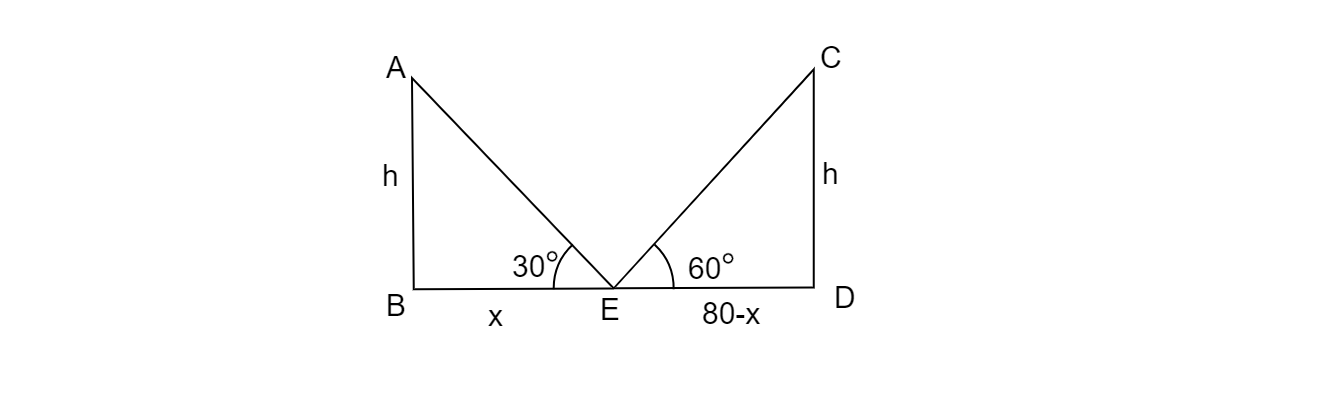
设这一点为

$E$ ，使得

$BE=x$ ，

$ED=80−x$

在

$\vartriangle ABE$ 中

$tan30^{o}=\frac{AB}{BE}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{x}$

$\Rightarrow x=\sqrt{3}h$ .........

$( 1)$

在

$\vartriangle CED$ 中

$tan60^{o}=\frac{CD}{ED}$

$\sqrt{3}=\frac{h}{80-x}$

$\Rightarrow h=( 80-x)\sqrt{3}$ .........

$( 2)$

将x的值代入方程

$( 2)$ ，得到

$h=( 80-\sqrt{3}h)\sqrt{3}$

$\Rightarrow h=80\sqrt{3}-3h$

$\Rightarrow h+3h=80\sqrt{3}$

$\Rightarrow 4h =80\sqrt{3}$

$\Rightarrow h=\frac{80\sqrt{3}}{4}$

$\Rightarrow h=20\sqrt{3}\ m$

由

$( 1)$ ，我们知道

$x=h\sqrt{3}$

$\Rightarrow x=20\sqrt{3}\times\sqrt{3}$

$\Rightarrow x=60\ m$

$\therefore DE=80-x=80-60=20\ m$

因此，每根杆子的高度为

$20\sqrt{3}\ m$ ，这一点到两根杆子的距离分别为

$60\ m$ 和

$20\ m$ 。

教程点

更新于： 2022年10月10日

59 次浏览

开启你的职业生涯

完成课程，获得认证

广告