Plotly - 箱线图、小提琴图和等高线图

上一页
下一页

本章重点介绍各种图表的详细理解，包括箱线图、小提琴图、等高线图和矢羽图。首先，我们将从箱线图开始。

箱线图

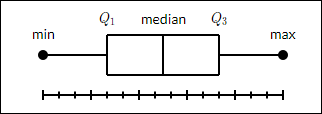
箱线图显示一组数据的摘要，包含最小值、**第一四分位数、中位数、第三四分位数**和**最大值**。在箱线图中，我们从第一四分位数到第三四分位数绘制一个箱体。一条垂直线穿过箱体上的中位数。从箱体垂直延伸出去，指示上、下四分位数之外变异性的线称为须线。因此，箱线图也称为箱须图。须线从每个四分位数延伸到最小值或最大值。

Box Plot

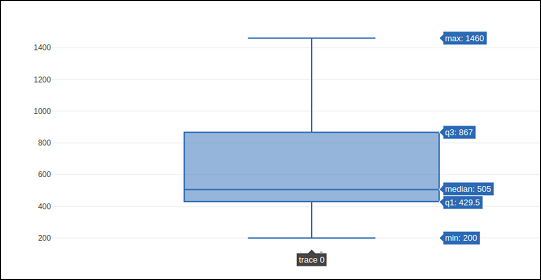
要绘制箱形图，我们必须使用**go.Box()**函数。数据系列可以分配给x或y参数。相应地，箱线图将水平或垂直绘制。在下面的示例中，某公司各个分支机构的销售数据被转换为水平箱线图。它显示了最小值和最大值的中间值。

trace1 = go.Box(y = [1140,1460,489,594,502,508,370,200])
data = [trace1]
fig = go.Figure(data)
iplot(fig)

其输出如下所示：

BoxPoints Parameter

**go.Box()**函数可以赋予各种其他参数来控制箱线图的外观和行为。其中之一是boxmean参数。

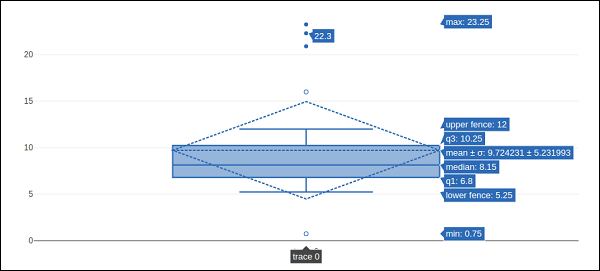
**boxmean**参数默认设置为true。因此，箱体底层分布的均值在箱体内部以虚线的形式绘制。如果将其设置为sd，则还会绘制分布的标准差。

**boxpoints**参数默认等于“**outliers**”。仅显示位于须线之外的样本点。如果“suspectedoutliers”，则显示异常值点，并且小于4“Q1-3”Q3或大于4“Q3-3”Q1的点会被突出显示。如果“False”，则仅显示箱体，不显示样本点。

在下面的示例中，**箱体轨迹**以标准差和异常值点的形式绘制。

trc = go.Box(
   y = [
      0.75, 5.25, 5.5, 6, 6.2, 6.6, 6.80, 7.0, 7.2, 7.5, 7.5, 7.75, 8.15,
      8.15, 8.65, 8.93, 9.2, 9.5, 10, 10.25, 11.5, 12, 16, 20.90, 22.3, 23.25
   ],
   boxpoints = 'suspectedoutliers', boxmean = 'sd'
)
data = [trc]
fig = go.Figure(data)
iplot(fig)

其输出如下所示：

Box Trace

小提琴图

小提琴图类似于箱线图，不同之处在于它们还显示了数据在不同值处的概率密度。小提琴图将包含数据中位数的标记以及表示四分位数间距的箱体，就像标准箱线图一样。叠加在这个箱线图上的是一个核密度估计。与箱线图一样，小提琴图用于表示不同“类别”中变量分布（或样本分布）的比较。

小提琴图比简单的箱线图提供了更多信息。事实上，箱线图仅显示均值/中位数和四分位数间距等汇总统计量，而小提琴图显示了**数据的完整分布**。

**graph_objects**模块中的**go.Violin()**函数返回小提琴图轨迹对象。为了显示底层的箱线图，将**boxplot_visible**属性设置为True。类似地，通过将**meanline_visible**属性设置为true，在小提琴图内部显示一条对应于样本均值的线。

以下示例演示了如何使用Plotly的功能显示小提琴图。

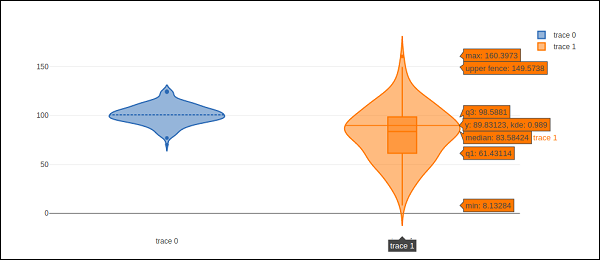
import numpy as np
np.random.seed(10)
c1 = np.random.normal(100, 10, 200)
c2 = np.random.normal(80, 30, 200)
trace1 = go.Violin(y = c1, meanline_visible = True)
trace2 = go.Violin(y = c2, box_visible = True)
data = [trace1, trace2]
fig = go.Figure(data = data)
iplot(fig)

输出如下所示：

Violin Plot

等高线图

二维等高线图显示二维数值数组z的等高线，即z的**等值线**的插值线。函数两个变量的等高线是函数值恒定的曲线，因此曲线连接等值点。

如果您想查看某个值Z如何随两个输入**X**和**Y**的变化而变化，则等高线图是合适的，使得**Z = f(X,Y)**。函数两个变量的等高线或等值线是函数值恒定的曲线。

自变量x和y通常限制在一个称为网格的规则网格中。numpy.meshgrid根据x值数组和y值数组创建一个矩形网格。

让我们首先使用Numpy库中的**linspace()**函数为x、y和z创建数据值。我们从x和y值创建**网格**，并获得由**x2+y2**的平方根组成的z数组。

我们在**graph_objects**模块中具有**go.Contour()**函数，它接受x、**y**和**z**属性。以下代码片段显示了如上计算的x、**y**和**z**值的等高线图。

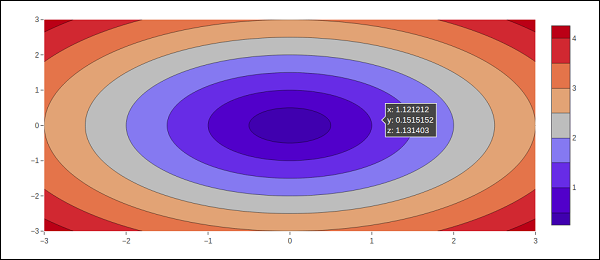
import numpy as np
xlist = np.linspace(-3.0, 3.0, 100)
ylist = np.linspace(-3.0, 3.0, 100)
X, Y = np.meshgrid(xlist, ylist)
Z = np.sqrt(X**2 + Y**2)
trace = go.Contour(x = xlist, y = ylist, z = Z)
data = [trace]
fig = go.Figure(data)
iplot(fig)

输出如下所示：

Contour Plot

等高线图可以通过以下一个或多个参数进行自定义：

  • **转置（布尔值）** - 转置z数据。

如果**xtype**（或**ytype**）等于“array”，则x/y坐标由“x”/“y”给出。如果“scaled”，则x坐标由“x0”和“**dx**”给出。

  • **connectgaps**参数决定是否填充z数据中的间隙。

  • **ncontours**参数的默认值为15。实际的等高线数量将自动选择，使其小于或等于`ncontours`的值。仅当`autocontour`为“True”时有效。

等高线类型默认为：“**levels**”，因此数据表示为具有多个级别显示的等高线图。如果**constrain**，则数据表示为约束，无效区域的阴影由**operation**和**value**参数指定。

**showlines** - 确定是否绘制等高线。

**zauto**默认为**True**，并确定颜色域是根据输入数据（此处为`z`）计算，还是根据`**zmin**`和`**zmax**`中设置的边界计算。当用户设置`zmin`和`zmax`时，默认为`**False**`。

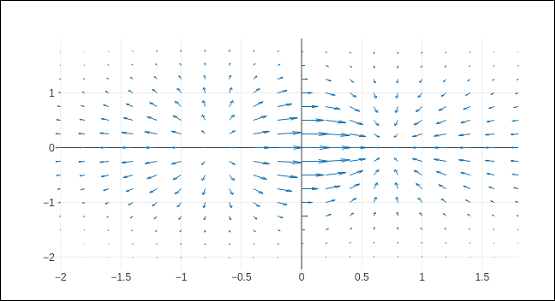
矢羽图

矢羽图也称为**速度图**。它以箭头形式显示速度矢量，其分量为（**u,v**），位于点（x,y）处。为了绘制矢羽图，我们将使用Plotly中**figure_factory**模块中定义的**create_quiver()**函数。

Plotly的Python API包含一个figure factory模块，其中包含许多包装函数，这些函数创建了Plotly的开源绘图库**plotly.js**中尚未包含的独特图表类型。

create_quiver()函数接受以下参数：

  • **x** - 箭头的x坐标

  • **y** - 箭头的y坐标

  • **u** - 箭头矢量的x分量

  • **v** - 箭头矢量的y分量

  • **scale** - 缩放箭头的尺寸

  • **arrow_scale** - 箭头头的长度。

  • **angle** - 箭头头的角度。

以下代码在Jupyter Notebook中呈现一个简单的矢羽图：

import plotly.figure_factory as ff
import numpy as np
x,y = np.meshgrid(np.arange(-2, 2, .2), np.arange(-2, 2, .25))
z = x*np.exp(-x**2 - y**2)
v, u = np.gradient(z, .2, .2)

# Create quiver figure
fig = ff.create_quiver(x, y, u, v,
scale = .25, arrow_scale = .4,
name = 'quiver', line = dict(width = 1))
iplot(fig)

代码的输出如下所示：

Quiver Plot
打印页面
上一页
下一页
广告