如图所示，与三角形$\triangle \mathrm{AOB}$三个顶点等距的点的坐标是

(A) \( (x

已知

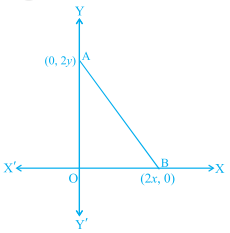
三角形$\triangle \mathrm{AOB}$的三个顶点是 $0(0, 0), A(0,2y)$ 和 $B(2x, 0)$。

要求

我们必须找到与三角形$\triangle \mathrm{AOB}$三个顶点等距的点的坐标。

解答

设与三个顶点$0(0,0)$, $A(0,2 y)$ 和 $B(2 x, 0)$ 等距的点的坐标为 $P(h, k)$。

这意味着，

$P O=P A=P B$

平方后，我们得到，

$(P O)^{2}=(P A)^{2}=(P B)^{2}$

使用距离公式

$[\sqrt{(h-0)^{2}+(k-0)^{2}}]^{2} }=[\sqrt{(h-0)^{2}+(k-2 y)^{2}}]^{2}=[\sqrt{(h-2 x)^{2}+(k-0)^{2}}]^{2}$

$h^{2}+k^{2}=h^{2}+(k-2 y)^{2} =(h-2 x)^{2}+k^{2}$

因此，

$h^{2}+k^{2}=h^{2}+(k-2 y)^{2}$

$k^{2} =k^{2}+4 y^{2}-4 k y$

$4 y(y-k)=0$
$y=k$

$h^{2}+k^{2} =(h-2 x)^{2}+k^{2}$

$h^{2} =h^{2}+4 x^{2}-4 x h$

$4 x(x-h) =0$

$x =h$

所需的点是 $(x, y)$。

Tutorialspoint

更新时间: 2022年10月10日

121 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习