已知:PAST是一个边长为14厘米的正方形,ALS和PLT是半圆。求解:我们需要求阴影部分的面积。解:根据题意,PAST是一个正方形,ALS和PLT是两个半圆。因为PAST是正方形,所以正方形PAST的边长为14厘米。因此PA=AS=ST=TP=14厘米。这里,PT和AS是半圆PLT和ALS的直径。所以半圆PLT和ALS的半径=14/2厘米=7厘米。因此,正方形PAST的面积=(14)²平方厘米=196平方厘米。半圆PLT的面积=22/7×7²/2平方厘米=11×7平方厘米=77平方厘米。半圆ALS的面积=22/7×7²/2平方厘米=11×7平方厘米=77平方厘米。阴影部分的面积=正方形的面积… 阅读更多
已知:一架飞机离开机场,以1000公里/小时的速度向正北飞行。同时,另一架飞机离开同一个机场,以1200公里/小时的速度向正西飞行。求解:我们需要求1.5小时后两架飞机之间的距离。解:第一架飞机的速度=1000公里/小时时间=1.5小时=3/2小时第一架飞机飞行的距离=速度×时间OP=1000×3/2公里=500×3公里=1500公里第一架飞机的最终位置用图中的点P表示。第二架飞机的速度=1200公里/小时时间=1.5小时=3/2小时第二架飞机飞行的距离=速度×时间OQ=1200×3/2公里=600×3公里… 阅读更多
我们无法在粗糙的表面上看到自己的影像,是因为粗糙的表面会产生不规则或随机的反射(光线向各个方向反射)。这也被称为漫反射。
已知:在△ABC中,∠A是钝角,PB⊥AC,QC⊥AB。求证:BC²=(AC×CP+AB×BQ)。证明:在△BPA中,根据勾股定理,AB²=BP²+PA²BP²=AB²-PA²......(i)在△BPC中,根据勾股定理,BC²=BP²+PC²BC²=AB²-PA²+(PA+AC)²BC²=AB²-PA²+PA²+AC²+2PA×ACBC²=AB²+AC²+2PA×AC.....(ii)在△ACQ中,根据勾股定理,AC²=AQ²+QC²QC²=AC²-AQ²......(iii)在△BCQ中,根据勾股定理,BC²=BQ²+QC²BC²=(BA+AQ)²+AC²-AQ²BC²=AB²+AQ²+2AB×AQ+AC²-AQ²BC²=AB²+AC²+2AB×AQ.....(iv)将(ii)和(iv)相加,得到,BC²+BC²=AB²+AC²+2PA×AC+AB²+AC²+2AB×AQ2BC²=2AB²+2AB×AQ+2AC²+2PA×AC2BC²=2AB(AB+AQ)+2AC(AC+PA)两边除以2,得到,BC²=AB×BQ+AC×PC 证毕。阅读更多
已知:在直角三角形ABC中,∠C为直角,D为BC的中点。求证:BC²=4(AD²-AC²)。证明:在△ADC中,根据勾股定理,AD²=AC²+DC²DC²=AD²-AC².....(i)BC=2DC (D为BC的中点)BC²=(2DC)²BC²=4DC²BC²=4(AD²-AC²) (由(i))证毕。
已知:在四边形ABCD中,∠B=90°,AD²=AB²+BC²+CD²。求证:∠ACD=90°。证明:在△ABC中,根据勾股定理,AC²=AB²+BC².....(i)AD²=AB²+BC²+CD²AD²=AC²+CD² (由(i))这说明,根据勾股定理的逆定理,△ACD是一个直角三角形,直角在C。因此,∠ACD=90°证毕。
已知:在下图中,D是BC边的中点,AE⊥BC。BC=a,AC=b,AB=c,ED=x,AD=p,AE=h。求证:c²=p²-ax+a²/4。证明:在△AED中,根据勾股定理,AD²=AE²+ED²AE²=AD²-ED².....(i)在△AEB中,根据勾股定理,AB²=AE²+BE²c²=(AD²-ED²)+(BD-ED)² (由(i)和BE=BD-ED)c²=AD²-ED²+BD²+ED²-2BD×EDc²=AD²+BD²-2BD×EDc²=p²+(a/2)²-2×(a/2)×x (因为DC=BC/2)c²=p²+a²/4-ax证毕。阅读更多
已知:在下图中,D是BC边的中点,AE⊥BC。BC=a,AC=b,AB=c,ED=x,AD=p,AE=h。求证:b²+c²=2p²+a²/2。证明:在△AED中,根据勾股定理,AD²=AE²+ED²AE²=AD²-ED².....(i)在△AEC中,根据勾股定理,AC²=AE²+EC²b²=(AD²-ED²)+(ED+DC)² (由(i))b²=AD²-ED²+ED²+DC²+2ED×DCb²=AD²+DC²+2DC×EDb²=p²+(a/2)²+2×(a/2)×x (因为DC=BC/2)b²=p²+a²/4+ax......(ii)在△AEB中,根据勾股定理,AB²=AE²+BE²c²=(AD²-ED²)+(BD-ED)² (由(i)和BE=BD-ED)c²=AD²-ED²+BD²+ED²-2BD×EDc²=AD²+BD²-2BD×EDc²=p²+(a/2)²-2×(a/2)×x (因为DC=BC/2)c²=p²+a²/4-ax.....(iii)将(ii)和(iii)相加,得到,b²+c²=p²+a²/4+ax+p²+a²/4-axb²+c²=2p²+2×a²/4b²+c²=2p²+a²/2证毕。阅读更多
**已知:**在△ABC中,∠A为钝角,PB⊥AC,QC⊥AB。**求证:** AB×AQ = AC×AP。**证明:**在△APB和△AQC中,∠APB=∠AQC=90°,∠BAP=∠CAQ(对顶角)。因此,△APB∽△AQC(AA相似)。这意味着 AP/AQ = AB/AC(相似三角形的对应边成比例)。⇒ AP×AC = AB×AQ。证毕。
**已知:**在直角三角形ABC中,∠C=90°,D是BC的中点。**求证:**AB²=4AD²-3AC²。**证明:**D是BC的中点。因此,BC=2CD=2BD。在△ABC中,根据勾股定理,AB²=AC²+BC²,AB²=AC²+(2CD)² (BC=2CD),AB²=AC²+4CD²……(i) 在△ACD中,根据勾股定理,AD²=AC²+CD²,CD²=AD²-AC²……(ii) 将(ii)式代入(i)式,得到AB²=AC²+4(AD²-AC²) ,AB²=AC²+4AD²-4AC²,AB²=4AD²-3AC²。证毕。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP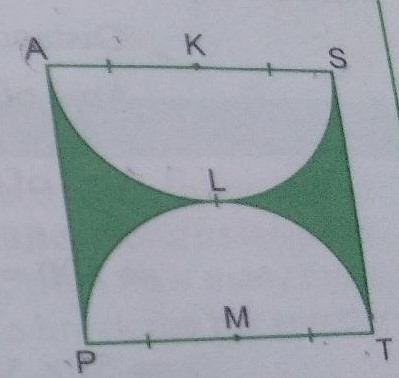 "\
"\
 "\
"\