上下文无关文法的二义性

如果上下文无关文法G对于某个字符串w ∈ L(G)有多个推导树，则称其为二义文法。对于由该文法生成的某个字符串，存在多个最右推导或最左推导。

问题

检查具有以下产生式规则的文法G：

X → X+X | X*X |X| a

是否为二义文法。

解答

让我们找出字符串"a+a*a"的推导树。它有两个最左推导。

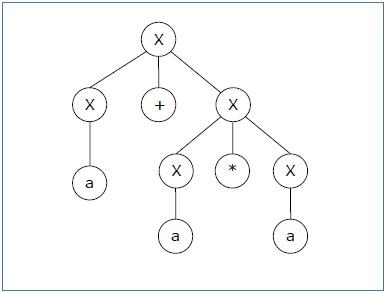
推导1 − X → X+X → a +X → a+ X*X → a+a*X → a+a*a

语法树1 −

推导2 − X → X*X → X+X*X → a+ X*X → a+a*X → a+a*a

语法树2 −

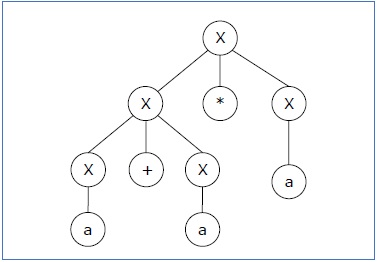
由于对于单个字符串"a+a*a"有两个语法树，因此文法G是二义的。