
- 自动机理论教程
- 自动机理论 - 首页
- 自动机理论 - 入门
- 自动机理论 - 历史
- 自动机理论 - 应用
- 自动机理论术语
- 自动机中字符串的基础知识
- 自动机的集合论
- 语言和文法
- 计算理论中的文法
- 由文法生成的语言
- 乔姆斯基文法分类
- 有限自动机
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NFA)
- 从 NFA 到 DFA 的转换
- DFA 的最小化
- 穆尔机与米利机
- DFA 的补集
- 正则表达式
- 自动机中的正则表达式
- 自动机中的 Arden 定理
- 将正则表达式转换为有限自动机
- 正则文法的泵引理
- 计算理论中的正则集
- 上下文无关文法
- 上下文无关文法 (CFG)
- 上下文无关文法中的二义性
- 上下文无关语言的封闭性
- 简化上下文无关文法
- 乔姆斯基范式 (CNF)
- 格雷巴赫范式 (GNF)
- 上下文无关文法的泵引理
- 下推自动机
- 下推自动机 (PDA)
- 下推自动机的接受
- 从 CFG 构造 PDA
- 下推自动机和解析
- 图灵机
- 图灵机基础 (TM)
- 图灵机接受的语言
- 多磁带图灵机
- 多轨迹图灵机
- 非确定性图灵机
- 半无限带图灵机
- 线性界自动机 (LBA)
- 可计算性和不可判定性
- 图灵语言可判定性
- 不可判定语言
- 图灵机停机问题
- 计算理论中的 Rice 定理
- Post 对应问题 (PCP)
- 自动机理论资源
- 自动机理论 - 快速指南
- 自动机理论 - 资源
- 自动机理论 - 讨论
自动机理论 - 快速指南
自动机理论简介
自动机 - 它是什么?
"自动机"一词源于希腊语 "αὐτόματα",意为"自动"。自动机(复数为自动机)是一种抽象的自动推进计算设备,它自动遵循预定的操作序列。
具有有限状态数的自动机称为有限自动机 (FA) 或有限状态机 (FSM)。
有限自动机的形式化定义
自动机可以用一个 5 元组 (Q, ∑, δ, q0, F) 表示,其中 -
Q 是一个有限的状态集。
∑ 是一个有限的符号集,称为自动机的字母表。
δ 是转移函数。
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
F 是 Q 的一组终态/状态 (F ⊆ Q)。
相关术语
字母表
定义 - 字母表是任何有限的符号集。
示例 - ∑ = {a, b, c, d} 是一个字母表集,其中 'a'、'b'、'c' 和 'd' 是符号。
字符串
定义 - 字符串是从 ∑ 中取出的符号的有限序列。
示例 - 'cabcad' 是字母表集 ∑ = {a, b, c, d} 上的一个有效字符串
字符串的长度
定义 - 字符串中存在的符号数。(用|S|表示)。
示例 -
如果 S = 'cabcad',|S|= 6
如果 |S|= 0,则称为空字符串(用λ或ε表示)
克莱尼星号
定义 - 克莱尼星号∑*是符号或字符串集∑上的一个一元运算符,它给出∑上所有可能长度的所有可能字符串的无限集,包括λ。
表示 - ∑* = ∑0 ∪ ∑1 ∪ ∑2 ∪……. 其中 ∑p 是长度为 p 的所有可能字符串的集合。
示例 - 如果 ∑ = {a, b},∑* = {λ, a, b, aa, ab, ba, bb,………..}
克莱尼闭包/加号
定义 - 集合∑+是∑上所有可能长度的所有可能字符串的无限集,不包括λ。
表示 - ∑+ = ∑1 ∪ ∑2 ∪ ∑3 ∪…….
∑+ = ∑* − { λ }
示例 - 如果 ∑ = { a, b } ,∑+ = { a, b, aa, ab, ba, bb,………..}
语言
定义 - 语言是某个字母表 ∑ 的 ∑* 的子集。它可以是有限的或无限的。
示例 - 如果语言取 ∑ = {a, b} 上长度为 2 的所有可能字符串,则 L = { ab, aa, ba, bb }
确定性有限自动机
有限自动机可以分为两种类型 -
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NDFA / NFA)
确定性有限自动机 (DFA)
在 DFA 中,对于每个输入符号,都可以确定机器将移动到的状态。因此,它被称为确定性自动机。由于它具有有限数量的状态,因此该机器称为确定性有限机或确定性有限自动机。
DFA 的形式化定义
DFA 可以用一个 5 元组 (Q, ∑, δ, q0, F) 表示,其中 -
Q 是一个有限的状态集。
∑ 是一个有限的符号集,称为字母表。
δ 是转移函数,其中 δ: Q × ∑ → Q
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
F 是 Q 的一组终态/状态 (F ⊆ Q)。
DFA 的图形表示
DFA 用称为状态图的有向图表示。
- 顶点表示状态。
- 用输入字母表标记的弧表示转移。
- 初始状态用一个空入射弧表示。
- 终态用双圆表示。
示例
令一个确定性有限自动机为 →
- Q = {a, b, c},
- ∑ = {0, 1},
- q0 = {a},
- F = {c}, 以及
转移函数 δ 如以下表格所示 -
| 当前状态 | 输入 0 的下一状态 | 输入 1 的下一状态 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
它的图形表示如下所示 -
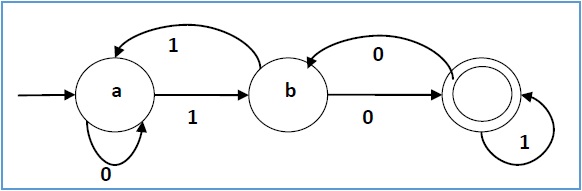
非确定性有限自动机
在 NDFA 中,对于特定的输入符号,机器可以移动到机器中任何状态的组合。换句话说,无法确定机器移动到的确切状态。因此,它被称为非确定性自动机。由于它具有有限数量的状态,因此该机器称为非确定性有限机或非确定性有限自动机。
NDFA 的形式化定义
NDFA 可以用一个 5 元组 (Q, ∑, δ, q0, F) 表示,其中 -
Q 是一个有限的状态集。
∑ 是一个有限的符号集,称为字母表。
δ 是转移函数,其中 δ: Q × ∑ → 2Q
(这里取了 Q 的幂集 (2Q),因为在 NDFA 的情况下,从一个状态可以转移到 Q 状态的任何组合)
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
F 是 Q 的一组终态/状态 (F ⊆ Q)。
NDFA 的图形表示:(与 DFA 相同)
NDFA 用称为状态图的有向图表示。
- 顶点表示状态。
- 用输入字母表标记的弧表示转移。
- 初始状态用一个空入射弧表示。
- 终态用双圆表示。
示例
令一个非确定性有限自动机为 →
- Q = {a, b, c}
- ∑ = {0, 1}
- q0 = {a}
- F = {c}
转移函数 δ 如下所示 -
| 当前状态 | 输入 0 的下一状态 | 输入 1 的下一状态 |
|---|---|---|
| a | a, b | b |
| b | c | a, c |
| c | b, c | c |
它的图形表示如下所示 -
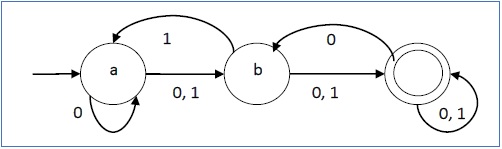
DFA 与 NDFA 的比较
下表列出了 DFA 和 NDFA 之间的区别。
| DFA | NDFA |
|---|---|
| 对于每个输入符号,从一个状态到单个特定下一状态的转换。因此,它被称为确定性的。 | 对于每个输入符号,从一个状态到多个下一状态的转换。因此,它被称为非确定性的。 |
| DFA 中没有看到空字符串转换。 | NDFA 允许空字符串转换。 |
| DFA 中允许回溯 | 在 NDFA 中,回溯并不总是可能的。 |
| 需要更多空间。 | 需要更少的空间。 |
| 如果一个字符串转换到终态,则它被 DFA 接受。 | 如果所有可能的转换中至少有一个以终态结束,则一个字符串被 NDFA 接受。 |
接受器、分类器和转换器
接受器(识别器)
计算布尔函数的自动机称为接受器。接受器的所有状态要么接受,要么拒绝给它的输入。
分类器
分类器具有两个以上终态,并在终止时给出单个输出。
转换器
根据当前输入和/或先前状态产生输出的自动机称为转换器。转换器可以分为两种类型 -
米利机 - 输出取决于当前状态和当前输入。
穆尔机 - 输出仅取决于当前状态。
DFA 和 NDFA 的可接受性
当且仅当 DFA/NDFA 从初始状态开始,在完全读取字符串后结束于接受状态(任何终态)时,字符串被 DFA/NDFA 接受。
字符串 S 被 DFA/NDFA (Q, ∑, δ, q0, F) 接受,当且仅当
δ*(q0, S) ∈ F
DFA/NDFA 接受的语言L为
{S | S ∈ ∑* 且 δ*(q0, S) ∈ F}
字符串 S′ 未被 DFA/NDFA (Q, ∑, δ, q0, F) 接受,当且仅当
δ*(q0, S′) ∉ F
DFA/NDFA 未接受的语言 L′(接受语言 L 的补集)为
{S | S ∈ ∑* 且 δ*(q0, S) ∉ F}
示例
让我们考虑图 1.3 中所示的 DFA。从 DFA 可以推导出可接受的字符串。
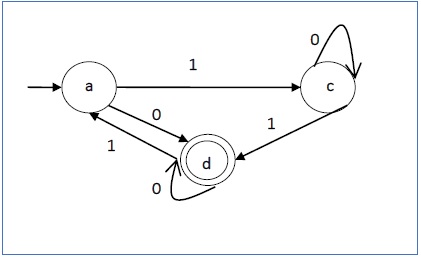
上述 DFA 接受的字符串:{0, 00, 11, 010, 101, ...........}
上述 DFA 未接受的字符串:{1, 011, 111, ........}
NDFA 到 DFA 的转换
问题陈述
令X = (Qx, ∑, δx, q0, Fx)为一个接受语言 L(X) 的 NDFA。我们必须设计一个等价的 DFA Y = (Qy, ∑, δy, q0, Fy),使得L(Y) = L(X)。以下过程将 NDFA 转换为其等价的 DFA -
算法
输入 - 一个 NDFA
输出 - 一个等价的 DFA
步骤 1 - 从给定的 NDFA 创建状态表。
步骤 2 - 在等价 DFA 的可能输入字母表下创建一个空白状态表。
步骤 3 - 将 DFA 的起始状态标记为 q0(与 NDFA 相同)。
步骤 4 - 找到每个可能输入字母表的状态组合 {Q0, Q1,... , Qn}。
步骤 5 - 每次我们在输入字母表列下生成一个新的 DFA 状态时,我们都必须再次应用步骤 4,否则转到步骤 6。
步骤 6 - 包含 NDFA 的任何终态的状态是等价 DFA 的终态。
示例
让我们考虑下图所示的 NDFA。
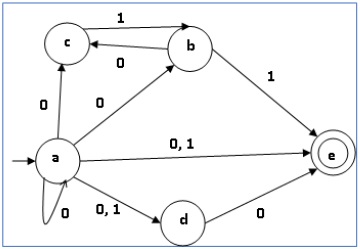
| q | δ(q,0) | δ(q,1) |
|---|---|---|
| a | {a,b,c,d,e} | {d,e} |
| b | {c} | {e} |
| c | ∅ | {b} |
| d | {e} | ∅ |
| e | ∅ | ∅ |
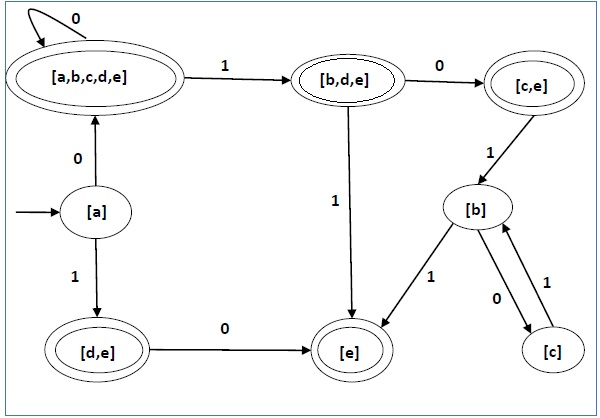
使用上述算法,我们可以找到其等价的DFA。DFA的状态表如下所示。
| q | δ(q,0) | δ(q,1) |
|---|---|---|
| [a] | [a,b,c,d,e] | [d,e] |
| [a,b,c,d,e] | [a,b,c,d,e] | [b,d,e] |
| [d,e] | [e] | ∅ |
| [b,d,e] | [c,e] | [e] |
| [e] | ∅ | ∅ |
| [c, e] | ∅ | [b] |
| [b] | [c] | [e] |
| [c] | ∅ | [b] |
DFA的状态图如下所示:
DFA最小化
使用Myhill-Nerode定理进行DFA最小化
算法
输入 - DFA
输出 - 最小化的DFA
步骤1 - 为所有状态对(Qi, Qj)(不一定直接连接)绘制表格 [最初所有均未标记]
步骤2 - 考虑DFA中每个状态对(Qi, Qj),其中Qi ∈ F且Qj ∉ F,反之亦然,并标记它们。[这里F是终结状态集]
步骤3 - 重复此步骤,直到我们无法再标记任何状态 -
如果存在未标记的对(Qi, Qj),则在对于某些输入字母,对{δ (Qi, A), δ (Qi, A)}被标记时标记它。
步骤4 - 组合所有未标记的对(Qi, Qj),并在简化的DFA中将其设为单个状态。
示例
让我们使用算法2来最小化下面显示的DFA。

步骤1 - 我们为所有状态对绘制表格。
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| f |
步骤2 - 我们标记状态对。
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ |
步骤3 - 我们将尝试传递地标记状态对,用绿色复选标记表示。如果我们将1输入到状态“a”和“f”,它将分别转到状态“c”和“f”。(c, f)已被标记,因此我们将标记对(a, f)。现在,我们将1输入到状态“b”和“f”;它将分别转到状态“d”和“f”。(d, f)已被标记,因此我们将标记对(b, f)。
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ | ✔ | ✔ |
步骤3之后,我们得到了未标记的状态组合{a, b} {c, d} {c, e} {d, e}。
我们可以将{c, d} {c, e} {d, e}重新组合成{c, d, e}
因此,我们得到了两个组合状态:{a, b}和{c, d, e}
所以最终最小化的DFA将包含三个状态{f}、{a, b}和{c, d, e}
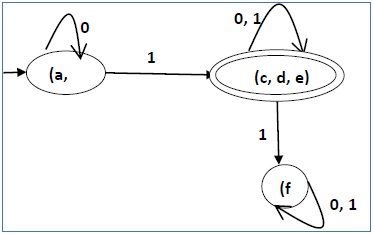
使用等价定理进行DFA最小化
如果X和Y是DFA中的两个状态,如果它们不可区分,则可以将这两个状态组合成{X, Y}。如果至少存在一个字符串S,使得δ (X, S)和δ (Y, S)中一个为接受状态而另一个为非接受状态,则这两个状态是可区分的。因此,当且仅当所有状态都可区分时,DFA才是最小的。
算法3
步骤1 - 所有状态Q被分成两个分区 - 终结状态和非终结状态,并表示为P0。分区中的所有状态都是0阶等价的。取一个计数器k并将其初始化为0。
步骤2 - 将k加1。对于Pk中的每个分区,如果Pk中的状态是k可区分的,则将它们分成两个分区。如果存在一个输入S,使得δ(X, S)和δ(Y, S)是(k-1)可区分的,则此分区中的两个状态X和Y是k可区分的。
步骤3 - 如果Pk ≠ Pk-1,则重复步骤2,否则转到步骤4。
步骤4 - 组合k阶等价集,并将它们设为简化DFA的新状态。
示例
让我们考虑以下DFA:
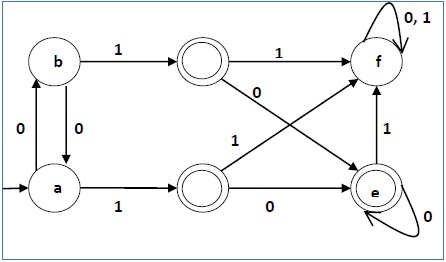
| q | δ(q,0) | δ(q,1) |
|---|---|---|
| a | b | c |
| b | a | d |
| c | e | f |
| d | e | f |
| e | e | f |
| f | f | f |
让我们将上述算法应用于上述DFA:
- P0 = {(c,d,e), (a,b,f)}
- P1 = {(c,d,e), (a,b),(f)}
- P2 = {(c,d,e), (a,b),(f)}
因此,P1 = P2。
简化DFA中有三个状态。简化DFA如下:
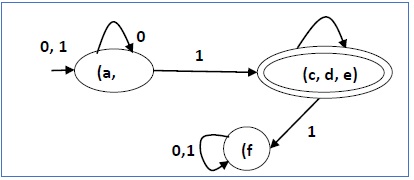
| Q | δ(q,0) | δ(q,1) |
|---|---|---|
| (a, b) | (a, b) | (c,d,e) |
| (c,d,e) | (c,d,e) | (f) |
| (f) | (f) | (f) |
Moore和Mealy机
有限自动机可能对每个转换都有输出。有两种类型的有限状态机生成输出:
- Mealy机
- Moore机
Mealy机
Mealy机是一种FSM,其输出取决于当前状态以及当前输入。
它可以用一个6元组(Q, ∑, O, δ, X, q0)来描述,其中:
Q 是一个有限的状态集。
∑是一组有限的符号,称为输入字母表。
O是一组有限的符号,称为输出字母表。
δ是输入转移函数,其中δ: Q × ∑ → Q
X是输出转移函数,其中X: Q × ∑ → O
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
Mealy机的状态表如下所示:
| 当前状态 | 下一个状态 | |||
|---|---|---|---|---|
| 输入 = 0 | 输入 = 1 | |||
| 状态 | 输出 | 状态 | 输出 | |
| → a | b | x1 | c | x1 |
| b | b | x2 | d | x3 |
| c | d | x3 | c | x1 |
| d | d | x3 | d | x2 |
上述Mealy机的状态图如下:
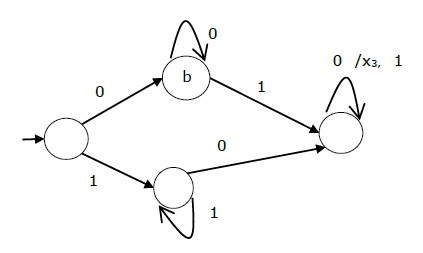
Moore机
Moore机是一种FSM,其输出仅取决于当前状态。
Moore机可以用一个6元组(Q, ∑, O, δ, X, q0)来描述,其中:
Q 是一个有限的状态集。
∑是一组有限的符号,称为输入字母表。
O是一组有限的符号,称为输出字母表。
δ是输入转移函数,其中δ: Q × ∑ → Q
X是输出转移函数,其中X: Q → O
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
Moore机的状态表如下所示:
| 当前状态 | 下一个状态 | 输出 | |
|---|---|---|---|
| 输入 = 0 | 输入 = 1 | ||
| → a | b | c | x2 |
| b | b | d | x1 |
| c | c | d | x2 |
| d | d | d | x3 |
上述Moore机的状态图如下:
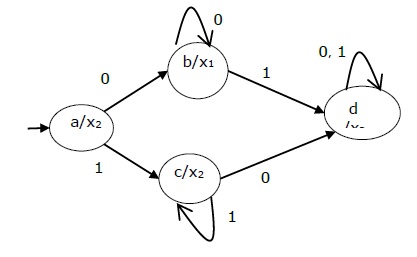
Mealy机与Moore机
下表突出显示了区分Mealy机与Moore机的要点。
| Mealy机 | Moore机 |
|---|---|
| 输出同时取决于当前状态和当前输入 | 输出仅取决于当前状态。 |
| 通常,它比Moore机具有更少的态。 | 通常,它比Mealy机具有更多的态。 |
| 输出函数的值是转换的函数,以及在当前状态上执行输入逻辑时发生的更改。 | 输出函数的值是当前状态的函数,以及每次状态发生变化时在时钟沿发生的更改。 |
| Mealy机对输入的反应更快。它们通常在同一个时钟周期内做出反应。 | 在Moore机中,需要更多的逻辑来解码输出,从而导致更多的电路延迟。它们通常在下一个时钟周期做出反应。 |
Moore机转换为Mealy机
算法4
输入 - Moore机
输出 - Mealy机
步骤1 - 获取一个空白的Mealy机转换表格式。
步骤2 - 将所有Moore机转换状态复制到此表格式中。
步骤3 - 检查Moore机状态表中的当前状态及其相应的输出;如果对于状态Qi输出为m,则将其复制到Mealy机状态表的输出列中,无论Qi出现在下一个状态的何处。
示例
让我们考虑以下Moore机:
| 当前状态 | 下一个状态 | 输出 | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b | 1 |
| b | a | d | 0 |
| c | c | c | 0 |
| d | b | a | 1 |
现在我们应用算法4将其转换为Mealy机。
步骤1和2 -
| 当前状态 | 下一个状态 | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| 状态 | 输出 | 状态 | 输出 | |
| → a | d | b | ||
| b | a | d | ||
| c | c | c | ||
| d | b | a | ||
步骤3 -
| 当前状态 | 下一个状态 | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| 状态 | 输出 | 状态 | 输出 | |
| => a | d | 1 | b | 0 |
| b | a | 1 | d | 1 |
| c | c | 0 | c | 0 |
| d | b | 0 | a | 1 |
Mealy机转换为Moore机
算法5
输入 - Mealy机
输出 - Moore机
步骤1 - 计算Mealy机状态表中每个状态(Qi)的不同的输出数量。
步骤2 - 如果Qi的所有输出都相同,则复制状态Qi。如果它有n个不同的输出,则将Qi分解成n个状态作为Qin,其中n = 0, 1, 2.......
步骤3 - 如果初始状态的输出为1,则在开头插入一个新的初始状态,该状态输出0。
示例
让我们考虑以下Mealy机:
| 当前状态 | 下一个状态 | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| 下一个状态 | 输出 | 下一个状态 | 输出 | |
| → a | d | 0 | b | 1 |
| b | a | 1 | d | 0 |
| c | c | 1 | c | 0 |
| d | b | 0 | a | 1 |
这里,状态“a”和“d”分别仅输出1和0,因此我们保留状态“a”和“d”。但是状态“b”和“c”产生不同的输出(1和0)。因此,我们将b分成b0, b1,并将c分成c0, c1。
| 当前状态 | 下一个状态 | 输出 | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b1 | 1 |
| b0 | a | d | 0 |
| b1 | a | d | 1 |
| c0 | c1 | C0 | 0 |
| c1 | c1 | C0 | 1 |
| d | b0 | a | 0 |
语法简介
从文学意义上讲,语法表示自然语言对话的句法规则。自英语、梵语、普通话等自然语言诞生以来,语言学家就试图定义语法。
形式语言理论在计算机科学领域得到了广泛的应用。Noam Chomsky在1956年提出了一个数学语法模型,该模型可用于编写计算机语言。
语法
语法G可以正式地写成一个4元组(N, T, S, P),其中:
N或VN是一组变量或非终结符。
T或∑是一组终结符。
S是一个称为起始符的特殊变量,S ∈ N
P是终结符和非终结符的产生式规则。产生式规则的形式为α → β,其中α和β是VN ∪ ∑上的字符串,并且α至少有一个符号属于VN。
示例
语法G1 -
({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
这里,
S、A和B是非终结符;
a和b是终结符
S是起始符,S ∈ N
产生式P : S → AB, A → a, B → b
示例
语法G2 -
(({S, A}, {a, b}, S,{S → aAb, aA → aaAb, A → ε } )
这里,
S和A是非终结符。
a和b是终结符。
ε是空字符串。
S是起始符,S ∈ N
产生式P : S → aAb, aA → aaAb, A → ε
来自语法的推导
可以使用语法中的产生式从其他字符串推导出字符串。如果语法G有一个产生式α → β,我们可以说x α y在G中推导出x β y。此推导写为:
x α y ⇒G x β y
示例
让我们考虑以下语法:
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε } )
可以推导出的某些字符串为:
S ⇒ aAb 使用产生式S → aAb
⇒ aaAbb 使用产生式aA → aAb
⇒ aaaAbbb 使用产生式aA → aaAb
⇒ aaabbb 使用产生式A → ε
由文法生成的语言
可以从语法中推导出的所有字符串的集合称为从该语法中生成的语言。由语法G生成的语言是正式定义的子集
L(G)={W|W ∈ ∑*, S ⇒G W}
如果L(G1) = L(G2),则语法G1等价于语法G2。
示例
如果存在一个语法
G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}
这里S产生AB,我们可以用a替换A,用b替换B。这里,唯一被接受的字符串是ab,即
L(G) = {ab}
示例
假设我们有以下语法:
G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA|a, B → bB|b}
这个语法生成的语言:
L(G) = {ab, a2b, ab2, a2b2, ………}
= {am bn | m ≥ 1 且 n ≥ 1}
生成语言的语法的构造
我们将考虑一些语言,并将其转换为产生这些语言的语法G。
示例
问题 - 假设,L (G) = {am bn | m ≥ 0 且 n > 0}。我们必须找出产生L(G)的语法G。
解答
由于L(G) = {am bn | m ≥ 0 且 n > 0}
被接受的字符串集可以改写为:
L(G) = {b, ab,bb, aab, abb, …….}
这里,起始符号必须至少包含一个'b',前面可以有任意数量的'a',包括空。
为了接受字符串集{b, ab, bb, aab, abb, …….}, 我们使用了以下产生式:
S → aS , S → B, B → b 和 B → bB
S → B → b (被接受)
S → B → bB → bb (被接受)
S → aS → aB → ab (被接受)
S → aS → aaS → aaB → aab(被接受)
S → aS → aB → abB → abb (被接受)
因此,我们可以证明L(G)中的每个字符串都被产生式集生成的语言所接受。
因此语法:
G: ({S, A, B}, {a, b}, S, { S → aS | B , B → b | bB })
示例
问题 - 假设,L (G) = {am bn | m > 0 且 n ≥ 0}。我们必须找出产生L(G)的语法G。
解答 -
由于L(G) = {am bn | m > 0 且 n ≥ 0},被接受的字符串集可以改写为:
L(G) = {a, aa, ab, aaa, aab ,abb, …….}
这里,起始符号必须至少包含一个'a',后面可以有任意数量的'b',包括空。
为了接受字符串集{a, aa, ab, aaa, aab, abb, …….}, 我们使用了以下产生式:
S → aA, A → aA , A → B, B → bB ,B → λ
S → aA → aB → aλ → a (被接受)
S → aA → aaA → aaB → aaλ → aa (被接受)
S → aA → aB → abB → abλ → ab (被接受)
S → aA → aaA → aaaA → aaaB → aaaλ → aaa (被接受)
S → aA → aaA → aaB → aabB → aabλ → aab (被接受)
S → aA → aB → abB → abbB → abbλ → abb (被接受)
因此,我们可以证明L(G)中的每个字符串都被产生式集生成的语言所接受。
因此语法:
G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB })
乔姆斯基文法分类
根据诺姆·乔姆斯基,有四种类型的语法:0型、1型、2型和3型。下表显示了它们之间的区别:
| 语法类型 | 接受的语法 | 接受的语言 | 自动机 |
|---|---|---|---|
| 0型 | 无限制语法 | 递归可枚举语言 | 图灵机 |
| 1型 | 上下文敏感语法 | 上下文敏感语言 | 线性有界自动机 |
| 2型 | 上下文无关语法 | 上下文无关语言 | 下推自动机 |
| 3型 | 正则语法 | 正则语言 | 有限状态自动机 |
请查看以下插图。它显示了每种语法类型的范围:

3型语法
3型语法生成正则语言。3型语法必须在左侧具有单个非终结符,并且右侧由单个终结符或单个终结符后跟单个非终结符组成。
产生式必须采用以下形式X → a 或 X → aY
其中X, Y ∈ N (非终结符)
且a ∈ T (终结符)
如果S不出现在任何规则的右侧,则允许规则S → ε。
示例
X → ε X → a | aY Y → b
2型语法
2型语法生成上下文无关语言。
产生式必须采用以下形式A → γ
其中 A ∈ N (非终结符)
且γ ∈ (T ∪ N)* (终结符和非终结符的字符串)。
这些语法生成的语言可以被非确定性下推自动机识别。
示例
S → X a X → a X → aX X → abc X → ε
1型语法
1型语法生成上下文敏感语言。产生式必须采用以下形式
α A β → α γ β
其中A ∈ N (非终结符)
且α, β, γ ∈ (T ∪ N)* (终结符和非终结符的字符串)
字符串α和β可以为空,但γ不能为空。
如果S不出现在任何规则的右侧,则允许规则S → ε。这些语法生成的语言可以被线性有界自动机识别。
示例
AB → AbBc A → bcA B → b
0型语法
0型语法生成递归可枚举语言。产生式没有限制。它们是任何短语结构语法,包括所有形式语法。
它们生成由图灵机识别的语言。
产生式可以采用α → β的形式,其中α是终结符和非终结符的字符串,至少包含一个非终结符,并且α不能为null。β是终结符和非终结符的字符串。
示例
S → ACaB Bc → acB CB → DB aD → Db
正则表达式
正则表达式可以递归定义如下:
ε是一个正则表达式,表示包含空字符串的语言。(L (ε) = {ε})
φ是一个正则表达式,表示空语言。(L (φ) = { })
x是一个正则表达式,其中L = {x}
如果X是一个表示语言L(X)的正则表达式,并且Y是一个表示语言L(Y)的正则表达式,则
X + Y是一个对应于语言L(X) ∪ L(Y)的正则表达式,其中L(X+Y) = L(X) ∪ L(Y)。
X . Y是一个对应于语言L(X) . L(Y)的正则表达式,其中L(X.Y) = L(X) . L(Y)
R*是一个对应于语言L(R*)的正则表达式,其中L(R*) = (L(R))*
如果我们从1到5多次应用任何规则,它们都是正则表达式。
一些RE示例
| 正则表达式 | 正则集 |
|---|---|
| (0 + 10*) | L = { 0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | L = {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | L = {ε, 0, 1, 01} |
| (a+b)* | 任意长度的a和b的字符串集,包括空字符串。因此L = { ε, a, b, aa , ab , bb , ba, aaa…….} |
| (a+b)*abb | 以字符串abb结尾的a和b的字符串集。因此L = {abb, aabb, babb, aaabb, ababb, …………..} |
| (11)* | 包含偶数个1的集合,包括空字符串,因此L= {ε, 11, 1111, 111111, ……….} |
| (aa)*(bb)*b | 包含偶数个a后跟奇数个b的字符串集,因此L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..} |
| (aa + ab + ba + bb)* | 偶数长度的a和b的字符串可以通过连接aa、ab、ba和bb的任意组合(包括空)来获得,因此L = {aa, ab, ba, bb, aaab, aaba, …………..} |
正则集
任何表示正则表达式值的集合都称为正则集。
正则集的性质
性质1. 两个正则集的并集是正则的。
证明 -
让我们取两个正则表达式
RE1 = a(aa)* 和 RE2 = (aa)*
因此,L1 = {a, aaa, aaaaa,.....}(奇数长度的字符串,不包括空)
且L2 ={ ε, aa, aaaa, aaaaaa,.......}(偶数长度的字符串,包括空)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(所有可能长度的字符串,包括空)
RE (L1 ∪ L2) = a* (它本身就是一个正则表达式)
因此,得证。
性质2. 两个正则集的交集是正则的。
证明 -
让我们取两个正则表达式
RE1 = a(a*) 和 RE2 = (aa)*
因此,L1 = { a,aa, aaa, aaaa, ....}(所有可能长度的字符串,不包括空)
L2 = { ε, aa, aaaa, aaaaaa,.......}(偶数长度的字符串,包括空)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......}(偶数长度的字符串,不包括空)
RE (L1 ∩ L2) = aa(aa)*,它本身就是一个正则表达式。
因此,得证。
性质3. 正则集的补集是正则的。
证明 -
让我们取一个正则表达式:
RE = (aa)*
因此,L = {ε, aa, aaaa, aaaaaa, .......}(偶数长度的字符串,包括空)
L的补集是不在L中的所有字符串。
因此,L’ = {a, aaa, aaaaa, .....}(奇数长度的字符串,不包括空)
RE (L’) = a(aa)*,它本身就是一个正则表达式。
因此,得证。
性质4. 两个正则集的差集是正则的。
证明 -
让我们取两个正则表达式:
RE1 = a (a*) 和 RE2 = (aa)*
因此,L1 = {a, aa, aaa, aaaa, ....}(所有可能长度的字符串,不包括空)
L2 = { ε, aa, aaaa, aaaaaa,.......}(偶数长度的字符串,包括空)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(所有奇数长度的字符串,不包括空)
RE (L1 – L2) = a (aa)*,它是一个正则表达式。
因此,得证。
性质5. 正则集的反转是正则的。
证明 -
我们必须证明如果L是一个正则集,则LR也是正则的。
令,L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10,它是正则的
因此,得证。
性质6. 正则集的闭包是正则的。
证明 -
如果L = {a, aaa, aaaaa, .......} (奇数长度的字符串,不包括空)
即, RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (所有长度的字符串,不包括空)
RE (L*) = a (a)*
因此,得证。
性质7. 两个正则集的连接是正则的。
证明 -
令 RE1 = (0+1)*0 和 RE2 = 01(0+1)*
这里, L1 = {0, 00, 10, 000, 010, ......} (以0结尾的字符串集合)
并且 L2 = {01, 010,011,.....} (以01开头的字符串集合)
那么, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
包含001作为子串的字符串集合,可以用正则表达式表示为 -(0 + 1)*001(0 + 1)*
因此,得证。
正则表达式的恒等式
给定R、P、L、Q为正则表达式,以下恒等式成立:
- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (并集的恒等式)
- R ε = ε R = R (连接的恒等式)
- ∅ L = L ∅ = ∅ (连接的零元)
- R + R = R (幂等律)
- L (M + N) = LM + LN (左分配律)
- (M + N) L = ML + NL (右分配律)
- ε + RR* = ε + R*R = R*
Arden定理
为了找出有限自动机的正则表达式,我们使用Arden定理以及正则表达式的性质。
陈述 −
设P和Q为两个正则表达式。
如果P不包含空字符串,则R = Q + RP有一个唯一的解,即R = QP*
证明 -
R = Q + (Q + RP)P [代入R = Q + RP的值]
= Q + QP + RPP
当我们反复递归地代入R的值时,得到以下等式:
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [因为P*表示(ε + P + P2 + P3 + ….) ]
因此,得证。
应用Arden定理的假设
- 状态转换图不能有空转移
- 它必须只有一个初始状态
方法
步骤1 − 为具有n个状态和初始状态q1的DFA的所有状态创建如下形式的方程。
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
…………………………
…………………………
…………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij表示从qi到qj的边的标签集,如果没有这样的边存在,则Rij = ∅
步骤2 − 求解这些方程以获得最终状态关于Rij的方程
问题
构造一个与下面给定的自动机对应的正则表达式:
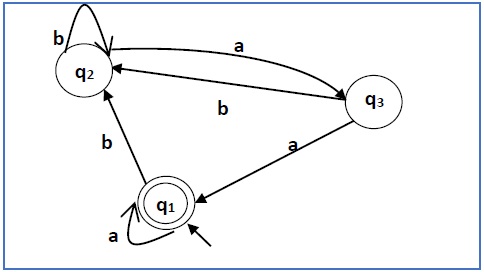
解答 −
这里初始状态和最终状态是q1。
三个状态q1、q2和q3的方程如下:
q1 = q1a + q3a + ε (ε转移是因为q1是初始状态)
q2 = q1b + q2b + q3b
q3 = q2a
现在,我们将求解这三个方程:
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (代入q3的值)
= q1b + q2(b + ab)
= q1b (b + ab)* (应用Arden定理)
q1 = q1a + q3a + ε
= q1a + q2aa + ε (代入q3的值)
= q1a + q1b(b + ab*)aa + ε (代入q2的值)
= q1(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
因此,正则表达式为(a + b(b + ab)*aa)*。
问题
构造一个与下面给定的自动机对应的正则表达式:
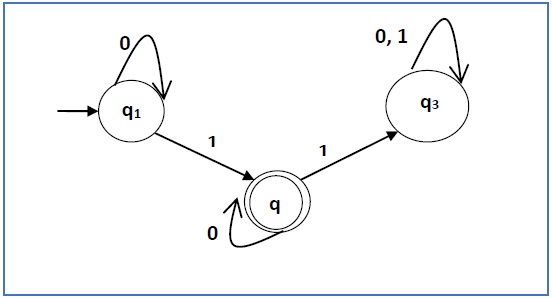
解答 −
这里初始状态是q1,最终状态是q2
现在我们写下方程:
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
现在,我们将求解这三个方程:
q1 = ε0* [因为,εR = R]
所以,q1 = 0*
q2 = 0*1 + q20
所以,q2 = 0*1(0)* [根据Arden定理]
因此,正则表达式为0*10*。
从RE构造FA
我们可以使用Thompson构造法从正则表达式中找出有限自动机。我们将正则表达式简化为最小的正则表达式,并将这些表达式转换为NFA,最后转换为DFA。
一些基本的RA表达式如下:
情况1 − 对于正则表达式“a”,我们可以构造以下FA:
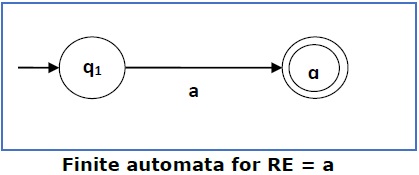
情况2 − 对于正则表达式“ab”,我们可以构造以下FA:
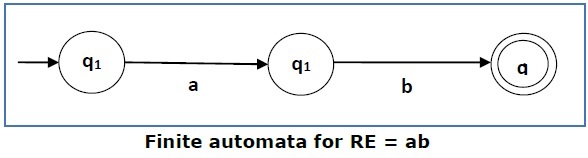
情况3 − 对于正则表达式(a+b),我们可以构造以下FA:
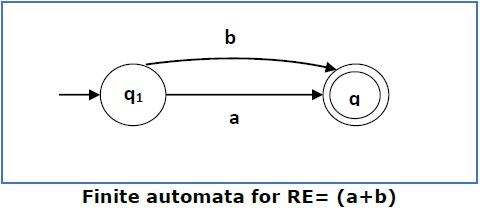
情况4 − 对于正则表达式(a+b)*,我们可以构造以下FA:
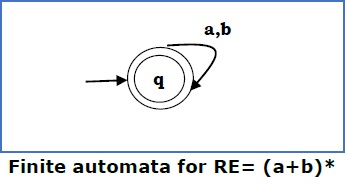
方法
步骤1 从给定的正则表达式构造一个带空转移的NFA。
步骤2 从NFA中移除空转移,并将其转换为等价的DFA。
问题
将以下RA转换为其等价的DFA:1 (0 + 1)* 0
解答
我们将连接三个表达式“1”、“(0 + 1)*”和“0”
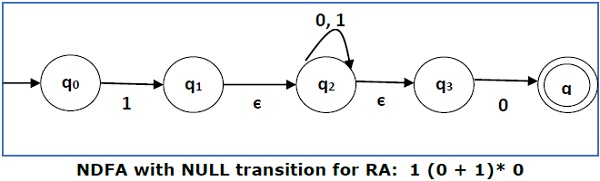
现在我们将移除ε转移。在从NDFA中移除ε转移后,我们得到以下结果:
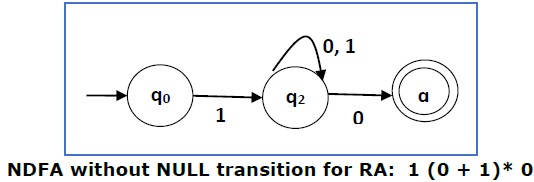
这是一个与RE:1 (0 + 1)* 0对应的NDFA。如果你想将其转换为DFA,只需应用第1章中讨论的将NDFA转换为DFA的方法。
带空转移的有限自动机 (NFA-ε)
带空转移的有限自动机(FA-ε)不仅在给出字母集的输入后进行转移,而且在没有任何输入符号的情况下进行转移。这种无输入的转移称为空转移。
NFA-ε用一个5元组(Q, ∑, δ, q0, F)正式表示,它由以下部分组成
Q − 一组有限的状态
∑ − 一组有限的输入符号
δ − 一个转移函数δ : Q × (∑ ∪ {ε}) → 2Q
q0 − 一个初始状态q0 ∈ Q
F − 一组最终状态/状态Q (F⊆Q)。
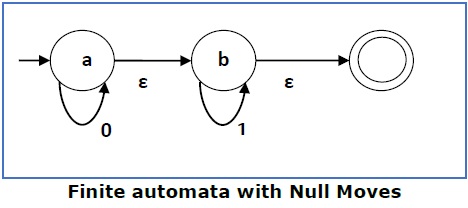
上述(FA-ε)接受一个字符串集:{0, 1, 01}
从有限自动机中移除空转移
如果在一个NDFA中,在顶点X到顶点Y之间存在ϵ-转移,我们可以使用以下步骤将其移除:
- 找到从Y出发的所有外向边。
- 复制所有这些从X开始的边,而不更改边标签。
- 如果X是初始状态,则使Y也成为初始状态。
- 如果Y是最终状态,则使X也成为最终状态。
问题
将以下NFA-ε转换为没有空转移的NFA。
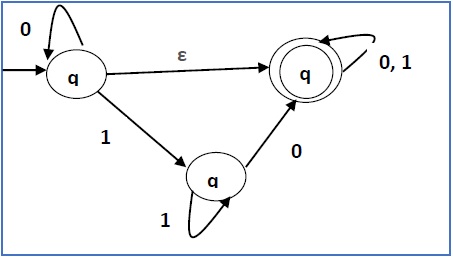
解答
步骤1 −
这里ε转移在q1和q2之间,所以设q1为X,qf为Y。
这里从qf出发的外向边是对于输入0和1到qf。
步骤2 −
现在我们将复制所有这些从q1出发的边,而不更改从qf出发的边,并得到以下FA:
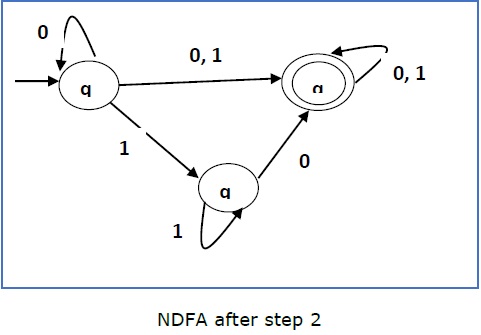
步骤3 -
这里q1是初始状态,所以我们也使qf成为初始状态。
所以FA变为:
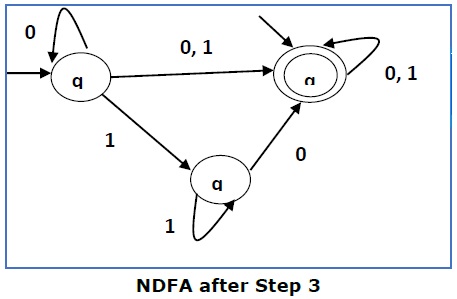
步骤4 −
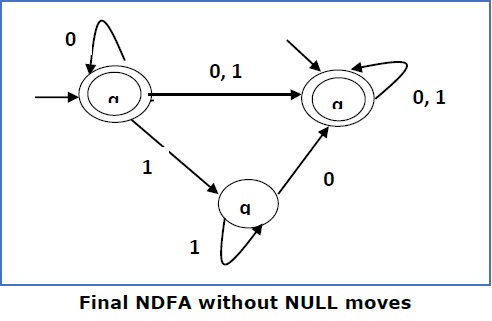
这里qf是最终状态,所以我们也使q1成为最终状态。
所以FA变为:
正则文法的泵引理
定理
设L是一个正则语言。那么存在一个常数‘c’,使得对于L中的每个字符串w:
|w| ≥ c
我们可以将w分解成三个字符串,w = xyz,使得:
- |y| > 0
- |xy| ≤ c
- 对于所有k ≥ 0,字符串xykz也在L中。
泵引理的应用
泵引理用于证明某些语言不是正则语言。它永远不应该用于证明一个语言是正则语言。
如果L是正则的,则它满足泵引理。
如果L不满足泵引理,则它是非正则的。
证明语言L不是正则语言的方法
首先,我们必须假设L是正则的。
所以,泵引理应该对L成立。
使用泵引理得到一个矛盾:
选择w使得|w| ≥ c
选择y使得|y| ≥ 1
选择x使得|xy| ≤ c
将剩余的字符串赋给z.
选择k使得生成的字符串不在L中。
因此L不是正则的。
问题
证明L = {aibi | i ≥ 0}不是正则的。
解答 -
首先,我们假设L是正则的,n是状态数。
设w = anbn。因此|w| = 2n ≥ n。
根据泵引理,设w = xyz,其中|xy| ≤ n。
设x = ap,y = aq,z = arbn,其中p + q + r = n,p ≠ 0,q ≠ 0,r ≠ 0。因此|y| ≠ 0。
设k = 2。则xy2z = apa2qarbn。
a的数量 = (p + 2q + r) = (p + q + r) + q = n + q
因此,xy2z = an+q bn。由于q ≠ 0,xy2z不是anbn的形式。
因此,xy2z不在L中。因此L不是正则的。
DFA补集
如果(Q, ∑, δ, q0, F)是一个接受语言L的DFA,则DFA的补集可以通过交换其接受状态和非接受状态来获得,反之亦然。
我们将以一个例子来阐述这一点:
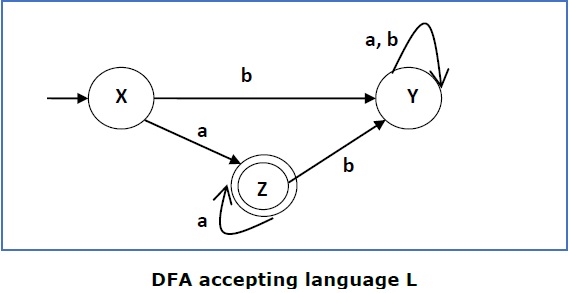
这个DFA接受语言
L = {a, aa, aaa , ............. }
在字母表上
∑ = {a, b}
所以,RE = a+。
现在我们将它的接受状态与它的非接受状态互换,反之亦然,并将得到以下结果:
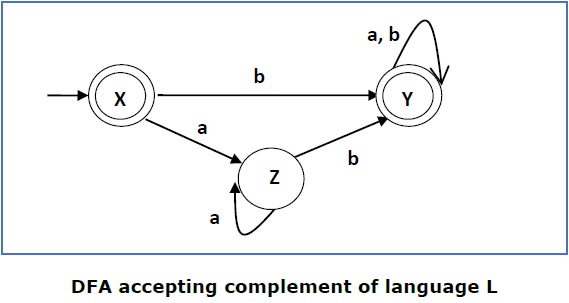
这个DFA接受语言
Ľ = {ε, b, ab ,bb,ba, ............... }
在字母表上
∑ = {a, b}
注意 - 如果我们想对NFA取补集,我们必须先将其转换为DFA,然后像以前的方法一样交换状态。
上下文无关文法简介
定义 - 上下文无关文法(CFG)由一组有限的语法规则组成,是一个四元组(N, T, P, S),其中
N是非终结符的集合。
T是终结符的集合,其中N ∩ T = NULL.
P是一组规则,P: N → (N ∪ T)*,即产生式规则P的左侧没有任何右上下文或左上下文。
S是起始符。
示例
- 文法({A}, {a, b, c}, P, A),P : A → aA, A → abc。
- 文法({S, a, b}, {a, b}, P, S),P: S → aSa, S → bSb, S → ε
- 文法({S, F}, {0, 1}, P, S),P: S → 00S | 11F, F → 00F | ε
推导树的生成
推导树或语法树是一个有序的根树,它以图形方式表示从上下文无关文法推导出的字符串的语义信息。
表示技术
根节点 - 必须用起始符标记。
节点 - 用非终结符标记。
叶子节点 - 用终结符或ε标记。
如果S → x1x2 …… xn是CFG中的一个产生式规则,则语法树/推导树如下:
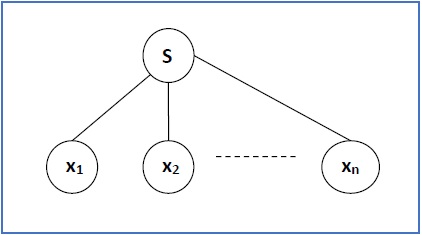
有两种不同的方法来绘制推导树:
自顶向下方法 -
从起始符S开始
使用产生式向下到树的叶子节点
自底向上方法 -
从树的叶子节点开始
向上到根节点,即起始符S
树的推导或结果
语法树的推导或结果是从左到右连接树的叶子节点的标签而获得的最终字符串,忽略空值。但是,如果所有叶子节点都是空值,则推导结果为空值。
示例
设CFG {N,T,P,S}为
N = {S}, T = {a, b}, 起始符 = S, P = S → SS | aSb | ε
从上面CFG的一个推导是“abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb
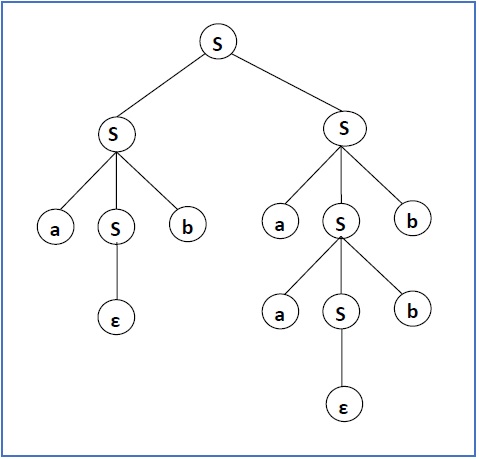
句子形式和部分推导树
部分推导树是推导树/语法树的子树,使得它的所有子节点都在子树中或都不在子树中。
示例
如果在任何CFG中,产生式为:
S → AB, A → aaA | ε, B → Bb| ε
部分推导树可以是以下:
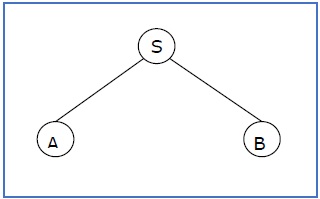
如果部分推导树包含根节点S,则称为句子形式。上面的子树也处于句子形式。
字符串的最左推导和最右推导
最左推导 - 最左推导是通过在每一步都应用最左边的变量的产生式得到的。
最右推导 - 最右推导是通过在每一步都应用最右边的变量的产生式得到的。
示例
设CFG中任意一组产生式规则为
X → X+X | X*X |X| a
在字母表{a}上。
字符串"a+a*a"的最左推导可能是:
X → X+X → a+X → a + X*X → a+a*X → a+a*a
上面字符串的分步推导如下所示:
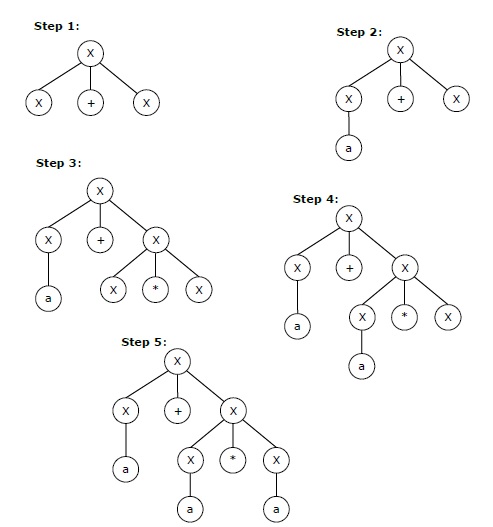
上面字符串"a+a*a"的最右推导可能是:
X → X*X → X*a → X+X*a → X+a*a → a+a*a
上面字符串的分步推导如下所示:
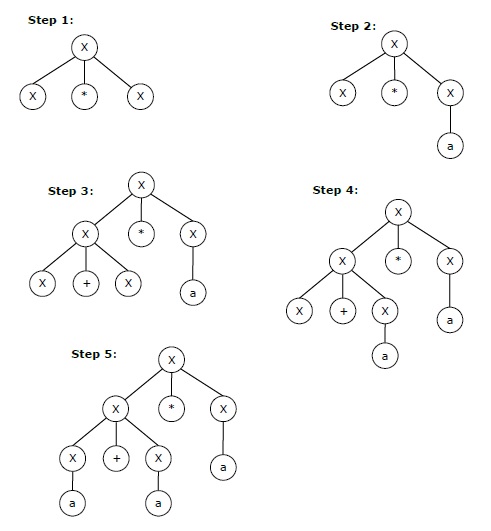
左递归和右递归文法
在上下文无关文法G中,如果存在形式为X → Xa的产生式,其中X是非终结符,‘a’是终结符的字符串,则称为左递归产生式。具有左递归产生式的文法称为左递归文法。
如果在上下文无关文法G中,如果存在形式为X → aX的产生式,其中X是非终结符,‘a’是终结符的字符串,则称为右递归产生式。具有右递归产生式的文法称为右递归文法。
上下文无关文法中的二义性
如果上下文无关文法G对于某个字符串w ∈ L(G)有多个推导树,则称为二义文法。对于从该文法生成的某个字符串,存在多个最右推导或最左推导。
问题
检查具有以下产生式规则的文法G:
X → X+X | X*X |X| a
是否二义的。
解答
让我们找出字符串"a+a*a"的推导树。它有两个最左推导。
推导1 - X → X+X → a +X → a+ X*X → a+a*X → a+a*a
语法树1 -
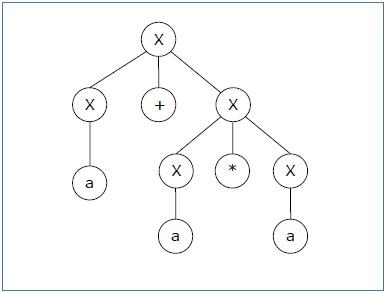
推导2 - X → X*X → X+X*X → a+ X*X → a+a*X → a+a*a
语法树2 -
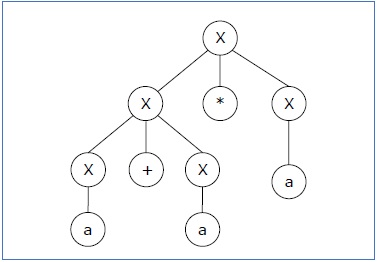
由于单个字符串"a+a*a"有两个语法树,因此文法G是二义的。
CFL闭包性质
上下文无关语言在以下方面是闭合的:
- 并集
- 连接
- Kleene星号运算
并集
设L1和L2是两个上下文无关语言。则L1 ∪ L2也是上下文无关的。
示例
设L1 = { anbn , n > 0}。相应的文法G1将具有P: S1 → aAb|ab
设L2 = { cmdm , m ≥ 0}。相应的文法G2将具有P: S2 → cBb| ε
L1和L2的并集,L = L1 ∪ L2 = { anbn } ∪ { cmdm }
相应的文法G将具有额外的产生式S → S1 | S2
连接
如果L1和L2是上下文无关语言,则L1L2也是上下文无关的。
示例
语言L1和L2的并集,L = L1L2 = { anbncmdm }
相应的文法G将具有额外的产生式S → S1 S2
克莱尼星号
如果L是上下文无关语言,则L*也是上下文无关的。
示例
设L = { anbn , n ≥ 0}。相应的文法G将具有P: S → aAb| ε
Kleene星号L1 = { anbn }*
相应的文法G1将具有额外的产生式S1 → SS1 | ε
上下文无关语言在以下方面不是闭合的:
交集 - 如果L1和L2是上下文无关语言,则L1 ∩ L2不一定上下文无关。
与正则语言的交集 - 如果L1是正则语言,L2是上下文无关语言,则L1 ∩ L2是上下文无关语言。
补集 - 如果L1是上下文无关语言,则L1’可能不是上下文无关的。
CFG简化
在CFG中,可能发生并非所有产生式规则和符号都需要用于字符串的推导。此外,可能存在一些空产生式和单元产生式。消除这些产生式和符号称为CFG的简化。简化基本上包括以下步骤:
- CFG的归约
- 删除单元产生式
- 删除空产生式
CFG的归约
CFG分为两个阶段归约:
阶段1 - 从CFG G导出等价的文法G’,使得每个变量都推导出某个终结符字符串。
推导过程 -
步骤1 - 包括所有推导出某个终结符的符号W1,并初始化i=1。
步骤2 - 包括所有推导出Wi的符号Wi+1。
步骤3 - 增加i并重复步骤2,直到Wi+1 = Wi。
步骤4 - 包括所有包含Wi的产生式规则。
阶段2 - 从CFG G’导出等价的文法G”,使得每个符号都出现在句子形式中。
推导过程 -
步骤1 - 将起始符包含在Y1中,并初始化i = 1。
步骤2 - 包括所有可以从Yi推导出的符号Yi+1,并包括所有已应用的产生式规则。
步骤3 - 增加i并重复步骤2,直到Yi+1 = Yi。
问题
找到等价于文法G的归约文法,该文法具有产生式规则P: S → AC | B, A → a, C → c | BC, E → aA | e
解答
阶段1 -
T = { a, c, e }
W1 = { A, C, E } 来自规则A → a, C → c和E → aA
W2 = { A, C, E } U { S } 来自规则S → AC
W3 = { A, C, E, S } U ∅
由于W2 = W3,我们可以导出G’为:
G’ = { { A, C, E, S }, { a, c, e }, P, {S}}
其中P: S → AC, A → a, C → c , E → aA | e
阶段2 -
Y1 = { S }
Y2 = { S, A, C } 来自规则S → AC
Y3 = { S, A, C, a, c } 来自规则A → a和C → c
Y4 = { S, A, C, a, c }
由于Y3 = Y4,我们可以导出G”为:
G” = { { A, C, S }, { a, c }, P, {S}}
其中P: S → AC, A → a, C → c
删除单元产生式
任何形式为A → B的产生式规则,其中A, B ∈ 非终结符,称为单元产生式。
删除过程 -
步骤1 - 要删除A → B,每当B → x出现在文法中时,将产生式A → x添加到文法规则中。[x ∈ 终结符,x可以为空值]
步骤2 - 从文法中删除A → B。
步骤3 - 从步骤1重复,直到所有单元产生式都被删除。
问题
从以下内容中删除单元产生式:
S → XY, X → a, Y → Z | b, Z → M, M → N, N → a
解答 −
文法中有3个单元产生式:
Y → Z, Z → M, 和 M → N
首先,我们将删除M → N。
由于N → a,我们添加M → a,并删除M → N。
产生式集变为
S → XY, X → a, Y → Z | b, Z → M, M → a, N → a
现在我们将删除Z → M。
由于M → a,我们添加Z→ a,并删除Z → M。
产生式集变为
S → XY, X → a, Y → Z | b, Z → a, M → a, N → a
现在我们将删除Y → Z。
由于Z → a,我们添加Y→ a,并删除Y → Z。
产生式集变为
S → XY, X → a, Y → a | b, Z → a, M → a, N → a
现在Z、M和N不可达,因此我们可以删除它们。
最终的CFG是无单元产生式的:
S → XY, X → a, Y → a | b
删除空产生式
在CFG中,如果存在产生式A → ε或存在从A开始并最终以ε结束的推导,则非终结符‘A’是可空变量
ε: A → .......… → ε
删除过程
步骤1 - 找出推导出ε的可空非终结符变量。
步骤2 - 对于每个产生式A → a,构造所有产生式A → x,其中x是从‘a’中删除步骤1中的一个或多个非终结符得到的。
步骤3 - 将原始产生式与步骤2的结果合并,并删除ε - 产生式。
问题
从以下内容中删除空产生式:
S → ASA | aB | b, A → B, B → b | ∈
解答 −
有两个可空变量:A和B
首先,我们将删除B → ε。
移除B → ε后,产生式集合变为−
S→ASA | aB | b | a, A ε B| b | &epsilon, B → b
现在我们将移除A → ε。
移除A → ε后,产生式集合变为−
S→ASA | aB | b | a | SA | AS | S, A → B| b, B → b
这是最终没有空转移的产生式集合。
乔姆斯基范式
如果产生式具有以下形式,则CFG处于乔姆斯基范式−
- A → a
- A → BC
- S → ε
其中A、B和C是非终结符,而a是终结符。
转换为乔姆斯基范式的算法−
步骤1 − 如果起始符号S出现在某个右部,则创建一个新的起始符号S’和一个新的产生式S’→ S。
步骤2 − 移除空产生式。(使用前面讨论的空产生式移除算法)
步骤3 − 移除单元产生式。(使用前面讨论的单元产生式移除算法)
步骤4 − 将每个产生式A → B1…Bn(其中n > 2)替换为A → B1C,其中C → B2 …Bn。对右部有两个或多个符号的所有产生式重复此步骤。
步骤5 − 如果任何产生式的右部形式为A → aB(其中a是终结符,A, B是非终结符),则将产生式替换为A → XB和X → a。对所有形式为A → aB的产生式重复此步骤。
问题
将以下CFG转换为CNF
S → ASA | aB, A → B | S, B → b | ε
解答
(1) 由于S出现在右部,因此我们添加一个新状态S0,并将S0→S添加到产生式集合中,它变为−
S0→S, S→ ASA | aB, A → B | S, B → b | ∈
(2) 现在我们将移除空产生式−
B → ∈ 和 A → ∈
移除B → ε后,产生式集合变为−
S0→S, S→ ASA | aB | a, A → B | S | ∈, B → b
移除A → ∈后,产生式集合变为−
S0→S, S→ ASA | aB | a | AS | SA | S, A → B | S, B → b
(3) 现在我们将移除单元产生式。
移除S → S后,产生式集合变为−
S0→S, S→ ASA | aB | a | AS | SA, A → B | S, B → b
移除S0→ S后,产生式集合变为−
S0→ ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA
A → B | S, B → b
移除A→ B后,产生式集合变为−
S0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA
A → S | b
B → b
移除A→ S后,产生式集合变为−
S0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA
A → b |ASA | aB | a | AS | SA, B → b
(4) 现在我们将找出右部超过两个变量的产生式
这里,S0→ ASA,S → ASA,A→ ASA违反了右部有两个以上非终结符的规则。
因此,我们将应用步骤4和步骤5以获得以下最终产生式集合,该集合处于CNF−
S0→ AX | aB | a | AS | SA
S→ AX | aB | a | AS | SA
A → b |AX | aB | a | AS | SA
B → b
X → SA
(5) 我们必须更改产生式S0→ aB,S→ aB,A→ aB
最终产生式集合变为−
S0→ AX | YB | a | AS | SA
S→ AX | YB | a | AS | SA
A → b A → b |AX | YB | a | AS | SA
B → b
X → SA
Y → a
格雷巴赫范式
如果产生式具有以下形式,则CFG处于格雷巴赫范式−
A → b
A → bD1…Dn
S → ε
其中A、D1,....,Dn是非终结符,b是终结符。
将CFG转换为格雷巴赫范式的算法
步骤1 − 如果起始符号S出现在某个右部,则创建一个新的起始符号S’和一个新的产生式S’ → S。
步骤2 − 移除空产生式。(使用前面讨论的空产生式移除算法)
步骤3 − 移除单元产生式。(使用前面讨论的单元产生式移除算法)
步骤4 − 移除所有直接和间接左递归。
步骤5 − 对产生式进行适当的替换以将其转换为GNF的正确形式。
问题
将以下CFG转换为CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
解答
这里,S没有出现在任何产生式的右部,并且产生式规则集中没有单元或空产生式。因此,我们可以跳过步骤1到步骤3。
步骤4
现在替换
S → XY | Xo | p中的X
为
mX | m
我们得到
S → mXY | mY | mXo | mo | p。
并且替换
Y → Xn | o中的X
为
X → mX | m
我们得到
Y → mXn | mn | o的右部。
将两个新产生式O → o和P → p添加到产生式集合中,然后我们得到以下最终GNF−
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
CFG的泵引理
引理
如果L是一个上下文无关语言,则存在一个泵长度p,使得长度≥ p的任何字符串w ∈ L可以写成w = uvxyz,其中vy ≠ ε,|vxy| ≤ p,并且对于所有i ≥ 0, uvixyiz ∈ L。
泵引理的应用
泵引理用于检查语法是否为上下文无关。让我们举一个例子并展示如何进行检查。
问题
找出语言L = {xnynzn | n ≥ 1}是否为上下文无关语言。
解答
假设L是上下文无关语言。那么,L必须满足泵引理。
首先,选择泵引理中的一个数字n。然后,将z设为0n1n2n。
将z分解为uvwxy,其中
|vwx| ≤ n 且 vx ≠ ε。
因此,vwx不能同时包含0和2,因为最后一个0和第一个2至少相隔(n+1)个位置。有两种情况−
情况1 − vwx没有2。那么vx仅包含0和1。那么uwy(必须在L中)有n个2,但少于n个0或1。
情况2 − vwx没有0。
这里出现了矛盾。
因此,L不是上下文无关语言。
下推自动机简介
PDA的基本结构
下推自动机是一种以类似于我们为正则语法设计DFA的方式实现上下文无关语法的方法。DFA可以记住有限量的信息,但PDA可以记住无限量的信息。
基本上,下推自动机是−
"有限状态机" + "一个栈"
下推自动机具有三个组件−
- 输入带,
- 控制单元,以及
- 一个大小无限的栈。
栈指针扫描栈顶符号。
栈执行两个操作−
压栈 − 在顶部添加一个新符号。
出栈 − 读取并移除顶部符号。
PDA可能读取也可能不读取输入符号,但它必须在每次转换中读取栈顶。
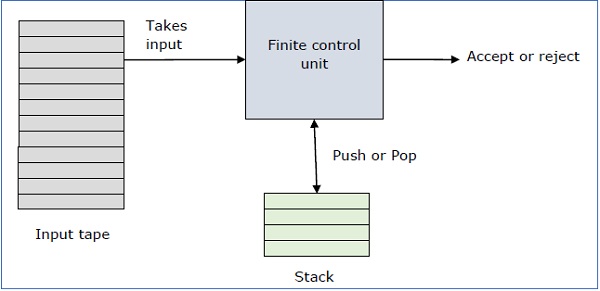
PDA可以正式描述为一个7元组(Q, ∑, S, δ, q0, I, F) −
Q是有限数量的状态
∑是输入字母表
S是栈符号
δ是转换函数:Q × (∑ ∪ {ε}) × S × Q × S*
q0是初始状态(q0 ∈ Q)
I是初始栈顶符号(I ∈ S)
F是接受状态集(F ∈ Q)
下图显示了PDA中从状态q1到状态q2的转换,标记为a,b → c −
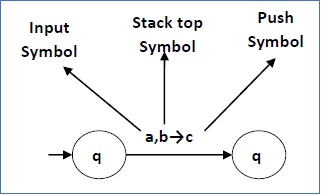
这意味着在状态q1,如果我们遇到输入字符串‘a’并且栈顶符号是‘b’,那么我们将‘b’出栈,将‘c’压入栈顶,并移动到状态q2。
与PDA相关的术语
瞬时描述
PDA的瞬时描述(ID)由三元组(q, w, s)表示,其中
q是状态
w是未消耗的输入
s是栈内容
转向式符号
"转向式"符号用于连接表示PDA的一次或多次移动的ID对。转换过程由转向式符号"⊢"表示。
考虑一个PDA (Q, ∑, S, δ, q0, I, F)。转换可以用以下转向式符号数学表示−
(p, aw, Tβ) ⊢ (q, w, αb)
这意味着在从状态p到状态q进行转换时,输入符号‘a’被消耗,并且栈顶‘T’被新的字符串‘α’替换。
注意 − 如果我们想要PDA的零次或多次移动,则必须使用符号(⊢*)来表示。
下推自动机的接受
有两种不同的方法来定义PDA的可接受性。
终态可接受性
在终态可接受性中,当PDA读取完整个字符串后处于终态时,PDA接受该字符串。从起始状态,我们可以进行导致最终状态的移动,并且栈中的值可以是任意值。只要我们最终处于终态,栈中的值就不相关。
对于PDA (Q, ∑, S, δ, q0, I, F),由终态集F接受的语言为−
L(PDA) = {w | (q0, w, I) ⊢* (q, ε, x), q ∈ F}
对于任何输入栈字符串x。
空栈可接受性
在这里,当PDA读取完整个字符串后,栈为空时,PDA接受该字符串。
对于PDA (Q, ∑, S, δ, q0, I, F),由空栈接受的语言为−
L(PDA) = {w | (q0, w, I) ⊢* (q, ε, ε), q ∈ Q}
示例
构造一个接受L = {0n 1n | n ≥ 0}的PDA
解答
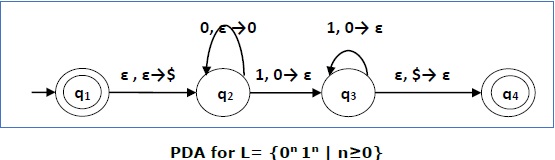
此语言接受L = {ε, 01, 0011, 000111, ............................. }
在这里,在这个例子中,‘a’和‘b’的数量必须相同。
最初,我们将一个特殊符号‘$’放入空栈中。
然后在状态q2,如果我们遇到输入0并且栈顶为空,我们将0压入栈中。这可能会迭代。如果我们遇到输入1并且栈顶是0,我们将此0出栈。
然后在状态q3,如果我们遇到输入1并且栈顶是0,我们将此0出栈。这也会迭代。如果我们遇到输入1并且栈顶是0,我们将出栈栈顶元素。
如果在栈顶遇到特殊符号‘$’,则将其出栈,并最终进入接受状态q4。
示例
构造一个接受L = { wwR | w = (a+b)* }的PDA
解答
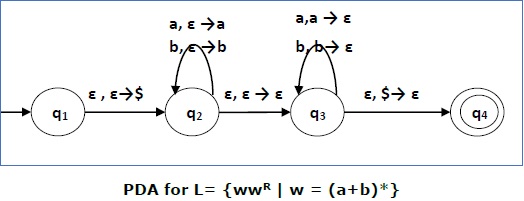
最初,我们将一个特殊符号‘$’放入空栈中。在状态q2,正在读取w。在状态q3,当每个0或1与输入匹配时,将其出栈。如果给出任何其他输入,PDA将进入死状态。当我们到达特殊符号‘$’时,我们将进入接受状态q4。
PDA和上下文无关文法
如果一个文法G是上下文无关的,我们可以构建一个等价的非确定性PDA,该PDA接受由上下文无关文法G产生的语言。可以为文法G构建一个解析器。
此外,如果P是一个下推自动机,则可以构造一个等价的上下文无关文法G,其中
L(G) = L(P)
在接下来的两个主题中,我们将讨论如何将PDA转换为CFG,反之亦然。
找到对应于给定CFG的PDA的算法
输入 − 一个CFG,G = (V, T, P, S)
输出 − 等价的PDA,P = (Q, ∑, S, δ, q0, I, F)
步骤1 − 将CFG的产生式转换为GNF。
步骤2 − PDA只有一个状态{q}。
步骤3 − CFG的起始符号将是PDA中的起始符号。
步骤4 − CFG的所有非终结符将是PDA的栈符号,CFG的所有终结符将是PDA的输入符号。
步骤5 − 对于每个形如A → aX的产生式,其中a是终结符,A, X是非终结符和终结符的组合,创建一个转移δ (q, a, A)。
问题
从以下CFG构建一个PDA。
G = ({S, X}, {a, b}, P, S)
其中产生式为−
S → XS | ε , A → aXb | Ab | ab
解答
令等价的PDA为,
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
其中δ −
δ(q, ε , S) = {(q, XS), (q, ε )}
δ(q, ε , X) = {(q, aXb), (q, Xb), (q, ab)}
δ(q, a, a) = {(q, ε )}
δ(q, 1, 1) = {(q, ε )}
找到对应于给定PDA的CFG的算法
输入 − 一个CFG,G = (V, T, P, S)
输出 − 等价的PDA,P = (Q, ∑, S, δ, q0, I, F),使得语法G的非终结符为{Xwx | w,x ∈ Q},起始状态为Aq0,F。
步骤1 − 对于每个w, x, y, z ∈ Q,m ∈ S以及a, b ∈ ∑,如果δ (w, a, ε)包含(y, m)并且(z, b, m)包含(x, ε),则在语法G中添加产生式规则Xwx → a Xyzb。
步骤2 − 对于每个w, x, y, z ∈ Q,在语法G中添加产生式规则Xwx → XwyXyx。
步骤3 − 对于w ∈ Q,在语法G中添加产生式规则Xww → ε。
下推自动机和解析
解析用于使用语法的产生式规则推导出一个字符串。它用于检查字符串的可接受性。编译器用于检查字符串在语法上是否正确。解析器获取输入并构建语法树。
解析器可以分为两种类型−
自顶向下解析器 − 自顶向下解析从起始符号开始,使用语法树推导出一个字符串。
自底向上解析器 − 自底向上解析从字符串开始,使用语法树到达起始符号。
自顶向下解析器的设计
对于自顶向下解析,PDA有以下四种类型的转移−
弹出栈顶产生式左侧的非终结符,并压入其右侧的字符串。
如果栈顶符号与正在读取的输入符号匹配,则将其弹出。
将起始符号“S”压入栈中。
如果输入字符串已完全读取且栈为空,则进入最终状态“F”。
示例
为表达式“x+y*z”设计一个自顶向下解析器,该表达式对应于具有以下产生式规则的语法G−
P: S → S+X | X, X → X*Y | Y, Y → (S) | id
解答
如果PDA为(Q, ∑, S, δ, q0, I, F),则自顶向下解析为−
(x+y*z, I) ⊢(x +y*z, SI) ⊢ (x+y*z, S+XI) ⊢(x+y*z, X+XI)
⊢(x+y*z, Y+X I) ⊢(x+y*z, x+XI) ⊢(+y*z, +XI) ⊢ (y*z, XI)
⊢(y*z, X*YI) ⊢(y*z, y*YI) ⊢(*z,*YI) ⊢(z, YI) ⊢(z, zI) ⊢(ε, I)
自底向上解析器的设计
对于自底向上解析,PDA有以下四种类型的转移−
将当前输入符号压入栈中。
将栈顶产生式的右侧替换为其左侧。
如果栈顶元素与当前输入符号匹配,则将其弹出。
如果输入字符串已完全读取,并且只有起始符号“S”保留在栈中,则将其弹出并进入最终状态“F”。
示例
为表达式“x+y*z”设计一个自顶向下解析器,该表达式对应于具有以下产生式规则的语法G−
P: S → S+X | X, X → X*Y | Y, Y → (S) | id
解答
如果PDA为(Q, ∑, S, δ, q0, I, F),则自底向上解析为−
(x+y*z, I) ⊢ (+y*z, xI) ⊢ (+y*z, YI) ⊢ (+y*z, XI) ⊢ (+y*z, SI)
⊢(y*z, +SI) ⊢ (*z, y+SI) ⊢ (*z, Y+SI) ⊢ (*z, X+SI) ⊢ (z, *X+SI)
⊢ (ε, z*X+SI) ⊢ (ε, Y*X+SI) ⊢ (ε, X+SI) ⊢ (ε, SI)
图灵机简介
图灵机是一种接受设备,它接受由0型语法生成的语言(递归可枚举集)。它由艾伦·图灵于1936年发明。
定义
图灵机(TM)是一个数学模型,它由一条无限长的带组成,该带被分成单元格,并在其上给出输入。它包含一个读取输入带的磁头。一个状态寄存器存储图灵机的状态。读取输入符号后,将其替换为另一个符号,其内部状态发生变化,并且它从一个单元格移动到右侧或左侧。如果TM到达最终状态,则接受输入字符串,否则拒绝。
TM可以正式描述为一个7元组(Q, X, ∑, δ, q0, B, F),其中−
Q是状态的有限集
X是带字母表
∑是输入字母表
δ是转移函数;δ : Q × X → Q × X × {左移,右移}。
q0是初始状态
B是空白符号
F是最终状态集
与先前自动机的比较
下表显示了图灵机与有限自动机和下推自动机的区别。
| 机器 | 栈数据结构 | 确定性? |
|---|---|---|
| 有限自动机 | N.A | 是 |
| 下推自动机 | 后进先出(LIFO) | 否 |
| 图灵机 | 无限磁带 | 是 |
图灵机的示例
图灵机M = (Q, X, ∑, δ, q0, B, F),其中
- Q = {q0, q1, q2, qf}
- X = {a, b}
- ∑ = {1}
- q0 = {q0}
- B = 空白符号
- F = {qf }
δ由下给出−
| 带字母表符号 | 当前状态“q0” | 当前状态“q1” | 当前状态“q2” |
|---|---|---|---|
| a | 1Rq1 | 1Lq0 | 1Lqf |
| b | 1Lq2 | 1Rq1 | 1Rqf |
这里转移1Rq1表示写入符号为1,磁带向右移动,下一个状态为q1。类似地,转移1Lq2表示写入符号为1,磁带向左移动,下一个状态为q2。
图灵机的时间和空间复杂度
对于图灵机,时间复杂度是指当机器初始化某些输入符号时磁带移动次数的度量,空间复杂度是写入的磁带单元格的数量。
所有合理函数的时间复杂度−
T(n) = O(n log n)
TM的空间复杂度−
S(n) = O(n)
接受语言和判定语言
如果TM对于任何输入字符串w进入最终状态,则它接受该语言。如果语言被图灵机接受,则它是递归可枚举的(由0型语法生成)。
如果TM接受语言并且对于语言中不存在的任何输入进入拒绝状态,则它判定该语言。如果语言被图灵机判定,则它是递归的。
在某些情况下,TM可能不会停止。这样的TM接受语言,但它不判定它。
设计图灵机
下面借助几个例子解释了设计图灵机的一些基本指南。
示例1
设计一个TM来识别所有包含奇数个α的字符串。
解答
图灵机M可以通过以下步骤构建−
令q1为初始状态。
如果M处于q1状态;扫描α时,它进入状态q2并写入B(空白)。
如果M处于q2状态;扫描α时,它进入状态q1并写入B(空白)。
从上述步骤可以看出,如果M扫描偶数个α,则它进入状态q1,如果它扫描奇数个α,则它进入状态q2。因此q2是唯一的接受状态。
因此,
M = {{q1, q2}, {1}, {1, B}, δ, q1, B, {q2}}
其中δ由下给出−
| 带字母表符号 | 当前状态“q1” | 当前状态“q2” |
|---|---|---|
| α | BRq2 | BRq1 |
示例2
设计一个图灵机,读取表示二进制数的字符串,并擦除字符串中的所有前导0。但是,如果字符串仅包含0,则保留一个0。
解答
让我们假设输入字符串以字符串两端的空白符号B结尾。
图灵机M可以通过以下步骤构建−
令q0为初始状态。
如果M处于q0状态,读取0时,它向右移动,进入状态q1并擦除0。读取1时,它进入状态q2并向右移动。
如果M处于q1状态,读取0时,它向右移动并擦除0,即用B替换0。到达最左边的1时,它进入q2并向右移动。如果它到达B,即字符串仅包含0,则它向左移动并进入状态q3。
如果M处于q2状态,读取0或1时,它向右移动。到达B时,它向左移动并进入状态q4。这验证了字符串仅包含0和1。
如果M处于q3状态,它将B替换为0,向左移动并到达最终状态qf。
如果M处于q4状态,无论读取0还是1,它都会向左移动。当到达字符串的开头,即读取B时,它到达最终状态qf。
因此,
M = {{q0, q1, q2, q3, q4, qf}, {0,1, B}, {1, B}, δ, q0, B, {qf}}
其中δ由下给出−
| 带字母表符号 | 当前状态“q0” | 当前状态“q1” | 当前状态“q2” | 当前状态 ‘q3’ | 当前状态 ‘q4’ |
|---|---|---|---|---|---|
| 0 | BRq1 | BRq1 | 或q2 | - | 向左移动至q4 |
| 1 | 1向右移动至q2 | 1向右移动至q2 | 1向右移动至q2 | - | 1向左移动至q4 |
| B | BRq1 | B向左移动至q3 | B向左移动至q4 | 0向左移动至qf | B向右移动至qf |
多磁带图灵机
多磁带图灵机有多个磁带,每个磁带都由一个单独的磁头访问。每个磁头可以独立于其他磁头移动。最初,输入在磁带1上,其他磁带为空白。首先,第一条磁带被输入占用,其他磁带保持空白。接下来,机器读取其磁头下连续的符号,图灵机在每个磁带上打印一个符号并移动其磁头。
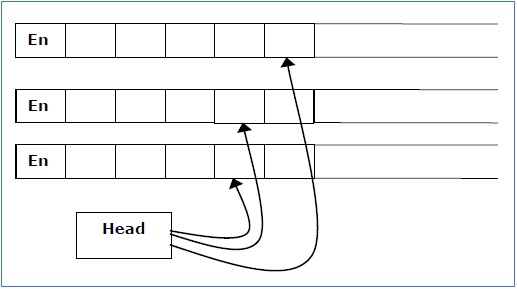
多磁带图灵机可以正式描述为一个6元组 (Q, X, B, δ, q0, F),其中 -
Q是状态的有限集
X是带字母表
B是空白符号
δ 是一个关于状态和符号的关系,其中
δ: Q × Xk → Q × (X × {左移, 右移, 不移动 })k
其中有k个磁带
q0是初始状态
F是最终状态集
注意 - 每个多磁带图灵机都有一个等价的单磁带图灵机。
多轨迹图灵机
多轨迹图灵机,一种特定类型的多磁带图灵机,包含多条轨迹,但只有一个磁头读取和写入所有轨迹。在这里,一个磁头在一个步骤中从n条轨迹读取n个符号。它接受递归可枚举语言,就像普通的单轨单磁带图灵机一样。
多轨迹图灵机可以正式描述为一个6元组 (Q, X, ∑, δ, q0, F),其中 -
Q是状态的有限集
X是带字母表
∑是输入字母表
δ 是一个关于状态和符号的关系,其中
δ(Qi, [a1, a2, a3,....]) = (Qj, [b1, b2, b3,....], 左移 或 右移)
q0是初始状态
F是最终状态集
注意 - 对于每个单轨图灵机S,都存在一个等价的多轨迹图灵机M,使得L(S) = L(M)。
非确定性图灵机
在非确定性图灵机中,对于每个状态和符号,图灵机都可以有一组动作。因此,这里的转换不是确定性的。非确定性图灵机的计算是从起始配置可以到达的配置树。
如果树中至少有一个节点是接受配置,则接受输入,否则不接受。如果计算树的所有分支在所有输入上都停止,则非确定性图灵机称为判定机,如果对于某些输入,所有分支都被拒绝,则该输入也被拒绝。
非确定性图灵机可以正式定义为一个6元组 (Q, X, ∑, δ, q0, B, F),其中 -
Q是状态的有限集
X是带字母表
∑是输入字母表
δ 是一个转移函数;
δ : Q × X → P(Q × X × {左移, 右移}).
q0是初始状态
B是空白符号
F是最终状态集
半无限带图灵机
具有半无限磁带的图灵机有一个左端但没有右端。左端以一个结束标记限制。
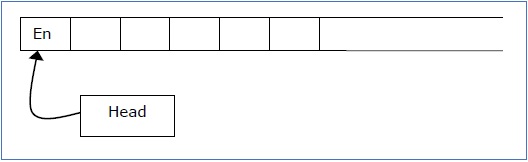
它是一个双轨磁带 -
上轨迹 - 它表示初始磁头位置右侧的单元格。
下轨迹 - 它表示初始磁头位置左侧的单元格,顺序相反。
无限长的输入字符串最初以连续的磁带单元格写入磁带上。
机器从初始状态q0开始,磁头从左端标记“End”开始扫描。在每个步骤中,它读取磁头下磁带上的符号。它在该磁带单元格上写入一个新符号,然后它将磁头向左或向右移动一个磁带单元格。一个转移函数决定要采取的动作。
它有两个特殊状态,称为接受状态和拒绝状态。如果在任何时候它进入接受状态,则接受输入;如果它进入拒绝状态,则图灵机拒绝输入。在某些情况下,它会无限期地运行,而不会被接受或拒绝某些特定的输入符号。
注意 - 具有半无限磁带的图灵机等价于标准图灵机。
线性有界自动机
线性有界自动机是一种多轨迹非确定性图灵机,其磁带具有一定的有界有限长度。
长度 = 函数 (初始输入字符串的长度, 常数 c)
这里,
内存信息 ≤ c × 输入信息
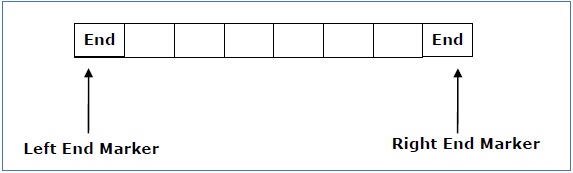
计算被限制在常数有界区域。输入字母表包含两个特殊符号,用作左端标记和右端标记,这意味着转换既不移动到左端标记的左侧,也不移动到磁带右端标记的右侧。
线性有界自动机可以定义为一个8元组 (Q, X, ∑, q0, ML, MR, δ, F),其中 -
Q是状态的有限集
X是带字母表
∑是输入字母表
q0是初始状态
ML 是左端标记
MR 是右端标记,其中 MR ≠ ML
δ 是一个转移函数,它将每个 (状态, 磁带符号) 对映射到 (状态, 磁带符号, 常数 'c'),其中 c 可以是 0 或 +1 或 -1
F是最终状态集
确定性线性有界自动机总是上下文相关的,并且具有空语言的线性有界自动机是不可判定的。
语言可判定性
如果存在一个图灵机接受并停止每个输入字符串w,则称语言可判定或递归。每个可判定语言都是图灵可接受的。
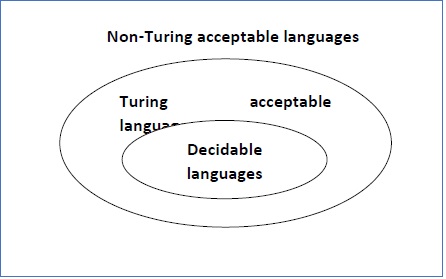
如果所有“是”实例到P的语言L是可判定的,则判定问题P是可判定的。
对于可判定语言,对于每个输入字符串,图灵机要么在接受状态要么在拒绝状态停止,如下面的图所示 -
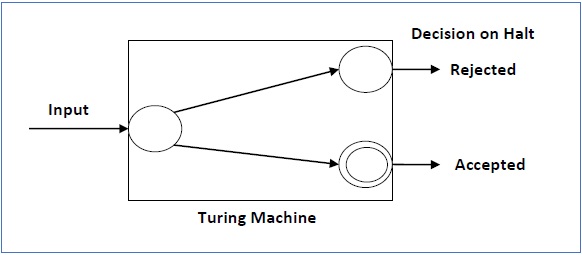
示例1
找出以下问题是否可判定 -
数字“m”是否为素数?
解答
素数 = {2, 3, 5, 7, 11, 13, …………..}
从“2”开始,将数字“m”除以“2”到“√m”之间的所有数字。
如果这些数字中的任何一个产生余数为零,则它进入“拒绝状态”,否则它进入“接受状态”。因此,这里答案可以用“是”或“否”给出。
因此,这是一个可判定问题。
示例2
给定一个正则语言L和字符串w,我们如何检查w ∈ L?
解答
获取接受L的DFA,并检查w是否被接受
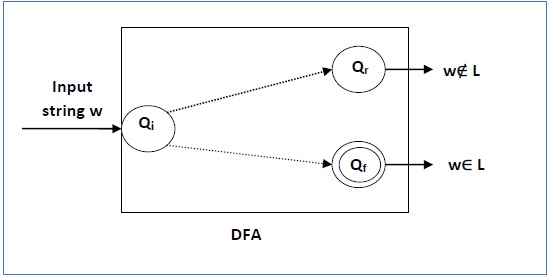
一些其他的可判定问题是 -
- DFA是否接受空语言?
- 对于正则集,L1 ∩ L2 = ∅ 是否成立?
注意 -
如果语言L是可判定的,则其补集L'也是可判定的
如果语言是可判定的,则它有一个枚举器。
不可判定语言
对于不可判定语言,不存在任何图灵机接受该语言并对每个输入字符串w做出决策(尽管图灵机可以对某些输入字符串做出决策)。如果所有“是”实例到P的语言L不可判定,则判定问题P称为“不可判定”。不可判定语言不是递归语言,但有时它们可能是递归可枚举语言。
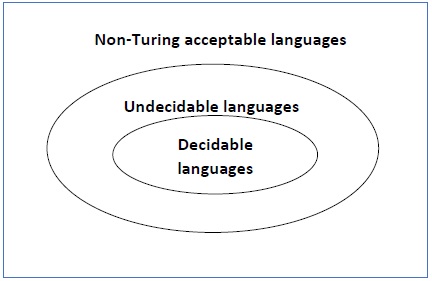
示例
- 图灵机的停机问题
- 死亡问题
- 死亡矩阵问题
- Post对应问题等。
图灵机停机问题
输入 - 图灵机和一个输入字符串w。
问题 - 图灵机是否在有限步数内完成字符串w的计算?答案必须是“是”或“否”。
证明 - 首先,我们将假设存在这样的图灵机来解决这个问题,然后我们将证明它自相矛盾。我们将这个图灵机称为停机机,它在有限的时间内产生“是”或“否”。如果停机机在有限时间内完成,则输出为“是”,否则为“否”。以下是停机机的框图 -
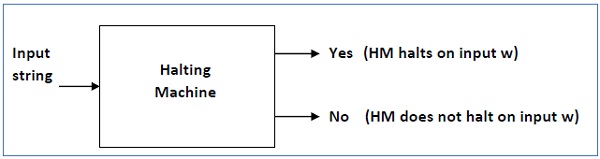
现在我们将设计一个反向停机机 (HM)’ 如下 -
如果H返回YES,则无限循环。
如果H返回NO,则停止。
以下是“反向停机机”的框图 -
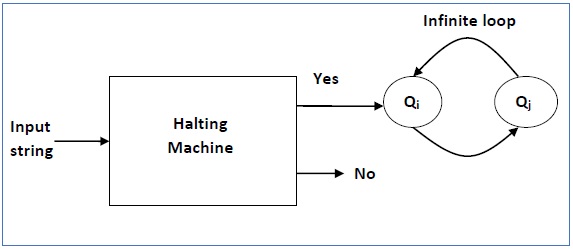
此外,一个输入为自身的机器(HM)2构造如下 -
- 如果 (HM)2 在输入上停止,则无限循环。
- 否则,停止。
这里,我们得到了一个矛盾。因此,停机问题是不可判定的。
Rice定理
Rice定理指出,由图灵机识别的任何语言的非平凡语义属性都是不可判定的。属性 P 是满足该属性的所有图灵机的语言。
形式定义
如果 P 是一个非平凡属性,并且保存该属性的语言 Lp 被图灵机 M 识别,则 Lp = {<M> | L(M) ∈ P} 是不可判定的。
描述和属性
语言的属性 P 仅仅是一组语言。如果任何语言属于 P (L ∈ P),则称 L 满足属性 P。
如果一个属性不被任何递归可枚举语言满足,或者被所有递归可枚举语言满足,则称该属性是平凡的。
非平凡属性被一些递归可枚举语言满足,而被其他语言不满足。正式地说,在一个非平凡属性中,其中 L ∈ P,以下两个属性都成立
属性 1 - 存在图灵机 M1 和 M2 识别相同的语言,即 ( <M1>, <M2> ∈ L ) 或 ( <M1>,<M2> ∉ L )
属性 2 - 存在图灵机 M1 和 M2,其中 M1 识别该语言而 M2 不识别,即 <M1> ∈ L 且 <M2> ∉ L
证明
假设属性 P 是非平凡的,并且 φ ∈ P。
由于 P 是非平凡的,至少有一种语言满足 P,即 L(M0) ∈ P ,∋ 图灵机 M0。
设 w 是一个特定时刻的输入,N 是一个遵循以下规则的图灵机 -
在输入 x 上
- 在 w 上运行 M
- 如果 M 不接受(或不停止),则不接受 x(或不停止)
- 如果 M 接受 w,则在 x 上运行 M0。如果 M0 接受 x,则接受 x。
一个将实例 ATM = {<M,w>| M 接受输入 w} 映射到 N 的函数,使得
- 如果 M 接受 w 且 N 接受与 M0 相同的语言,则 L(M) = L(M0) ∈ p
- 如果 M 不接受 w 且 N 接受 φ,则 L(N) = φ ∉ p
由于 ATM 是不可判定的,并且可以归约到 Lp,因此 Lp 也是不可判定的。
Post对应问题
Post对应问题 (PCP),由 Emil Post 于 1946 年提出,是一个不可判定的决策问题。字母表 ∑ 上的 PCP 问题陈述如下 -
给定以下两个列表M和N,它们是非空字符串在 ∑ 上的列表 -
M = (x1, x2, x3,………, xn)
N = (y1, y2, y3,………, yn)
如果对于某些 i1,i2,………… ik,其中 1 ≤ ij ≤ n,条件 xi1 …….xik = yi1 …….yik 满足,则可以说存在一个Post对应解。
示例1
找出列表
M = (abb, aa, aaa) 和 N = (bba, aaa, aa)
是否具有Post对应解?
解答
| x1 | x2 | x3 | |
|---|---|---|---|
| M | Abb | aa | aaa |
| N | Bba | aaa | aa |
这里,
x2x1x3 = ‘aaabbaaa’
和 y2y1y3 = ‘aaabbaaa’
我们可以看到
x2x1x3 = y2y1y3
因此,解是i = 2, j = 1, 且 k = 3。
示例2
找出列表M = (ab, bab, bbaaa)和N = (a, ba, bab)是否具有Post对应解?
解答
| x1 | x2 | x3 | |
|---|---|---|---|
| M | ab | bab | bbaaa |
| N | a | ba | bab |
在这种情况下,没有解,因为 -
| x2x1x3 | ≠ | y2y1y3 | (长度不相等)
因此,可以说这个Post对应问题是不可判定的。