Arden定理

---

---

为了找出有限自动机的正则表达式，我们使用Arden定理以及正则表达式的性质。

陈述 −

设P和Q为两个正则表达式。

如果P不包含空串，则R = Q + RP 有唯一解R = QP*

证明 −

R = Q + (Q + RP)P [代入R = Q + RP]

= Q + QP + RPP

当我们反复递归地代入R的值时，我们得到以下等式−

R = Q + QP + QP² + QP³…..

R = Q (ε + P + P² + P³ + …. )

R = QP* [因为P*表示(ε + P + P² + P³ + ….)]

因此，得证。

应用Arden定理的假设

• 状态转换图不能有空转移
• 它必须只有一个初始状态

方法

步骤1 − 为具有n个状态和初始状态q₁的DFA的所有状态创建如下形式的等式。

q₁ = q₁R₁₁ + q₂R₂₁ + … + q_nR_n1 + ε

q₂ = q₁R₁₂ + q₂R₂₂ + … + q_nR_n2

…………………………

…………………………

…………………………

…………………………

q_n = q₁R_1n + q₂R_2n + … + q_nR_nn

R_ij表示从q_i到q_j的边的标签集，如果没有这样的边，则R_ij = ∅

步骤2 − 解这些方程以获得最终状态关于R_ij的方程

问题

构造与下面给出的自动机对应的正则表达式−

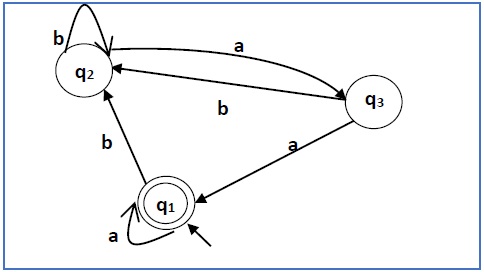
解答 −

这里初始状态和最终状态是q₁。

三个状态q1、q2和q3的方程如下：

q₁ = q₁a + q₃a + ε (ε转移是因为q1是初始状态)

q₂ = q₁b + q₂b + q₃b

q₃ = q₂a

现在，我们将求解这三个方程：

q₂ = q₁b + q₂b + q₃b

= q₁b + q₂b + (q₂a)b (代入q₃的值)

= q₁b + q₂(b + ab)

= q₁b (b + ab)* (应用Arden定理)

q₁ = q₁a + q₃a + ε

= q₁a + q₂aa + ε (代入q₃的值)

= q₁a + q₁b(b + ab*)aa + ε (代入q₂的值)

= q₁(a + b(b + ab)*aa) + ε

= ε (a+ b(b + ab)*aa)*

= (a + b(b + ab)*aa)*

因此，正则表达式是(a + b(b + ab)*aa)*。

问题

构造与下面给出的自动机对应的正则表达式−

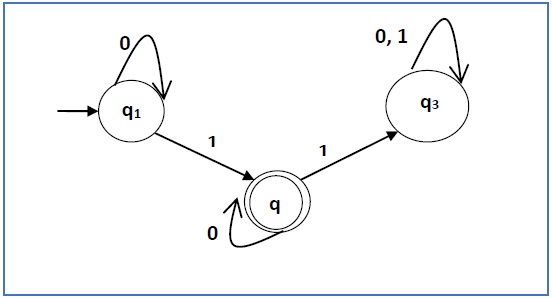
解答 −

这里初始状态是q₁，最终状态是q₂

现在我们写下方程：

q₁ = q₁0 + ε

q₂ = q₁1 + q₂0

q₃ = q₂1 + q₃0 + q₃1

现在，我们将求解这三个方程：

q₁ = ε0* [因为，εR = R]

所以，q₁ = 0*

q₂ = 0*1 + q₂0

所以，q₂ = 0*1(0)* [根据Arden定理]

因此，正则表达式是0*10*。