
- 自动机理论教程
- 自动机理论 - 首页
- 自动机理论 - 入门
- 自动机理论 - 历史
- 自动机理论 - 应用
- 自动机理论术语
- 自动机中字符串的基础
- 自动机的集合论
- 语言和文法
- 计算理论中的文法
- 由文法生成的语言
- 乔姆斯基文法分类
- 有限自动机
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NFA)
- 从NFA到DFA的转换
- DFA的最小化
- 穆尔机与米利机
- DFA的补集
- 正则表达式
- 自动机中的正则表达式
- 自动机中的Arden定理
- 将正则表达式转换为有限自动机
- 正则文法的泵引理
- 计算理论中的正则集
- 上下文无关文法
- 上下文无关文法 (CFG)
- 上下文无关文法中的二义性
- 上下文无关语言的闭包性质
- 简化上下文无关文法
- 乔姆斯基范式 (CNF)
- 格雷巴赫范式 (GNF)
- 上下文无关文法的泵引理
- 下推自动机
- 下推自动机 (PDA)
- 下推自动机的接受
- 从CFG构造PDA
- 下推自动机和语法分析
- 图灵机
- 图灵机 (TM)基础
- 图灵机接受的语言
- 多磁带图灵机
- 多轨迹图灵机
- 非确定性图灵机
- 半无限带图灵机
- 线性有界自动机 (LBA)
- 可计算性和不可判定性
- 图灵语言可判定性
- 不可判定语言
- 图灵机停机问题
- 计算理论中的Rice定理
- Post对应问题 (PCP)
- 自动机理论资源
- 自动机理论 - 快速指南
- 自动机理论 - 资源
- 自动机理论 - 讨论
NFA到DFA的转换
问题陈述
设X = (Qx, ∑, δx, q0, Fx)为一个接受语言L(X)的NFA。我们必须设计一个等价的DFAY = (Qy, ∑, δy, q0, Fy),使得L(Y) = L(X)。以下过程将NFA转换为其等价的DFA -
算法
输入 - 一个NFA
输出 - 一个等价的DFA
步骤1 - 从给定的NFA创建状态表。
步骤2 - 为等价的DFA在可能的输入字母表下创建一个空白状态表。
步骤3 - 将DFA的起始状态标记为q0(与NFA相同)。
步骤4 - 找出每个可能的输入字母表的状态组合{Q0, Q1,... , Qn}。
步骤5 - 每次我们在输入字母表列下生成一个新的DFA状态时,都必须再次应用步骤4,否则转到步骤6。
步骤6 - 包含NFA的任何最终状态的状态是等价DFA的最终状态。
示例
让我们考虑下图所示的NFA。
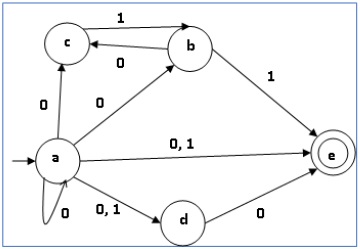
| q | δ(q,0) | δ(q,1) |
|---|---|---|
| a | {a,b,c,d,e} | {d,e} |
| b | {c} | {e} |
| c | ∅ | {b} |
| d | {e} | ∅ |
| e | ∅ | ∅ |
使用上述算法,我们找到其等价的DFA。DFA的状态表如下所示。
| q | δ(q,0) | δ(q,1) |
|---|---|---|
| [a] | [a,b,c,d,e] | [d,e] |
| [a,b,c,d,e] | [a,b,c,d,e] | [b,d,e] |
| [d,e] | [e] | ∅ |
| [b,d,e] | [c,e] | [e] |
| [e] | ∅ | ∅ |
| [c, e] | ∅ | [b] |
| [b] | [c] | [e] |
| [c] | ∅ | [b] |
DFA的状态图如下所示 -
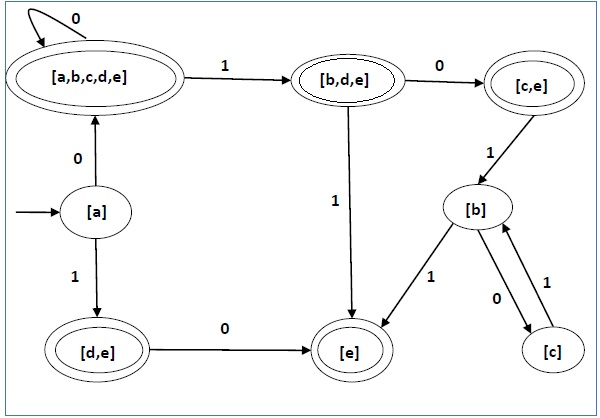
广告