多磁带图灵机

多磁带图灵机有多个磁带，每个磁带都有一个单独的磁头访问。每个磁头可以独立于其他磁头移动。最初，输入在磁带 1 上，其他磁带为空白。首先，第一个磁带被输入占用，其他磁带保持空白。接下来，机器读取磁头下连续的符号，并且 TM 在每个磁带上打印一个符号并移动其磁头。

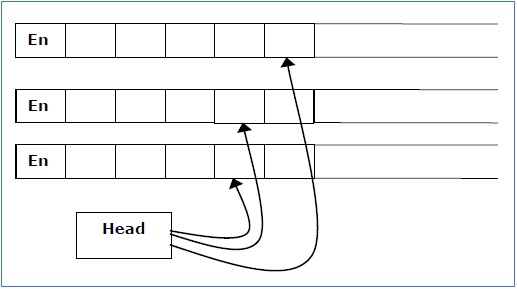
多磁带图灵机可以正式描述为一个 6 元组 (Q, X, B, δ, q₀, F)，其中 -

• Q 是状态的有限集合

• X 是磁带字母表

• B 是空白符号

• δ 是状态和符号上的关系，其中

  δ: Q × X^k → Q × (X × {左移, 右移, 不移})^k

  其中有 k 个磁带

• q₀ 是初始状态

• F 是最终状态的集合

注意 - 每个多磁带图灵机都有一个等价的单磁带图灵机。