上下文无关文法简介

---

---

定义 − 上下文无关文法 (CFG) 由一组有限的语法规则组成，是一个四元组 (N, T, P, S)，其中

• N 是一组非终结符。

• T 是一组终结符，其中 N ∩ T = NULL。

• P 是一组规则，P: N → (N ∪ T)*，即产生式规则 P 的左边没有任何右上下文或左上下文。

• S 是起始符。

示例

• 文法 ({A}, {a, b, c}, P, A)，P：A → aA，A → abc。
• 文法 ({S, a, b}, {a, b}, P, S)，P：S → aSa，S → bSb，S → ε
• 文法 ({S, F}, {0, 1}, P, S)，P：S → 00S | 11F，F → 00F | ε

生成推导树

推导树或语法分析树是一个有序的根树，它以图形方式表示从上下文无关文法导出的字符串的语义信息。

表示技术

• 根顶点 − 必须用起始符标记。

• 顶点 − 用非终结符标记。

• 叶子 − 用终结符或 ε 标记。

如果 S → x₁x₂ …… x_n 是 CFG 中的产生式规则，则语法分析树/推导树如下所示：

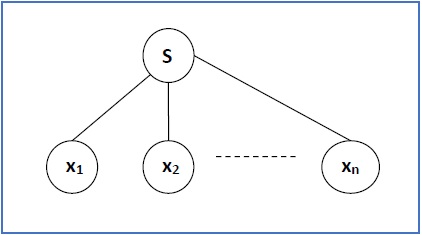
有两种不同的方法可以绘制推导树：

自顶向下方法：

• 从起始符 S 开始

• 使用产生式向下到树叶

自底向上方法：

• 从树叶开始

• 向上进行到根，即起始符 S

树的推导或结果

语法分析树的推导或结果是从左到右连接树叶的标签而获得的最终字符串，忽略空值。但是，如果所有叶子都是空值，则推导为空值。

示例

设 CFG {N,T,P,S} 为

N = {S}，T = {a, b}，起始符 = S，P = S → SS | aSb | ε

来自上述 CFG 的一个推导是“abaabb”

S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

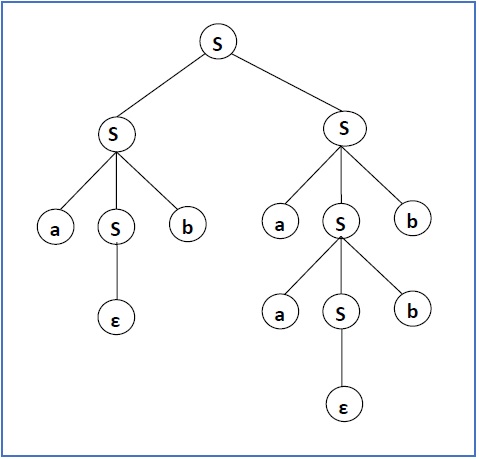
句子形式和部分推导树

部分推导树是推导树/语法分析树的子树，其所有子节点都在子树中或都不在子树中。

示例

如果在任何 CFG 中，产生式为：

S → AB，A → aaA | ε，B → Bb | ε

则部分推导树可以是：

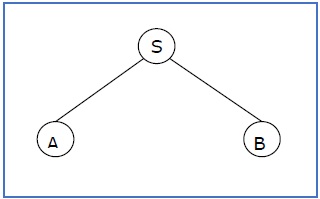
如果部分推导树包含根 S，则称为句子形式。上述子树也处于句子形式。

字符串的最左推导和最右推导

• 最左推导 − 最左推导是通过在每一步都应用产生式到最左边的变量而获得的。

• 最右推导 − 最右推导是通过在每一步都应用产生式到最右边的变量而获得的。

示例

设 CFG 中的任何一组产生式规则为

X → X+X | X*X |X| a

在字母表 {a} 上。

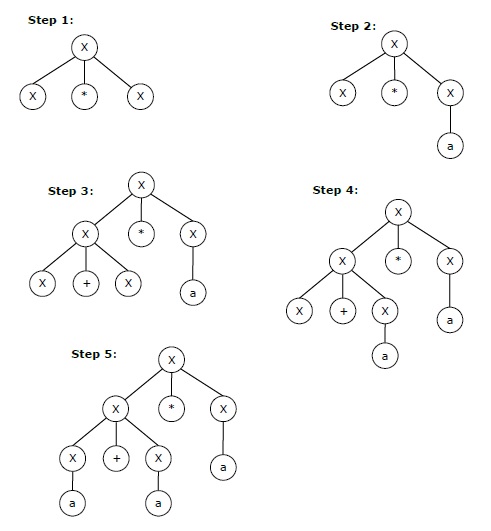
字符串 "a+a*a" 的最左推导可能是：

X → X+X → a+X → a + X*X → a+a*X → a+a*a

上述字符串的分步推导如下所示：

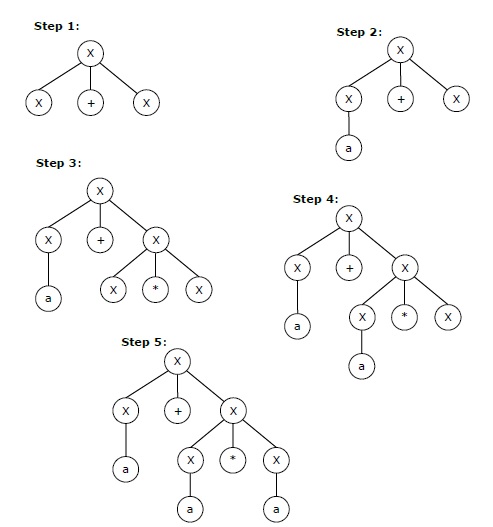
上述字符串 "a+a*a" 的最右推导可能是：

X → X*X → X*a → X+X*a → X+a*a → a+a*a

上述字符串的分步推导如下所示：

左递归文法和右递归文法

在上下文无关文法 G 中，如果存在形式为 X → Xa 的产生式，其中 X 是非终结符，而 ‘a’ 是终结符串，则称为左递归产生式。具有左递归产生式的文法称为左递归文法。

并且，如果在上下文无关文法 G 中，如果存在形式为 X → aX 的产生式，其中 X 是非终结符，而 ‘a’ 是终结符串，则称为右递归产生式。具有右递归产生式的文法称为右递归文法。