
- 自动机理论教程
- 自动机理论 - 首页
- 自动机理论 - 入门
- 自动机理论 - 历史
- 自动机理论 - 应用
- 自动机理论术语
- 自动机中字符串的基础
- 自动机的集合论
- 语言和文法
- 计算理论中的文法
- 由文法生成的语言
- 乔姆斯基文法分类
- 有限自动机
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NFA)
- 从 NFA 到 DFA 的转换
- DFA 的最小化
- Moore 机与 Mealy 机
- DFA 的补集
- 正则表达式
- 自动机中的正则表达式
- 自动机中的 Arden 定理
- 将正则表达式转换为有限自动机
- 正则文法的泵引理
- 计算理论中的正则集
- 上下文无关文法
- 上下文无关文法 (CFG)
- 上下文无关文法中的二义性
- 上下文无关语言的封闭性
- 简化上下文无关文法
- 乔姆斯基范式 (CNF)
- 格雷巴赫范式 (GNF)
- 上下文无关文法的泵引理
- 下推自动机
- 下推自动机 (PDA)
- 下推自动机的接受
- 从 CFG 构造 PDA
- 下推自动机和语法分析
- 图灵机
- 图灵机 (TM) 基础
- 图灵机接受的语言
- 多带图灵机
- 多轨迹图灵机
- 非确定性图灵机
- 半无限带图灵机
- 线性界限自动机 (LBA)
- 可计算性和不可判定性
- 图灵语言的可判定性
- 不可判定语言
- 图灵机停机问题
- 计算理论中的 Rice 定理
- Post 对应问题 (PCP)
- 自动机理论资源
- 自动机理论 - 快速指南
- 自动机理论 - 资源
- 自动机理论 - 讨论
确定性有限自动机
有限自动机可以分为两种类型:
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NDFA / NFA)
确定性有限自动机 (DFA)
在 DFA 中,对于每个输入符号,都可以确定机器将转移到的状态。因此,它被称为确定性自动机。由于它具有有限数量的状态,因此该机器被称为确定性有限机或确定性有限自动机。
DFA 的形式化定义
DFA 可以用一个 5 元组 (Q, ∑, δ, q0, F) 表示,其中:
Q 是一个有限的状态集。
∑ 是一个有限的符号集,称为字母表。
δ 是转移函数,其中 δ: Q × ∑ → Q
q0 是初始状态,从该状态开始处理任何输入 (q0 ∈ Q)。
F 是 Q 的一个或多个最终状态集 (F ⊆ Q)。
DFA 的图形表示
DFA 由称为状态图的有向图表示。
- 顶点表示状态。
- 用输入字母标记的弧表示转移。
- 初始状态用一个空入弧表示。
- 最终状态用双圆圈表示。
示例
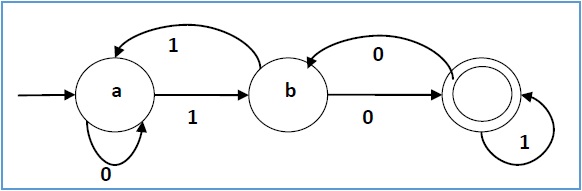
令一个确定性有限自动机为:
- Q = {a, b, c},
- ∑ = {0, 1},
- q0 = {a},
- F = {c}, 以及
转移函数 δ 如下表所示:
| 当前状态 | 输入 0 的下一个状态 | 输入 1 的下一个状态 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
其图形表示如下:
广告