从正则表达式构造有限自动机

---

---

我们可以使用汤姆逊构造法从正则表达式中找出有限自动机。我们将把正则表达式简化为最小的正则表达式，并将这些表达式转换为NFA，最后转换为DFA。

一些基本的RA表达式如下：

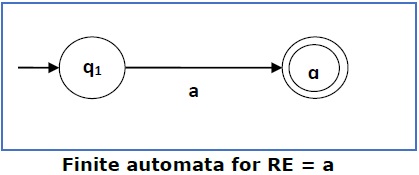
情况1 - 对于正则表达式“a”，我们可以构造以下FA：

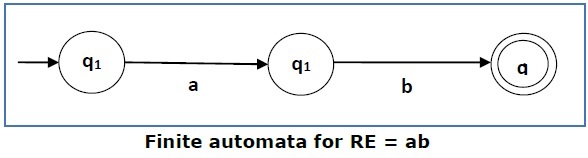
情况2 - 对于正则表达式“ab”，我们可以构造以下FA：

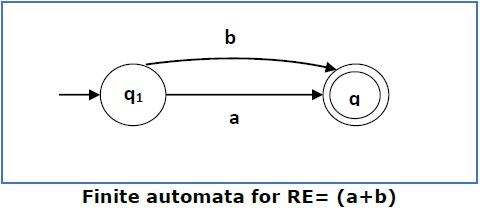
情况3 - 对于正则表达式(a+b)，我们可以构造以下FA：

情况4 - 对于正则表达式(a+b)*，我们可以构造以下FA：

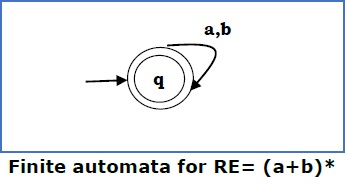
方法

步骤1 从给定的正则表达式构造一个带有空移动的NFA。

步骤2 去除NFA中的空转移，并将其转换为等价的DFA。

问题

将以下RA转换为等价的DFA：1(0+1)*0

解决方案

我们将连接三个表达式“1”、“(0+1)*”和“0”。

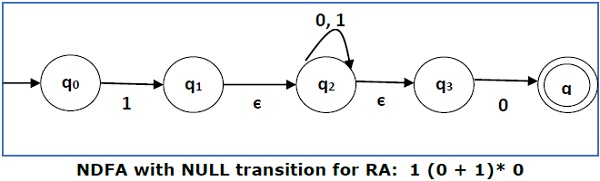
现在我们将移除ε转移。在从NDFA中移除ε转移后，我们得到以下结果：

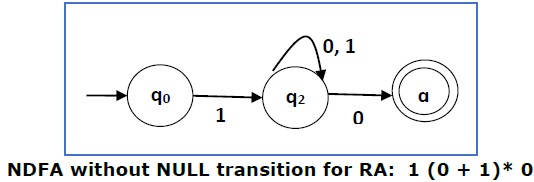
这是一个对应于RE - 1(0+1)*0的NDFA。如果要将其转换为DFA，只需应用第1章中讨论的将NDFA转换为DFA的方法。

带有空移动的有限自动机 (NFA-ε)

带有空移动的有限自动机 (FA-ε) 不仅在从字母集接收输入后转换，而且在没有任何输入符号的情况下转换。这种无需输入的转换称为空移动。

NFA-ε 由一个 5 元组 (Q, ∑, δ, q₀, F) 形式表示，包括

• Q - 一个有限的状态集

• ∑ - 一个有限的输入符号集

• δ - 一个转移函数 δ : Q × (∑ ∪ {ε}) → 2^Q

• q₀ - 一个初始状态 q₀ ∈ Q

• F - Q 的一组最终状态/状态 (F⊆Q)。

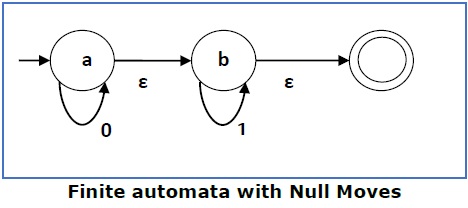
上述(FA-ε) 接受一个字符串集 - {0, 1, 01}

从有限自动机中移除空移动

如果在一个NDFA中，顶点X到顶点Y之间存在ϵ-移动，我们可以使用以下步骤将其移除：

• 查找从Y发出的所有边。
• 复制从X开始的所有这些边，而不更改边标签。
• 如果X是初始状态，则使Y也成为初始状态。
• 如果Y是最终状态，则使X也成为最终状态。

问题

将以下NFA-ε 转换为没有空移动的NFA。

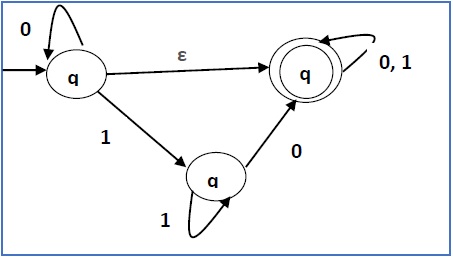
解决方案

步骤1 -

这里 ε 转移在q₁和q₂之间，所以设q₁为X，q_f为Y。

这里从q_f发出的边是对于输入0和1到q_f。

步骤2 -

现在我们将复制从q₁开始的所有这些边，而不更改从q_f开始的边，并获得以下FA：

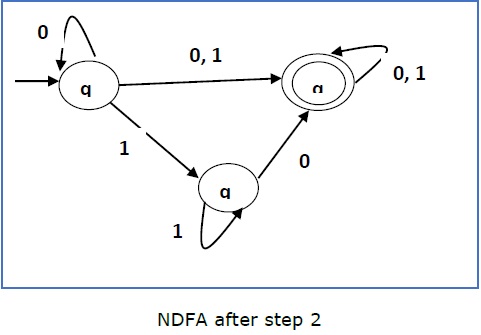
步骤3 -

这里q₁是初始状态，所以我们也使q_f成为初始状态。

所以FA变为：

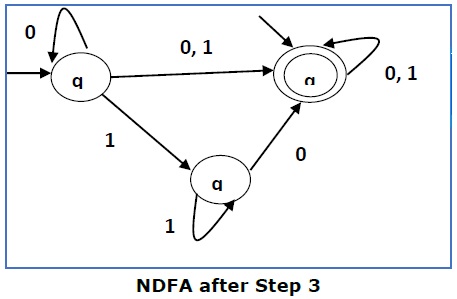
步骤4 -

这里q_f是最终状态，所以我们也使q₁成为最终状态。

所以FA变为：