
- 自动机理论教程
- 自动机理论 - 首页
- 自动机理论 - 入门
- 自动机理论 - 历史
- 自动机理论 - 应用
- 自动机理论术语
- 自动机中字符串的基础知识
- 自动机的集合论
- 语言和文法
- 计算理论中的文法
- 由文法生成的语言
- 乔姆斯基文法分类
- 有限自动机
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NFA)
- 从 NFA 到 DFA 的转换
- DFA 的最小化
- 穆尔机与米利机
- DFA 的补集
- 正则表达式
- 自动机中的正则表达式
- 自动机中的 Arden 定理
- 将正则表达式转换为有限自动机
- 正则文法的泵引理
- 计算理论中的正则集
- 上下文无关文法
- 上下文无关文法 (CFG)
- 上下文无关文法中的二义性
- 上下文无关语言的封闭性
- 简化上下文无关文法
- 乔姆斯基范式 (CNF)
- 格雷巴赫范式 (GNF)
- 上下文无关文法的泵引理
- 下推自动机
- 下推自动机 (PDA)
- 下推自动机的接受
- 由 CFG 构造 PDA
- 下推自动机和解析
- 图灵机
- 图灵机 (TM) 基础
- 图灵机接受的语言
- 多磁带图灵机
- 多轨迹图灵机
- 非确定性图灵机
- 半无限带图灵机
- 线性界自动机 (LBA)
- 可计算性和不可判定性
- 图灵语言的可判定性
- 不可判定语言
- 图灵机停机问题
- 计算理论中的 Rice 定理
- Post 对应问题 (PCP)
- 自动机理论资源
- 自动机理论 - 快速指南
- 自动机理论 - 资源
- 自动机理论 - 讨论
非确定有限自动机
在 NDFA 中,对于特定的输入符号,机器可以移动到机器中任何状态的组合。换句话说,无法确定机器移动到的确切状态。因此,它被称为非确定自动机。因为它具有有限数量的状态,所以该机器被称为非确定有限机或非确定有限自动机。
NDFA 的形式化定义
NDFA 可以用 5 元组 (Q, ∑, δ, q0, F) 表示,其中 -
Q 是一个有限的状态集。
∑ 是一个有限的符号集,称为字母表。
δ 是转移函数,其中 δ: Q × ∑ → 2Q
(这里取 Q 的幂集 (2Q),因为在 NDFA 的情况下,从一个状态可以发生到 Q 状态的任何组合的转移)
q0 是处理任何输入的初始状态 (q0 ∈ Q)。
F 是 Q 的最终状态集 (F ⊆ Q)。
NDFA 的图形表示:(与 DFA 相同)
NDFA 用称为状态图的有向图表示。
- 顶点表示状态。
- 用输入字母标记的弧表示转移。
- 初始状态用空单个传入弧表示。
- 最终状态用双圆圈表示。
示例
令一个非确定性有限自动机为 →
- Q = {a, b, c}
- ∑ = {0, 1}
- q0 = {a}
- F = {c}
转移函数 δ 如下所示 -
| 当前状态 | 输入 0 的下一个状态 | 输入 1 的下一个状态 |
|---|---|---|
| a | a, b | b |
| b | c | a, c |
| c | b, c | c |
它的图形表示如下所示 -
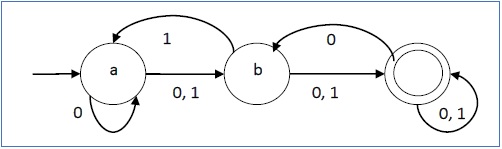
DFA 与 NDFA
下表列出了 DFA 和 NDFA 之间的区别。
| DFA | NDFA |
|---|---|
| 从一个状态的转移对于每个输入符号都是到单个特定下一个状态。因此,它被称为确定性。 | 从一个状态的转移对于每个输入符号可以是到多个下一个状态。因此,它被称为非确定性。 |
| DFA 中没有看到空字符串转移。 | NDFA 允许空字符串转移。 |
| DFA 允许回溯 | 在 NDFA 中,回溯并不总是可能的。 |
| 需要更多空间。 | 需要更少空间。 |
| 如果一个字符串转移到最终状态,则 DFA 接受该字符串。 | 如果所有可能的转移中至少有一个以最终状态结束,则 NDFA 接受一个字符串。 |
接受器、分类器和变换器
接受器(识别器)
计算布尔函数的自动机称为接受器。接受器的所有状态要么接受要么拒绝给它的输入。
分类器
分类器具有两个以上的最终状态,并且在终止时给出单个输出。
变换器
根据当前输入和/或先前状态产生输出的自动机称为变换器。变换器可以分为两种类型 -
米利机 - 输出取决于当前状态和当前输入。
穆尔机 - 输出仅取决于当前状态。
DFA 和 NDFA 的可接受性
当且仅当 DFA/NDFA 从初始状态开始,在完全读取字符串后结束于接受状态(任何最终状态)时,DFA/NDFA 接受一个字符串。
如果 DFA/NDFA (Q, ∑, δ, q0, F) 接受字符串 S,则
δ*(q0, S) ∈ F
DFA/NDFA 接受的语言L 是
{S | S ∈ ∑* 且 δ*(q0, S) ∈ F}
如果 DFA/NDFA (Q, ∑, δ, q0, F) 不接受字符串 S′,则
δ*(q0, S′) ∉ F
DFA/NDFA 不接受的语言 L′(接受语言 L 的补集)是
{S | S ∈ ∑* 且 δ*(q0, S) ∉ F}
示例
让我们考虑图 1.3 中所示的 DFA。从 DFA 中,可以导出可接受的字符串。
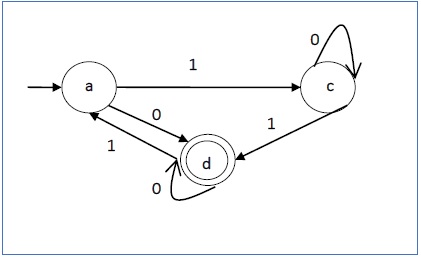
上述 DFA 接受的字符串:{0, 00, 11, 010, 101, ...........}
上述 DFA 不接受的字符串:{1, 011, 111, ........}