
- 自动机理论教程
- 自动机理论 - 首页
- 自动机理论 - 入门
- 自动机理论 - 历史
- 自动机理论 - 应用
- 自动机理论术语
- 自动机中字符串的基础知识
- 自动机的集合论
- 语言和文法
- 计算理论中的文法
- 由文法生成的语言
- 乔姆斯基文法分类
- 有限自动机
- 确定性有限自动机 (DFA)
- 非确定性有限自动机 (NFA)
- 从 NFA 到 DFA 的转换
- DFA 的最小化
- Moore 机与 Mealy 机
- DFA 的补集
- 正则表达式
- 自动机中的正则表达式
- 自动机中的 Arden 定理
- 将正则表达式转换为有限自动机
- 正则文法的泵引理
- 计算理论中的正则集
- 上下文无关文法
- 上下文无关文法 (CFG)
- 上下文无关文法中的二义性
- 上下文无关语言的闭包性质
- 简化上下文无关文法
- 乔姆斯基范式 (CNF)
- 格雷巴赫范式 (GNF)
- 上下文无关文法的泵引理
- 下推自动机
- 下推自动机 (PDA)
- 下推自动机的接受
- 由 CFG 构造 PDA
- 下推自动机和语法分析
- 图灵机
- 图灵机 (TM) 基础知识
- 图灵机接受的语言
- 多磁带图灵机
- 多轨迹图灵机
- 非确定性图灵机
- 半无限磁带图灵机
- 线性有界自动机 (LBA)
- 可计算性和不可判定性
- 图灵语言的可判定性
- 不可判定语言
- 图灵机停机问题
- 计算理论中的 Rice 定理
- Post 对应问题 (PCP)
- 自动机理论资源
- 自动机理论 - 快速指南
- 自动机理论 - 资源
- 自动机理论 - 讨论
DFA 最小化
使用 Myhill-Nerode 定理进行 DFA 最小化
算法
输入 - DFA
输出 - 最小化的 DFA
步骤 1 - 为所有状态对 (Qi, Qj) 绘制表格,这些状态对不一定直接连接 [最初所有状态均未标记]
步骤 2 - 考虑 DFA 中的每个状态对 (Qi, Qj),其中 Qi ∈ F 且 Qj ∉ F 或反之,并标记它们。[此处 F 是最终状态集]
步骤 3 - 重复此步骤,直到我们无法再标记任何状态 -
如果存在未标记的状态对 (Qi, Qj),则如果对于某个输入字母表,状态对 {δ (Qi, A), δ (Qi, A)} 被标记,则标记它。
步骤 4 - 将所有未标记的状态对 (Qi, Qj) 组合起来,并使它们成为简化后的 DFA 中的单个状态。
示例
让我们使用算法 2 来最小化下面显示的 DFA。
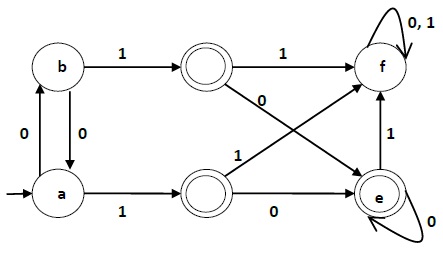
步骤 1 - 我们为所有状态对绘制表格。
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| f |
步骤 2 - 我们标记状态对。
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ |
步骤 3 - 我们将尝试传递地标记状态对,用绿色复选标记。如果我们将 1 输入到状态“a”和“f”,它将分别转到状态“c”和“f”。(c, f) 已被标记,因此我们将标记对 (a, f)。现在,我们将 1 输入到状态“b”和“f”;它将分别转到状态“d”和“f”。(d, f) 已被标记,因此我们将标记对 (b, f)。
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ | ✔ | ✔ |
步骤 3 之后,我们得到了未标记的状态组合 {a, b} {c, d} {c, e} {d, e}。
我们可以将 {c, d} {c, e} {d, e} 重新组合为 {c, d, e}
因此我们得到了两个组合状态 - {a, b} 和 {c, d, e}
因此,最终最小化的 DFA 将包含三个状态 {f}、{a, b} 和 {c, d, e}
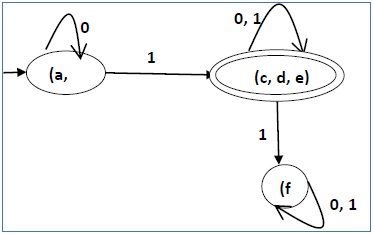
使用等价定理进行 DFA 最小化
如果 X 和 Y 是 DFA 中的两个状态,如果它们不可区分,我们可以将这两个状态组合成 {X, Y}。如果至少存在一个字符串 S,使得 δ (X, S) 和 δ (Y, S) 中的一个是接受状态而另一个不是接受状态,则这两个状态是可区分的。因此,当且仅当所有状态都可区分时,DFA 才是最小的。
算法 3
步骤 1 - 所有状态 Q 分为两个分区 - 最终状态和非最终状态,并表示为 P0。分区中的所有状态都是 0th 等价的。取一个计数器 k 并将其初始化为 0。
步骤 2 - 将 k 加 1。对于 Pk 中的每个分区,如果它们是 k 可区分的,则将 Pk 中的状态划分为两个分区。如果存在输入 S 使得 δ(X, S) 和 δ(Y, S) 是 (k-1) 可区分的,则此分区中的两个状态 X 和 Y 是 k 可区分的。
步骤 3 - 如果 Pk ≠ Pk-1,则重复步骤 2,否则转到步骤 4。
步骤 4 - 将 kth 等价集组合起来,并将它们作为简化后的 DFA 的新状态。
示例
让我们考虑以下 DFA -
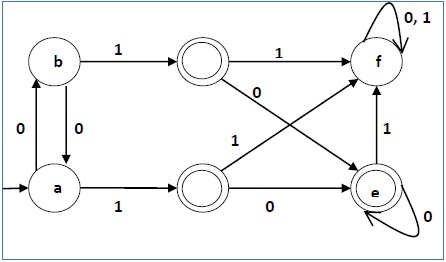
| q | δ(q,0) | δ(q,1) |
|---|---|---|
| a | b | c |
| b | a | d |
| c | e | f |
| d | e | f |
| e | e | f |
| f | f | f |
让我们将上述算法应用于上述 DFA -
- P0 = {(c,d,e), (a,b,f)}
- P1 = {(c,d,e), (a,b),(f)}
- P2 = {(c,d,e), (a,b),(f)}
因此,P1 = P2。
简化后的 DFA 中有三个状态。简化后的 DFA 如下所示 -
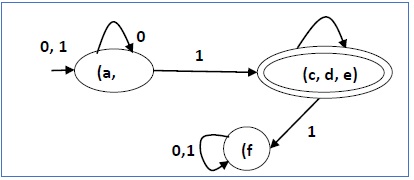
| Q | δ(q,0) | δ(q,1) |
|---|---|---|
| (a, b) | (a, b) | (c,d,e) |
| (c,d,e) | (c,d,e) | (f) |
| (f) | (f) | (f) |