数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究构造一个底边为 8 厘米，高为 4 厘米的等腰三角形，然后构造另一个三角形，其各边长是该等腰三角形对应边的 1½ 倍。
已知
一个底边为 \( 8 \mathrm{~cm} \)，高为 \( 4 \mathrm{~cm} \) 的等腰三角形。
要求
我们必须构造一个底边为 \( 8 \mathrm{~cm} \)，高为 \( 4 \mathrm{~cm} \) 的等腰三角形，然后构造另一个三角形，其各边长是该等腰三角形对应边的 \( 1\frac{1}{2} \) 倍。
解
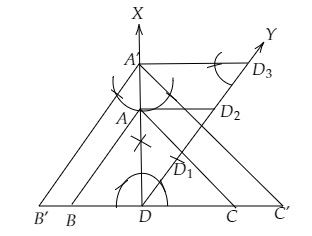
作图步骤
(i) 画一条线段 $BC = 8\ cm$，并作其垂直平分线 $DX$，并在 $DX$ 上截取 $DA = 4\ cm$。
(ii) 连接 $AB$ 和 $AC$。
$ABC$ 是所求三角形。
(iii) 画一条射线 $DY$，使其与 $OA$ 成锐角，并截取三等份，使得 $DD_1 = D_1D_2 =D_2D_3 = D_3D_4$
(iv) 连接 $D_2A$
(v) 画 $D_3A’$ 平行于 $D_2A$，$A’B’$ 平行于 $AB$，分别交 $BC$ 于 $C’$ 和 $B’$。
$B’A’C’$ 是所求三角形。
更新于: 2022年10月10日
69 次浏览
广告