三相感应电动机的特性

三相感应电机的运行性能可以用以下两个特性来解释：

• 转矩-滑差特性

• 转矩-速度特性

三相感应电机的转矩-滑差特性

三相感应电机的**转矩-滑差特性**是电机转矩和滑差在特定转子电阻值下绘制的曲线。图1显示了典型三相感应电机在滑差范围为s = 0到s = 1的不同转子电阻值下的不同转矩-滑差特性。

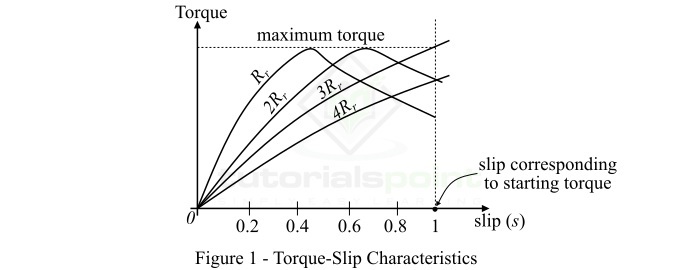
对于三相感应电机，运行条件下电机转矩和滑差之间的关系由下式给出：

$$ \mathrm{\mathit{\tau _{r}}\:=\:\frac{\mathit{KsR_{r}}}{\mathit{R_{r}^{\mathrm{2}}+s^{\mathrm{2}}X_{r}^{\mathrm{2}}}}\:\cdot \cdot \cdot (1)} $$

其中，**K** 是常数，s 是滑差，$\mathit{R_{r}}$ 是每相转子电阻，$\mathit{X_{r}}$ 是每相静止转子电抗。

从公式1，我们可以得出以下几点：

情况1

如果s = 0，则$\mathit{\tau _{r}}\:=\:0$。因此，转矩-滑差曲线从原点开始。

情况2

在电机的正常速度下，滑差很小，因此$\mathit{sX_{r}}$与$\mathit{R_{r}}$相比可以忽略不计。

$$ \mathrm{\therefore \mathit{\tau _{r}}\propto \mathit{\frac{s}{R_{r}}}} $$

由于对于给定的电机，$\mathit{R_{r}}$也是常数。

$$ \mathrm{\therefore \mathit{\tau _{r}}\propto \mathit{s}} $$

因此，转矩-滑差曲线是从零滑差到对应于满载滑差的直线。

情况3

如果滑差值超过满载滑差，则转矩增加，当$\mathit{R _{r}}\:=\:\mathit{s\:X_{r}}$时达到最大值。三相感应电机中的这个最大转矩称为**击穿转矩**或**拉出转矩**。当感应电机在额定电压和频率下运行时，击穿转矩的值至少是满载转矩的两倍。

情况4

当滑差值大于对应于最大转矩的滑差值时，$\mathit{s^{\mathrm{2}}\:X_{r}^{\mathrm{2}}}$项迅速增加，因此$\mathit{R_{r}^{\mathrm{2}}}$可以忽略不计。

$$ \mathrm{\therefore \mathit{\tau _{r}}\propto \mathit{\frac{s}{s^{\mathrm{2}}X_{r}^{\mathrm{2}}}}} $$

由于$\mathit{X_{r}^{\mathrm{2}}}$实际上是常数，则

$$ \mathrm{\mathit{\tau _{r}}\propto \mathit{\frac{\mathrm{1}}{s}}} $$

因此，转矩现在与滑差成反比。因此，转矩-滑差曲线是矩形双曲线。

因此，从以上对三相感应电机转矩-滑差特性的分析可以看出，向转子电路增加电阻不会改变最大转矩的值，而只会改变发生最大转矩的滑差值。

三相感应电机的转矩-速度特性

对于三相感应电机，电机转矩取决于速度，但我们不能用简单的数学方程来表达它们之间的关系。因此，我们使用转矩-速度特性曲线来显示这种关系。图2显示了三相感应电机的典型转矩-速度特性曲线。

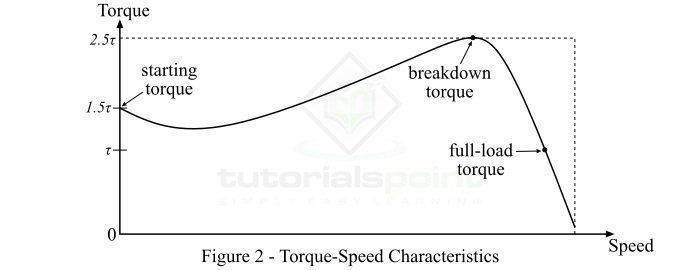
从该特性曲线可以看出以下几点：

• 如果满载转矩为$\tau$，则启动转矩为$1.5\tau$，最大转矩（或击穿转矩）为$2.5\tau$

• 在满载情况下，如果电机的速度为N，如果轴上的机械负载增加，电机的速度将下降，直到电机转矩再次等于负载转矩。一旦两个转矩相等，电机将以恒定速度运行，但低于之前的速度。然而，如果电机转矩大于$2.5\tau$（即击穿转矩），电机将突然停止。

• 对于三相感应电机，转矩-速度曲线在空载和满载点之间基本上是一条直线。曲线线的斜率取决于转子电路的电阻，即电阻越大，斜率越陡。