
- 电机教程
- 电机 - 首页
- 基本概念
- 机电能量转换
- 储存在磁场中的能量
- 单激发和双激发系统
- 旋转电机
- 法拉第电磁感应定律
- 感应电动势的概念
- 弗莱明左手定则和右手定则
- 变压器
- 电力变压器
- 变压器的构造
- 变压器的电动势方程
- 变压比和电压变换比
- 理想变压器和实际变压器
- 直流变压器
- 变压器的损耗
- 变压器的效率
- 三相变压器
- 变压器的类型
- 直流电机
- 直流电机的构造
- 直流电机的类型
- 直流发电机的原理
- 直流发电机的电动势方程
- 直流发电机的类型
- 直流电机的原理
- 直流电机中的反电动势
- 直流电机的类型
- 直流电机的损耗
- 直流电机的应用
- 感应电机
- 感应电机的介绍
- 单相感应电机
- 三相感应电机
- 三相感应电机的构造
- 三相感应电机负载运行
- 三相感应电机的特性
- 调速和速度控制
- 三相感应电机的启动方法
- 同步电机
- 三相同步电机的介绍
- 同步电机的构造
- 三相交流发电机的运行原理
- 同步电机中的电枢反应
- 三相交流发电机的输出功率
- 三相交流发电机的损耗和效率
- 三相同步电机的运行原理
- 同步电机的等效电路和功率因数
- 同步电机产生的功率
- 电机资源
- 电机快速指南
- 电机 - 资源
- 电机 - 讨论
电机快速指南
机电能量转换
如今,电能是应用最广泛的一种能量形式,用于执行各种工业、商业和家用功能,例如抽水、风扇、冷却器、空调、制冷等。由于大多数工艺都需要将电能转换为机械能,同时机械能也转换为电能。因此,我们需要一种机制来将电能转换为机械能,并将机械能转换为电能,这种机制被称为机电能量转换装置。
机电能量转换装置
因此,能够将电能转换为机械能或将机械能转换为电能的装置称为机电能量转换装置。电动发电机和电动机是机电能量转换装置的例子。
在任何机电能量转换装置中,电能与机械能的相互转换都是通过电场或磁场作为媒介进行的。然而,在大多数实际的机电能量转换装置中,磁场用作电气系统和机械系统之间的耦合介质。
机电能量转换装置可分为两类:
大运动装置(如电机和发电机)
增量运动装置(如电磁继电器、测量仪器、扬声器等)
将电能转换为机械能的装置称为电动机。将机械能转换为电能的装置称为发电机。
在电动机中,当载流导体置于变化的(或旋转的)磁场中时,导体会受到机械力。在发电机的情况下,当导体在磁场中运动时,导体中会感应出电动势。尽管这两种电磁效应同时发生,但能量转换在所有机电能量转换装置中都是从电能到机械能,反之亦然。
能量平衡方程
能量平衡方程是一个表达式,它显示了能量转换的完整过程。在机电能量转换装置中,总输入能量等于三个分量的总和:
能量耗散或损失
储存的能量
有用输出能量
因此,对于电动机,能量平衡方程可以写成:
Electrical energy input = Energy dissipated + Energy stored + Mechanical energy output
其中:
电能输入是从主电源提供的电力。
储存的能量等于储存在磁场中的能量以及以势能和动能形式储存在机械系统中的能量之和。
能量耗散等于电阻损耗、磁芯损耗(磁滞损耗+涡流损耗)和机械损耗(风损和摩擦损耗)之和。
对于发电机,能量平衡方程可以写成:
Mechanical energy input = Electrical energy output + Energy stored + Energy dissipated
其中,机械能输入是从涡轮机、发动机等获得的机械能,用于旋转发电机的轴。
储存在磁场中的能量
在上一章中,我们讨论了在机电能量转换装置中,电气系统和机械系统之间存在耦合介质。在大多数实际装置中,磁场用作耦合介质。因此,机电能量转换装置包括一个电磁系统。因此,储存在耦合介质中的能量是以磁场的形式存在的。我们可以计算如下所述的机电能量转换系统的磁场中储存的能量。
考虑一个具有 *N* 个导线匝数的线圈绕在一个磁芯上,如图 1 所示。该线圈由 *v* 伏特的电压源供电。
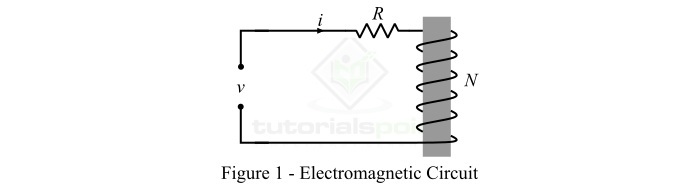
通过应用基尔霍夫电压定律 (KVL),施加到线圈的电压由下式给出:
$$\mathrm{\mathit{V\:=\:e\:+\:iR}\cdot \cdot \cdot (1)}$$
其中:
e 是由于电磁感应而在线圈中感应的电动势。
R 是线圈电路的电阻。
$\mathit{i}$ 是流过线圈的电流。
电磁系统的瞬时功率输入由下式给出:
$$\mathrm{\mathit{p}\:=\:\mathit{Vi\:=\:i\left ( e+iR \right )}}$$
$$\mathrm{\Rightarrow \mathit{p}\:=\:\mathit{ie+ i^{\mathrm{2}}}\mathit{R}\cdot \cdot \cdot (2)}$$
现在,假设在时间 *t* = 0 时将直流电压施加到电路,并在时间 *t* = *t1* 秒结束时,电路中的电流达到 *I* 安培。然后,在此时间间隔内,系统输入的能量由下式给出:
$$\mathrm{\mathit{W}_{in}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{p\:dt}}$$
$$\mathrm{\Rightarrow \mathit{W}_{in}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{ie\:dt}\:+\:\int_{0}^{t_{\mathrm{1}}}\mathit{i^{\mathrm{2}}R\:dt}\cdot \cdot \cdot (3)}$$
从公式 3 可以看出,总输入能量由两部分组成:
第一部分是储存在磁场中的能量。
第二部分是由于线圈的电阻而耗散的能量。
因此,储存在系统磁场中的能量为:
$$\mathrm{\mathit{W}_{\mathit{f}}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{ie\:dt}\:\cdot \cdot \cdot (4)}$$
根据法拉第电磁感应定律,我们有:
$$\mathrm{\mathit{e}\:=\:\frac{\mathit{d\psi }}{\mathit{dt}}\:=\:\frac{\mathit{d}}{\mathit{dt}}\left ( \mathit{N\phi } \right )\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\cdot \cdot \cdot (5)}$$
其中,$\psi$ 是磁通链,等于 $\mathit{\psi \:=\:N\phi }$.
$$\mathrm{\therefore \mathit{W_{f}}\:=\:\int_{0}^{\mathit{t_{\mathrm{1}}}}\frac{\mathit{d\psi }}{\mathit{dt}}\mathit{i\:dt}}$$
$$\mathrm{\Rightarrow \mathit{W_{f}}\:=\:\int_{0}^{\psi_{\mathrm{1}}}\mathit{i\:d\psi }\cdot \cdot \cdot (6)}$$
因此,公式 (6) 表明,储存在磁场中的能量等于电磁系统的 ($\psi -i$) 曲线(即磁化曲线)与磁通链 ($\psi$) 轴之间的面积,如图 2 所示。
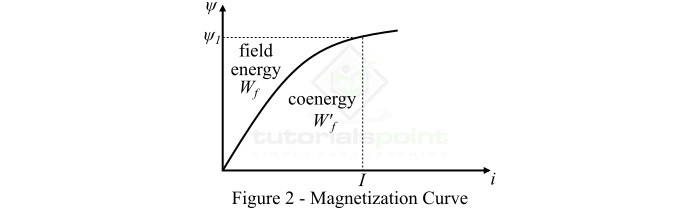
对于线性电磁系统,储存在磁场中的能量由下式给出:
$$\mathrm{\mathit{W_{f}}\:=\:\int_{0}^{\mathit{\psi _{\mathrm{1}}}}\mathit{id\psi }\:=\:\int_{0}^{\psi_{\mathrm{1}} }\frac{\psi }{\mathit{L}}\mathit{d\psi }}$$
其中,$\psi\:=\:\mathit{N\phi }\:=\:\mathit{Li}$,*L* 是线圈的自感。
$$\mathrm{\therefore \mathit{W_{f}}\:=\:\frac{\psi ^{\mathrm{2}}}{2\mathit{L}}\:=\:\frac{1}{2}\mathit{Li^{\mathrm{2}}}\cdot \cdot \cdot (7)}$$
余能的概念
余能是一个虚构的概念,用于推导电磁系统中产生的转矩表达式。因此,余能在系统中没有物理意义。
基本上,余能是 $\psi -i$ 曲线与电流轴之间的面积,表示为 $\mathit{W_{f}^{'}}$,如上图 2 所示。
在数学上,余能由下式给出:
$$\mathrm{\mathit{W_{f}^{'}}\:=\:\int_{0}^{i}\psi \mathit{di}\:=\:\int_{0}^{i}\mathit{Li\:di}}$$
$$\mathrm{\Rightarrow \mathit{W_{f}^{'}}\:=\:\frac{1}{2}\mathit{Li^{\mathrm{2}}}\cdot \cdot \cdot (8)}$$
从公式 (7) 和 (8) 可以看出,对于线性磁系统,储存在磁场中的能量和余能是相等的。
单激发和双激发系统
励磁是指向机电能量转换装置(例如电动机)提供电能输入。励磁在电机中产生工作磁场。有些电机需要单一的电能输入,而有些电机需要两个电能输入。
因此,根据机电能量转换系统的电能输入数量,它们可以分为两种类型:
单激发系统
双激发系统
单激发系统
顾名思义,单激发系统只有一个通电线圈来在机器或任何其他机电能量转换装置中产生工作磁场。因此,单激发系统只需要一个电能输入。
单激发系统由绕在磁芯上的线圈组成,并连接到电压源,以便产生磁场。由于这个磁场,由铁磁材料制成的转子(或运动部分)会受到一个力矩,该力矩将其移动到磁场更强的区域,即作用在转子上的力矩试图将其定位,使其在磁通路径中显示最小的磁阻。磁阻取决于转子角度。这个力矩称为磁阻转矩或凸极转矩,因为它是由转子的凸极引起的。
单激发系统的分析
我们做了以下假设来分析单激发系统:
对于任何转子位置,磁通链 ($\psi$) 和电流 ($\mathit{i}$) 之间的关系是线性的。
线圈的漏磁通可忽略不计,这意味着所有磁通都流经主磁路。
忽略磁滞损耗和涡流损耗。
所有电场都被忽略,磁场占主导地位。
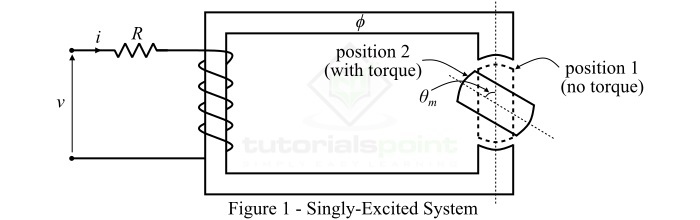
考虑如图 1 所示的单激发系统。如果 *R* 是线圈电路的电阻,则通过应用 KVL,我们可以将电压方程写成:
$$\mathrm{\mathit{v\:=\:iR\:+\:\frac{\mathit{d\psi }}{\mathit{dt}}}\cdot \cdot \cdot (1)}$$
将公式 (1) 乘以电流 $\mathit{i}$,我们得到:
$$\mathrm{\mathit{vi\:=\:i^{\mathrm{2}}R\:+\mathit{i}\:\frac{\mathit{d\psi }}{\mathit{dt}}}\cdot \cdot \cdot (2)}$$
我们假设系统的初始条件为零,并在两边对公式 (2) 关于时间积分,我们得到:
$$\mathrm{\int_{0}^{\mathit{T}}\mathit{vi\:dt}\:=\:\int_{0}^{\mathit{T}}\left ( i^{\mathrm{2}}\mathit{R}\:+\mathit{i}\:\frac{\mathit{d\psi }}{\mathit{dt}} \right )\mathit{dt}}$$
$$\mathrm{\Rightarrow\int_{0}^{\mathit{T}}\mathit{vi\:dt}\:=\:\int_{0}^{\mathit{T}}\mathit{i^{\mathrm{2}}R\:dt}\:+\:\int_{0}^{\psi }\mathit{i\:d\psi }\cdot \cdot \cdot (3)}$$
公式 3 给出了单激发系统的总电能输入,它等于两部分,即:
第一部分是电损耗 ($\mathit{W_{el}}$)。
第二部分是有用电能,它是磁场能量 ($\mathit{W_{f}}$) 和输出机械能 ($\mathit{W_{m}}$) 之和。
因此,我们可以用符号表示公式 3 为:
$$\mathrm{\mathit{W_{in}}\:=\:\mathit{W_{el}}\:=\:\left (\mathit{W_{f}} \:+\:\mathit{W_{m}} \right )}\cdot \cdot \cdot (4)$$
单激励系统的磁场储存能量由下式给出:
$$ \mathrm{\mathit{W_{f}}\:=\: \int_{0}^{\psi }\mathit{i\:d\psi }\:=\:\int_{0}^{\psi }\frac{\psi }{\mathit{L}}\mathit{d\psi }\:=\:\frac{\psi ^{\mathrm{2}}}{2\mathit{L}}\cdot \cdot \cdot (5)} $$
对于转子运动,其中转子角度为$\mathit{\theta _{m}}$,单激励系统中产生的电磁转矩由下式给出:
$$ \mathrm{\mathit{\tau _{e}}\:=\:\frac{\mathit{i^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{\partial L}}{\mathit{\partial \theta _{m}}}\cdot \cdot \cdot (6)} $$
单激励系统最常见的例子包括感应电机、PMMC仪表等。
双激励系统
具有两个独立线圈来产生磁场的电磁系统被称为双激励系统。因此,双激励系统需要两个独立的电输入。
双激励系统的分析
双激励系统由两个主要部分组成,即定子和转子,如图2所示。这里,定子绕组具有电阻R1,转子绕组具有电阻R2。因此,有两个独立的绕组,由两个独立的电压源激励。
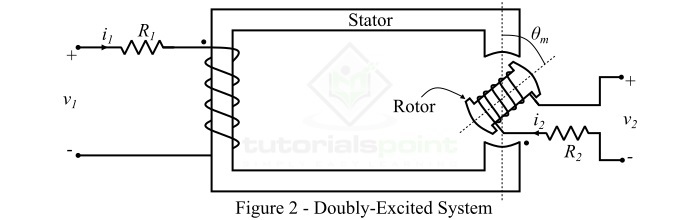
为了分析双激励系统,做出以下假设:
对于任何转子位置,磁链 ($\psi$) 和电流之间的关系都是线性的。
忽略滞后和涡流损耗。
线圈的漏磁可忽略不计。
忽略电场,磁场占主导地位。
两个绕组的磁通链由下式给出:
$$ \mathrm{\psi _{\mathrm{1}}\:=\:\mathit{L_{\mathrm{1}}i_{\mathrm{1}}}\:+\:\mathit{Mi_{\mathrm{2}}}}\cdot \cdot \cdot (7) $$
$$ \mathrm{\psi _{\mathrm{2}}\:=\:\mathit{L_{\mathrm{2}}i_{\mathrm{2}}}\:+\:\mathit{Mi_{\mathrm{2}}}}\cdot \cdot \cdot (8) $$
其中,M 是两个绕组之间的互感。
应用基尔霍夫电压定律,我们可以写出两个线圈的瞬时电压方程:
$$ \mathrm{\mathit{v}_{\mathrm{1}}\:=\:\mathit{i_{\mathrm{1}}R_{\mathrm{1}}}\:+\:\frac{\mathit{d\psi _{\mathrm{1}}}}{\mathit{dt}}}\cdot \cdot \cdot (9) $$
$$ \mathrm{\mathit{v}_{\mathrm{2}}\:=\:\mathit{i_{\mathrm{2}}R_{\mathrm{2}}}\:+\:\frac{\mathit{d\psi _{\mathrm{2}}}}{\mathit{dt}}}\cdot \cdot \cdot (10) $$
在双激励系统中,磁场储存能量由下式给出:
$$ \mathrm{\mathit{W_{f}}\:=\:\frac{1}{2}\mathit{L_{\mathrm{1}}i_{\mathrm{1}}^{\mathrm{2}}}\:+\:\frac{1}{2}\mathit{L_{\mathrm{2}}i_{\mathrm{2}}^{\mathrm{2}}}\:+\:\mathit{Mi_{\mathrm{1}}i_{\mathrm{2}}}\cdot \cdot \cdot (11)} $$
并且,双激励系统中产生的电磁转矩由下式给出:
$$ \mathrm{\mathit{\tau _{e}}\:=\:\frac{\mathit{i_{\mathrm{1}}^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{dL_{\mathrm{1}}}}{\mathit{d\theta _{m}}}\:+\:\frac{\mathit{i_{\mathrm{2}}^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{dL_{\mathrm{2}}}}{\mathit{d\theta _{m}}}\:+\:\mathit{i_{\mathrm{1}}i_{\mathrm{2}}}\frac{\mathit{dM}}{\mathit{d\theta _{m}}}\cdot \cdot \cdot (12)} $$
在公式(12)中,前两项是磁阻转矩,最后一项是由于两个磁场的相互作用而产生的同轴转矩。
双激励系统的实际例子包括同步电机、测速机、他励直流电机等。
旋转电机
几乎所有电机都具有几个相似的特性和功能。以下讨论将解释旋转电机的基本共同特性。其中,旋转电机是指具有一个运动(旋转)部分(称为转子)的电机。旋转电机的常见例子包括电动机和发电机。
在旋转电机中,产生的转矩可以根据瞬时磁通模式来考虑。根据这一概念,当净磁场具有不对称性或畸变时,会在电机中产生转矩。
在任何旋转电机中,机械力(转矩)都是由于以下两种磁场效应产生的:
磁力线的对准
磁场与载流导体之间的相互作用
在实际电机中,磁场是通过励磁线圈系统产生的。这是因为这种磁场产生方法相对通用且经济。
旋转电机的基本结构
所有旋转电机的基本结构和构造都是相似的。典型的旋转电机由两个主要部分组成,即:
定子
转子
定子和转子之间由气隙隔开。顾名思义,定子是电机的静止(不可移动)部分。通常,定子是电机的外部框架。转子是电机的旋转(可移动)部分。定子和转子都是使用叠片铁磁材料制成的,以减少磁通路径中的磁阻。
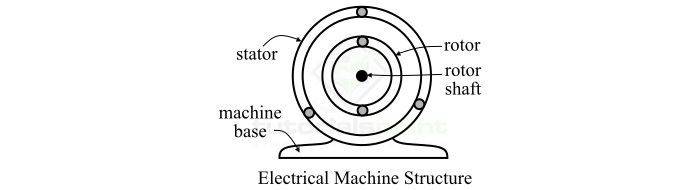
所有旋转电机都包含两个绕组,一个放置在定子上,另一个放置在转子上。在其中感应电压的电机绕组被称为电枢绕组。用于在电机中产生主要工作磁通的绕组被称为励磁绕组。有时,使用永磁体代替励磁绕组来产生主要的磁通。
旋转磁场
由对称布置并供以多相电流的绕组(线圈)系统产生的在空间中旋转的合成磁场称为旋转磁场 (RMF)。
旋转磁场是这样的,它的磁极不会保持在固定位置,而是不断地改变其位置。磁场旋转的速度称为同步速度,用 NS 表示。同步速度的数学表达式为:
$$ \mathrm{\mathit{N_{s}}\:=\:\frac{120\mathit{f}}{\mathit{P}}} $$
其中,f 是以 Hz 为单位的电源频率,P 是极数。它以RPM(每分钟转数)为单位测量。
电机转矩
转矩定义为力的旋转运动。转矩是旋转电机转子的主要因素。在机电设备中,产生两种类型的转矩:
电磁转矩
磁阻转矩
电磁转矩
电磁转矩是由两个可能彼此相对移动的线圈中的电流产生的磁场的相互作用产生的。在旋转电机中,在正常运行条件下,存在两个磁场——一个来自定子电路的磁场,另一个来自转子电路的磁场。这两个磁场之间的相互作用在电机中产生转矩。这个转矩称为电磁转矩。电磁转矩也称为感应转矩。
磁阻转矩
当由铁磁材料制成的物体置于外部磁场中时,会受到力(转矩)的作用,使物体与外部磁场对齐,这称为磁阻转矩。
磁阻转矩的产生是因为外部磁场在铁磁物体中感应出内部磁场,并且两个磁场的相互作用产生转矩,使物体移动以与外部磁场对齐。由于磁阻转矩作用于物体,试图使物体处于磁通的最小磁阻(或凸极性)位置。因此,磁阻转矩也称为对准转矩或凸极转矩。
法拉第电磁感应定律
当变化的磁场与导体或线圈连接时,在导体或线圈中会产生电动势,这种现象称为电磁感应。电磁感应是设计电机最基本的概念。
英国科学家迈克尔·法拉第进行了几次实验来演示电磁感应现象。他将所有实验的结果总结为两条定律,俗称法拉第电磁感应定律。
法拉第第一定律
法拉第电磁感应第一定律提供了关于在导体或线圈中感应电动势的条件的信息。第一定律指出:
当与导体或线圈连接的磁通发生变化时,在导体或线圈中就会感应出电动势。
因此,在导体或线圈中感应电动势的基本需求是与导体或线圈连接的磁通量的变化。
法拉第第二定律
法拉第电磁感应第二定律给出了导体或线圈中感应电动势的大小,可以表述如下:
导体或线圈中感应电动势的大小与磁通链随时间的变化率成正比。
解释
假设一个线圈有 N 个匝数,并且与线圈连接的磁通量在 t 秒内从 $\mathit{\phi _{\mathrm{1}}}$ 韦伯变为 $\mathit{\phi _{\mathrm{2}}}$ 韦伯。现在,线圈的磁通链 ($\mathit{\psi }$) 是磁通量和线圈匝数的乘积。因此,
$$ \mathrm{\mathrm{初始磁通链,}\mathit{\psi _{\mathrm{1}}}\:=\:\mathit{N\phi _{\mathrm{1}}}} $$
$$ \mathrm{\mathrm{最终磁通链,}\mathit{\psi _{\mathrm{2}}}\:=\:\mathit{N\phi _{\mathrm{2}}}} $$
根据法拉第电磁感应定律,
$$ \mathrm{\mathrm{感应电动势,}\mathit{e}\propto \frac{\mathit{N\phi _{\mathrm{2}}}-\mathit{N\phi} _{\mathrm{1}}}{\mathit{t}}\cdot \cdot \cdot (1)} $$
$$ \mathrm{\Rightarrow \mathit{e}\:=\:\mathit{k}\left ( \frac{\mathit{N\phi _{\mathrm{2}}}-\mathit{N\phi} _{\mathrm{1}}}{\mathit{t}} \right )} $$
其中,k 是比例常数,在 SI 单位中其值为 1。
因此,线圈中感应的电动势由下式给出:
$$ \mathrm{\mathit{e}\:=\:\frac{\mathit{N\phi _{\mathrm{2}}}-\mathit{N\phi} _{\mathrm{1}}}{\mathit{t}}\cdot \cdot \cdot (2)} $$
微分形式为:
$$ \mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\cdot \cdot \cdot (3)} $$
感应电动势的方向总是使得它倾向于建立一个电流,该电流产生的磁通量会阻碍引起感应电动势的磁通量变化。因此,线圈中感应电动势的大小和方向应写为:
$$ \mathrm{ \mathit{e}\:=\:\mathit{-N}\frac{\mathit{d\phi }}{\mathit{dt}}\cdot \cdot \cdot (4)} $$
其中,负号 (-) 表示感应电动势的方向使得它阻碍产生它的原因,即磁通量的变化,这个说法被称为楞次定律。公式 (4) 是楞次定律的数学表示。
感应电动势的概念
根据电磁感应原理,当与导体或线圈连接的磁通量发生变化时,在导体或线圈中就会感应出电动势。在实践中,采用以下两种方法来改变磁通链:
方法 1 - 导体在静止磁场中运动
我们可以使导体或线圈在静止磁场中运动,使得与导体或线圈连接的磁通量的大小发生变化。因此,在导体中会感应出电动势。这种感应电动势称为动态感应电动势。之所以这样称呼,是因为它是感应在运动的导体中的电动势。动态感应电动势的例子是交流发电机和直流发电机中产生的电动势。
方法 2 - 静止导体置于变化的磁场中
当静止导体或线圈置于运动的或变化的磁场中时,在导体或线圈中就会感应出电动势。以这种方式感应的电动势称为静态感应电动势。之所以这样称呼,是因为电动势是感应在静止的导体中的。变压器中感应的电动势是静态感应电动势的一个例子。
因此,从上面的讨论可以看出,感应电动势可以分为两大类:
动态感应电动势
静态感应电动势
动态感应电动势
如上节所述,动态感应电动势是在置于静止磁场中的运动导体或线圈中感应的电动势。动态感应电动势的表达式可以如下推导:
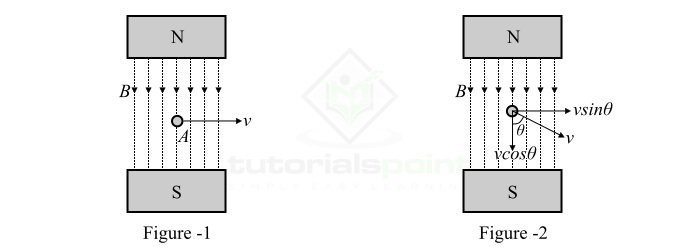
考虑一根长度为l米、位于磁通密度为B Wb/m2的均匀磁场中的单根导体,如图1所示。该导体以v m/s的速度垂直于磁场运动。
现在,如果导体在dt秒内移动一小段距离dx,则导体扫过的面积为:
$$\mathrm{\mathit{A\:=\:l\times dx\:}\mathrm{m^{\mathrm{2}}}}$$
因此,导体切割的磁通量为:
$$\mathrm{\mathit{d\phi }\:=\:\mathrm{磁通密度\times 扫过面积}}$$
$$\mathrm{\Rightarrow \mathit{d\phi }\:=\:\mathit{B\times l\times dx}\:\mathrm{Wb}}$$
根据法拉第电磁感应定律,导体中感应的电动势为:
$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\:=\:\mathit{N}\frac{\mathit{Bldx}}{\mathit{dt}}}$$
由于我们只考虑了一根导体,因此N = 1。
$$\mathrm{\mathit{e}\:=\:\mathit{Blv}\:\mathrm{伏特}\cdot \cdot \cdot (1)}$$
其中,v = dx/dt,为导体在磁场中的速度。
如果导体在磁场中存在角运动,并且导体相对于磁场以θ角移动,如图2所示。则导体穿过磁场的速度等于“vsinθ”。因此,感应电动势为:
$$\mathrm{\mathit{e}\:=\:\mathit{B\:l\:v}\:\mathrm{sin\mathit{\theta }}\:\mathrm{伏特}\cdot \cdot \cdot (2)}$$
静态感应电动势
当静止导体置于变化的磁场中时,导体中感应的电动势称为**静电感应电动势**。静电感应电动势进一步分为以下两种类型:
自感电动势
互感电动势
自感电动势
当由于导体或线圈自身磁通链路的改变而在导体或线圈中感应出电动势时,它被称为**自感电动势**。
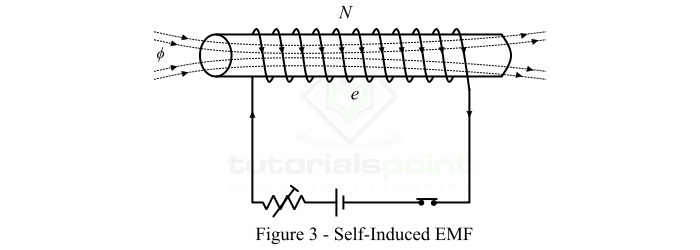
考虑一个如图3所示的N匝线圈。流过线圈的电流在线圈中建立磁场。如果线圈中的电流发生变化,则与线圈相关的磁通量也会发生变化。根据法拉第电磁感应定律,这个变化的磁场在线圈中感应出电动势。这种电动势称为自感电动势,自感电动势的大小由下式给出:
$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
互感电动势
由于相邻线圈变化的磁场在线圈中感应出的电动势称为**互感电动势**。
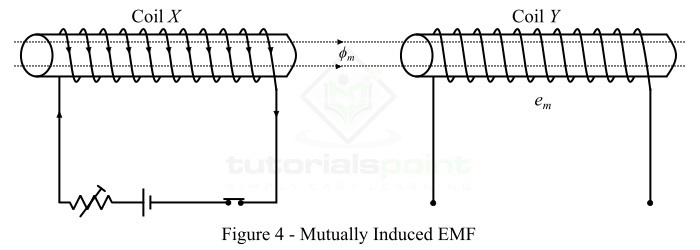
考虑两个线圈X和Y彼此相邻放置,如图4所示。这里,线圈X产生的磁通量的一部分与线圈Y相连。线圈X的这种对线圈X和Y都共有的磁通量称为**互感磁通量($\mathit{\phi _{m}}$)**。
如果线圈X中的电流发生变化,则互感磁通量也会发生变化,因此在线圈中感应出电动势。其中,在线圈X中感应的电动势称为自感电动势,在线圈Y中感应的电动势称为**互感电动势**。
根据法拉第定律,互感电动势的大小由下式给出:
$$\mathrm{\mathit{e_{m}}\:=\:\mathit{N_{Y}}\frac{\mathit{d\phi _{m}}}{\mathit{dt}}}$$
其中,$\mathit{N_{Y}}$是线圈Y的匝数,$\frac{\mathit{d\phi _{m}}}{\mathit{dt}}$是互感磁通量的变化率。
弗莱明左手定则和右手定则
所有电机都基于**电磁感应原理**工作。根据该原理,如果导体和磁场之间存在相对运动,则会在导体中感应出电动势。另一方面,如果载流导体置于磁场中,则导体会受到力的作用。出于实际和分析的目的,确定导体中感应电动势的方向和作用在导体上的力的方向非常重要。**弗莱明右手定则**用于此目的。
英国电气工程师和物理学家**约翰·安布罗斯·弗莱明**在19世纪后期提出了两条规则,用于确定置于磁场中的载流导体上感应电动势的方向和作用力。这些规则俗称**弗莱明左手定则**和**弗莱明右手定则**。
基本上,左手定则和右手定则都显示了磁场、力和电流之间的关系。
弗莱明左手定则用于确定载流导体在磁场中受到的力的方向,因此主要适用于电动机。而弗莱明右手定则用于确定相对于磁场移动的导体中感应电动势的方向,因此主要适用于发电机。
弗莱明左手定则
**弗莱明左手定则**特别适用于寻找载流导体在磁场中受力的方向,其陈述如下:
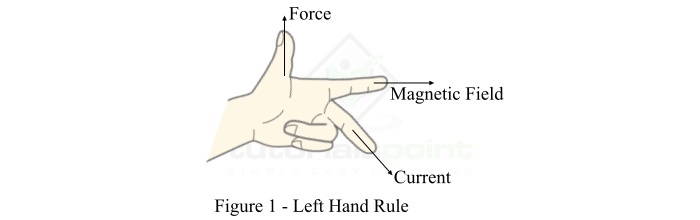
伸出你左手的食指、中指和拇指,使它们相互垂直(如图1所示)。如果食指指向磁场方向,中指指向导体中电流的方向,则拇指将指向导体上力的方向。
在实践中,弗莱明左手定则用于确定电动机中导体运动的方向。
弗莱明右手定则
**弗莱明右手定则**特别适用于确定当导体和磁场之间存在相对运动时,导体中感应电动势的方向以及电流的方向。弗莱明右手定则可以表述如下:
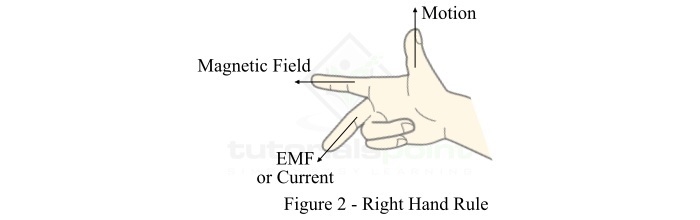
伸出你右手的食指、中指和拇指,使它们相互垂直(如图2所示)。如果食指指向磁场方向,拇指指向导体运动的方向,则中指将指向感应电动势或电流的方向。
在实践中,弗莱明右手定则用于确定发电机中感应电动势和电流的方向。
弗莱明左手定则和右手定则的比较
下表简要比较了弗莱明左手定则和右手定则:
| 参数 | 弗莱明左手定则 | 弗莱明右手定则 |
|---|---|---|
| 用途 | 弗莱明左手定则用于确定载流导体在磁场中受力的方向。 | 弗莱明右手定则用于确定导体中感应电动势或电流的方向。 |
| 应用 | 弗莱明左手定则主要适用于电动机。 | 弗莱明右手定则适用于发电机。 |
电力变压器
在电力和电子系统中,**电力变压器**是最有用的电力设备之一。电力变压器可以升高或降低交流电压或电流的大小。这是交流电比直流电广泛应用的主要原因。变压器没有任何移动部件。因此,它的效率非常高,可达99%,结构非常坚固耐用。
电力变压器
**变压器**或**电力变压器**是一种静态交流电力设备,它可以在不改变电源频率的情况下改变交流电压或交流电流的电平。
典型的变压器由两个绕组组成,即**初级绕组**和**次级绕组**。这两个绕组通过一个公共磁路相互连接,用于在它们之间传输电能。
变压器工作原理
变压器的工作原理是基于**互感原理**,该原理指出,当一个线圈变化的磁场与另一个线圈相连时,在第二个线圈中会感应出电动势。
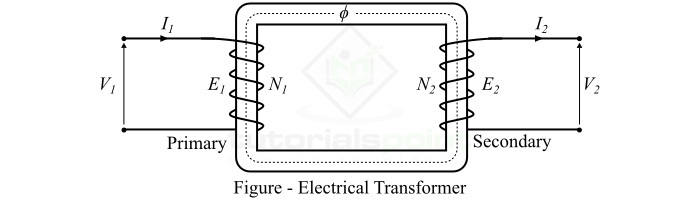
当将交流电压V1施加到初级绕组时,交流电流流过它并产生交流磁通。这种变化的磁通流过变压器的铁芯并与次级绕组相连。根据法拉第电磁感应定律,由于初级绕组变化磁通的连接,在次级绕组中感应出电动势E2。如果通过连接负载来闭合次级绕组电路,则次级绕组中的感应电动势E2会导致次级电流I2流过负载。
虽然初级绕组的变化磁通也与初级绕组本身相连。因此,由于其自身的电感效应,在初级绕组中感应出电动势E1。E1和E2的值可以用以下公式给出:
$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:-\mathit{N_{\mathrm{1}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:-\mathit{N_{\mathrm{2}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
其中N1和N2分别是初级绕组和次级绕组的匝数。
取E2和E1的比率,我们得到:
$$\mathrm{\frac{\mathit{E_{\mathrm{2}}}}{\mathit{E_{\mathrm{1}}}}\:=\:\frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}}}$$
这个表达式称为变压器的**变压比**。变压比取决于初级和次级绕组的匝数。这意味着输出电压的大小取决于初级和次级绕组的相对匝数。
如果N2 > N1,则E2 > E1,即变压器的输出电压大于输入电压,这种变压器称为**升压变压器**。另一方面,如果N1 > N2,则E1 > E2,即输出电压小于输入电压,这种变压器称为**降压变压器**。
从变压器的电路图中,我们可以看到初级和次级之间没有电气连接,而是通过磁场连接。因此,变压器使我们能够将交流电能以磁的方式从一个电路转移到另一个电路,同时改变电压和电流水平。
要点
注意以下关于变压器的要点:
变压器的运行基于电磁感应原理。
变压器不改变频率,即输入电源和输出电源的频率保持不变。
变压器是一种静态电力设备,这意味着它没有任何运动部件。因此,它具有很高的效率。
变压器不能与直流电一起工作,因为它是一种电磁感应设备。
原边和副边绕组之间没有直接的电气连接。交流电通过磁通量从原边传输到副边。
变压器的构造
变压器主要由三个部分组成:原边绕组、副边绕组和铁心。原边绕组用于输入电源,副边绕组用于输出。铁心用于将磁通量限制在一定的路径内。
我们设计的变压器尽可能接近理想变压器的特性。在实践中,我们为变压器的构造采用了以下设计特点:
变压器的铁心由高品质硅钢制成,具有高磁导率和低磁滞损耗。
铁心采用叠片结构以最大限度地减少涡流损耗。
通常更有效的方法是在一个铁芯柱上绕制原边和副边绕组的一半,而不是将原边绕组放在一个铁芯柱上,副边绕组放在另一个铁芯柱上。这样做可以确保两个绕组之间紧密的磁耦合,从而大大减少漏磁通。
绕组电阻R1和R2尽可能减小,以使I2R损耗和温升降至最低,并确保更高的效率。
变压器结构
变压器可以通过以下两种方式构造:
核心式变压器结构
壳式变压器结构
核心式变压器结构
在核心式变压器的结构中,铁心有两个垂直的支柱(称为铁芯柱)和两个水平部分(称为轭)。原边绕组的一半和副边绕组的一半分别绕在每个铁芯柱上,如图1所示。
这种绕组布置最大限度地减少了漏磁通。在实践中,低压绕组(可以是原边或副边)靠近铁心放置,高压绕组绕在低压绕组周围。这大大减少了绝缘材料的需求。
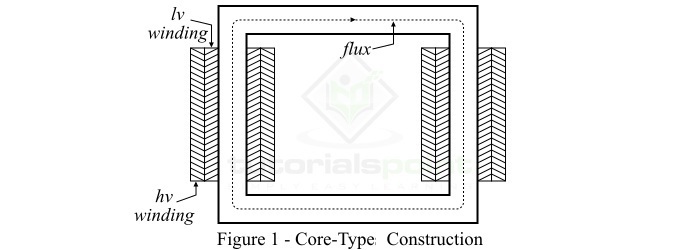
核心式变压器结构的主要优点是易于拆卸维修。核心式结构最适合高压大功率变压器,因为在核心式结构中,自然冷却效率更高。
壳式变压器结构
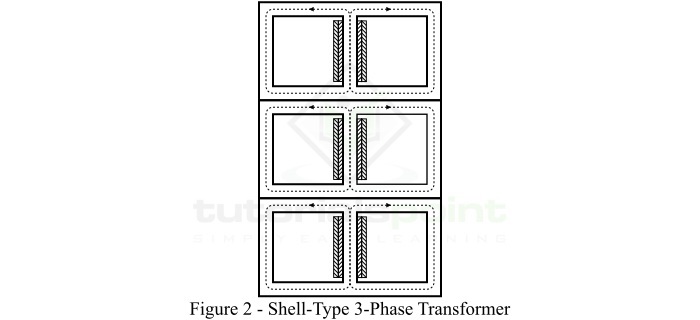
在壳式变压器的结构中,原边和副边绕组都绕在中心铁芯柱上,而两个外侧铁芯柱构成低磁阻的磁通路径,如图2所示。
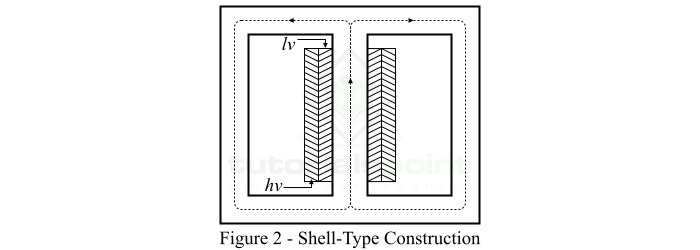
在这种情况下,每个绕组都细分为几段,低压(lv)绕组段和高压(hv)绕组段交替排列成三明治状。因此,这种类型的绕组也称为三明治绕组或叠片绕组。
壳式变压器结构提供了更好的机械支撑,可以抵抗载流绕组之间的电磁力。此外,这种变压器结构为磁通提供了更短的路径,因此需要较小的励磁电流。由于绕组嵌入,壳式结构的自然冷却效果较差,因此更适用于低压变压器。
变压器的电动势方程
对于电力变压器,电动势方程是用于求解变压器绕组中感应电动势大小的数学表达式。
考虑图中所示的变压器。如果N1和N2是原边和副边绕组的匝数。当我们将频率为f的交流电压V1施加到原边绕组时,原边绕组在铁心中产生交变磁通量$\phi$。
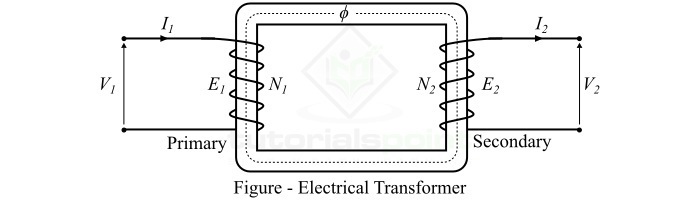
如果我们假设正弦交流电压,则磁通量可以表示为:
$$\mathrm{\mathit{\phi }\:=\:\phi _{m}\:\mathrm{sin}\:\mathit{\omega t}\:\cdot \cdot \cdot (1)}$$
现在,根据电磁感应原理,原边绕组中感应电动势e1的瞬时值由下式给出:
$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\frac{\mathit{d}}{\mathit{dt}}\left ( \phi _{m}\: \mathrm{sin}\:\mathit{\omega t}\right )}$$
$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\:\mathit{\omega \phi \:cos\:\omega t}}$$
$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:-\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m} \:cos\:\omega t}}$$
其中:
$$\mathrm{\mathit{\omega \:=\:\mathrm{2}\pi f}}$$
$$\mathrm{\because -\mathit{cos\:\omega t}\:=\:\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )}$$
因此,
$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m}\:\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )}}\:\cdot \cdot \cdot (2)$$
方程(2)可以写成:
$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathit{E_{m_{\mathrm{1}}}}\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )\:\cdot \cdot \cdot (3)}$$
其中,$\mathit{E_{m_{\mathrm{1}}}}$是感应电动势$\mathit{e_{\mathrm{1}}}$的最大值。
$$\mathrm{\mathit{E_{\mathrm{m1}}}\:=\:\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m}}}$$
现在,对于正弦电源,原边绕组电动势的有效值$\mathit{E_{\mathrm{1}}}$由下式给出:
$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:\frac{\mathit{E_{m\mathrm{1}}}}{\sqrt{2}}\:=\:\frac{2\mathit{\pi fN_{\mathrm{1}}}\phi_{m}}{\sqrt{2}}}$$
$$\mathrm{\therefore\mathit{E_{\mathrm{1}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{1}}}\:\cdot \cdot \cdot (4)}$$
类似地,副边绕组电动势的有效值E2为:
$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{2}}}\:\cdot \cdot \cdot (5)}$$
一般来说,
$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}N}\:\cdot \cdot \cdot (6)}$$
方程(6)称为变压器的电动势方程。
对于给定的变压器,如果我们将电动势方程除以电源频率,我们得到:
$$\mathrm{\frac{\mathit{E}}{\mathit{f}}\:=\:4.44\:\phi _{m}\mathit{N}\:=\:\mathrm{Constant}}$$
这意味着每单位频率的感应电动势是恒定的,但在给定变压器的原边和副边并不相同。
此外,从方程(4)和(5),我们有:
$$\mathrm{\frac{\mathit{E_{\mathrm{1}}}}{\mathit{E_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}\:or\:\frac{\mathit{E_{\mathrm{1}}}}{\mathit{N_{\mathrm{1}}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{N_{\mathrm{2}}}}}$$
因此,在变压器中,原边绕组每匝的感应电动势等于副边绕组每匝的感应电动势。
数值例子
一台单相3300/240 V,50 Hz变压器,铁心中的最大磁通量为0.0315 Wb。计算原边和副边绕组的匝数。
解答
已知数据:
$$\mathrm{\mathit{E_{\mathrm{1}}\:=\:\mathrm{3300}\:\mathrm{V}\:\mathrm{and}\:\mathit{E_{\mathrm{2}}\:=\:\mathrm{240}\:V}}}$$
$$\mathrm{\mathit{f}\:=\:50\:Hz;\:\phi _{m}\:=\:0.0315\:Wb}$$
变压器的电动势方程为:
$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}N}}$$
因此,对于原边绕组:
$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:\frac{\mathit{E_{\mathrm{1}}}}{4.44\:\mathit{f\phi _{m}}}\:=\:\frac{3300}{4.44\times 50\times 0.0315}}$$
$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:471.9\:=\:472}$$
同样,对于副边绕组:
$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{4.44\:\mathit{f\phi _{m}}}\:=\:\frac{240}{4.44\times 50\times 0.0315}}$$
$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:34.32\:=\:35}$$
绕组不可能有部分匝数。因此,匝数必须是整数。
变压比和电压变换比
如前章所述,变压器的电动势方程为:
$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}\:N}}$$
对于原边绕组:
$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:4.44\:\mathit{f\phi _{m}\:N_{\mathrm{1}}}\:\cdot \cdot \cdot (1)}$$
对于副边绕组:
$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:4.44\:\mathit{f\phi _{m}\:N_{\mathrm{2}}}\:\cdot \cdot \cdot (2)}$$
变压器的变压比
从方程(1)和(2),我们有:
$$\mathrm{\frac{\mathit{E_{\mathrm{1}}}}{\mathit{E_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}\:=\mathrm{a}\:\:\cdot \cdot \cdot (3)}$$
常数“a”称为变压器的变压比。它可以定义如下:
变压器原边绕组匝数与副边绕组匝数的比值称为变压比。
变压器的电压变比
变压器的输出电压与输入电压的比值称为电压变比,即:
$$\mathrm{\mathrm{变压比}\:=\:\frac{输出电压}{输入电压}}$$
因此,如果V1是变压器的输入电压,V2是输出电压,则其变压比由下式给出:
$$\mathrm{\mathrm{变压比}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{V_{\mathrm{1}}}}\:\cdot \cdot \cdot (4)}$$
对于理想变压器,V1 = E1 和 V2 = E2,则
$$\mathrm{\mathrm{变压比}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{V_{\mathrm{1}}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{E_{\mathrm{1}}}}\:=\:\:\frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}}\:=\:\frac{1}{a}\cdot \cdot \cdot (5)}$$
然而,在实际变压器中,由于绕组电阻的存在,V1和E1之间以及V2和E2之间存在微小差异。尽管这种差异非常小,但在分析目的中,我们取V1 = E1和V2 = E2。
数值例子(1)
一个变压器,原边匝数为1000匝,副边匝数为400匝,由220 V交流电源供电。计算副边电压和每匝电压。
解答
已知数据:
$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:1000\:\mathrm{and}\:\mathit{N_{\mathrm{2}}}\:=\:400}$$
$$\mathrm{\mathit{V_{\mathrm{1}}}\:=\:220\:V}$$
变压器的变压比为:
$$\mathrm{\frac{\mathit{V_{\mathrm{1}}}}{\mathit{V_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}}$$
$$\mathrm{\Rightarrow \mathit{V_{\mathrm{2}}}\:=\:\mathit{V_{\mathrm{1}}}\times \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}}\:=\:220\times \frac{400}{1000}}$$
$$\mathrm{\therefore\mathit{V_{\mathrm{2}}}\:=\:88\:\mathrm{Volts}}$$
每匝电压由下式给出:
$$\mathrm{\mathrm{原边绕组}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{\mathit{N_{\mathrm{1}}}}\:=\:\frac{200}{1000}\:=\:0.22\:\mathrm{Volts}}$$
$$\mathrm{\mathrm{副边绕组}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{N_{\mathrm{2}}}}\:=\:\frac{88}{400}\:=\:0.22\:\mathrm{Volts}}$$
因此,从这个例子可以看出,变压器的每匝电压在原边和副边绕组上保持相同。
数值例子(2)
一个输出电压为2200 V的变压器,由220 V电源供电。如果副边绕组有2000匝,则计算原边绕组的匝数。
解答
已知数据:
$$\mathrm{\mathit{V_{\mathrm{1}}}\:=\:200\:\mathit{V}\:\mathrm{and}\:\mathit{V_{\mathrm{2}}}\:=\:2200\:\mathit{V}}$$
$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:2000\:\mathrm{turns}}$$
变压器的变压比为:
$$\mathrm{\frac{\mathit{V_{\mathrm{1}}}}{\mathit{V_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}}$$
$$\mathrm{\Rightarrow {\mathit{N_{\mathrm{1}}}}\:=\:\mathit{N_{\mathrm{2}}}\:\times \:\frac{\mathit{V_{\mathrm{1}}}}{\mathit{V_{\mathrm{2}}}}\:=\:\mathrm{2000}\:\times \:\frac{220}{2200}\:=\:\mathrm{200\:turns}}$$
理想变压器和实际变压器
理想变压器
理想变压器是变压器的理想模型,具有以下特性:
原边和副边绕组的电阻可以忽略不计(或为零)。
没有漏磁通,即所有磁通都流经变压器的铁心。
铁心的磁导率无限大,这意味着建立铁心磁通所需的磁动势可以忽略不计。
没有由于绕组电阻、磁滞和涡流引起的损耗。因此,其效率为100%。
理想变压器的运行
我们可以分析理想变压器在空载或负载下的运行情况,这将在以下部分讨论。
理想变压器空载运行
考虑一个空载运行的理想变压器,即其副边绕组是开路的,如图1所示。原边绕组是一个纯电感线圈。
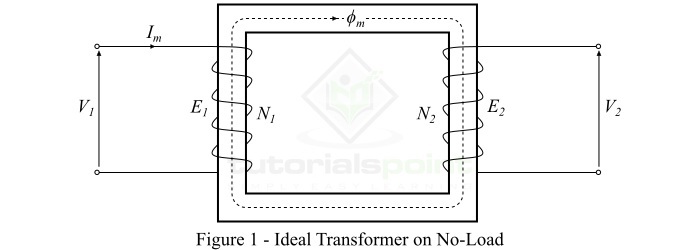
当将交流电压$\mathit{V_{\mathrm{1}}}$施加到原边绕组时,它会吸收很小的励磁电流$\mathit{I_{\mathit{m}}}$以在铁心中建立磁通,该电流滞后于施加电压90°。励磁电流Im在铁心中产生与之成比例且同相位的交变磁通量$\mathit{\phi_{m}}$。这个交变磁通量($\mathit{\phi_{m}}$)通过磁耦合方式与原边和副边绕组连接,并在原边绕组中感应出电动势$\mathit{E_{\mathrm{1}}}$,并在副边绕组中感应出电动势$\mathit{E_{\mathrm{2}}}$。
原边绕组感应电动势 $\mathit{E_{\mathrm{1}}}$ 等于并与外加电压 $\mathit{V_{\mathrm{1}}}$ 反向(根据 *楞次定律*)。电动势 $\mathit{E_{\mathrm{1}}}$ 和 $\mathit{E_{\mathrm{2}}}$ 滞后于磁通 ($\mathit{\phi_{m}}$) 90°,但是它们的幅值取决于原边和副边绕组的匝数。此外,电动势 $\mathit{E_{\mathrm{1}}}$ 和 $\mathit{E_{\mathrm{2}}}$ 彼此同相,而 $\mathit{E_{\mathrm{1}}}$ 与 $\mathit{V_{\mathrm{1}}}$ 相等且相位差 180°。
理想变压器带负载运行
当负载连接到理想变压器副边绕组的端子时,则称变压器带负载运行,负载电流流过副边绕组和负载。
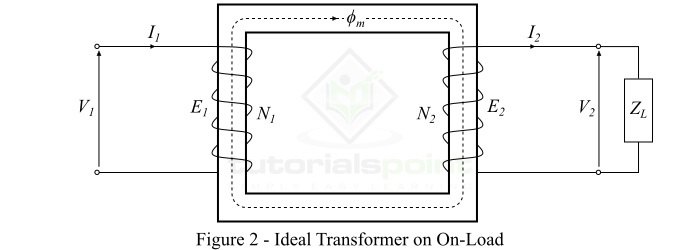
考虑一个阻抗连接在理想变压器副边绕组上的感性负载,如图 2 所示。则副边绕组电动势 $\mathit{E_{\mathrm{2}}}$ 将导致电流 $\mathit{I_{\mathrm{2}}}$ 流过副边绕组和负载,其计算公式为:
$$\mathrm{\mathit{I_{\mathrm{2}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}}$$
其中,对于理想变压器,副边绕组电动势 $\mathit{E_{\mathrm{2}}}$ 等于副边绕组端电压 $\mathit{V_{\mathrm{2}}}$。
由于我们考虑的是感性负载,因此电流 $\mathit{I_{\mathrm{2}}}$ 将滞后于 $\mathit{E_{\mathrm{2}}}$ 或 $\mathit{V_{\mathrm{2}}}$ 一个 $\mathit{\phi_{\mathrm{2}}}$ 角。此外,空载电流 $\mathit{I_{\mathrm{0}}}$ 被忽略,因为变压器是理想的。
流过副边绕组的电流 ($\mathit{I_{\mathrm{2}}}$) 建立一个磁动势 ($\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$),该磁动势产生一个与主磁通 ($\mathit{\phi_{\mathit{m}}}$) 反向的磁通 $\mathit{\phi_{\mathrm{2}}}$。结果,铁芯中的总磁通量与其原始值发生变化,但是,铁芯中的磁通量不应偏离其原始值。因此,为了保持铁芯中的磁通量为其原始值,原边电流必须产生一个磁动势,以抵消副边磁动势 $\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$ 的退磁作用。
因此,原边电流 $\mathit{I_{\mathrm{1}}}$ 必须流动,以便
$$\mathrm{\mathit{I_{\mathrm{1}}}\mathit{N_{\mathrm{1}}}\:=\:\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}}$$
因此,原边绕组必须汲取足够的电流来中和副边电流的退磁作用,以使铁芯中的主磁通保持恒定。因此,当副边电流 ($\mathit{I_{\mathrm{2}}}$) 增加时,原边电流 ($\mathit{I_{\mathrm{1}}}$) 也以相同的方式增加,并保持互磁通 ($\mathit{\phi_{\mathit{m}}}$) 恒定。
在带负载的理想变压器中,副边电流 $\mathit{I_{\mathrm{2}}}$ 滞后于副边端电压 $\mathit{V_{\mathrm{2}}}$ 一个 $\mathit{\phi _{\mathrm{2}}}$ 角。
实际变压器
实际变压器具有以下特性:
原边和副边绕组具有有限的电阻。
存在漏磁通,即并非所有磁通都限制在磁芯内。
磁芯具有有限的磁导率,因此需要相当大的磁动势来在铁芯中建立磁通。
由于绕组电阻、磁滞和涡流,变压器会产生损耗。因此,实际变压器的效率总是小于 100%。
典型的实际变压器的分析模型如图 3 所示。
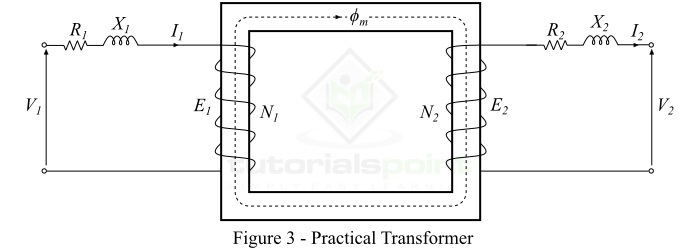
实际变压器的特性
以下是实际变压器的重要特性:
绕组电阻
变压器的绕组通常由铜导体组成。因此,原边和副边绕组都将具有绕组电阻,这会在变压器中产生铜损或 $\mathit{i^{\mathrm{2}} \mathit{R}}$ 损耗。原边绕组电阻 $\mathit{R_{\mathrm{1}}}$ 和副边绕组电阻 $\mathit{R_{\mathrm{2}}}$ 分别与各自的绕组串联,如图 3 所示。
铁损或铁芯损耗
变压器的铁芯经受交变磁通,因此铁芯中会产生涡流损耗和磁滞损耗。磁滞损耗和涡流损耗合称为 **铁损** 或 **铁芯损耗**。变压器的铁损取决于电源频率、铁芯中的最大磁通密度、铁芯体积和叠片厚度等。在实际变压器中,铁损的幅值实际上是恒定的且很小。
漏磁通
流过原边绕组的电流产生磁通。连接原边和副边绕组的磁通 $\mathit{\phi _{\mathit{m}}}$ 是有用磁通,称为 **互磁通**。但是,原边电流产生的部分磁通 ($\mathit{\phi _{\mathrm{1}}}$) 不与副边绕组相连。
当负载连接到副边绕组时,电流流过它并产生磁通 ($\mathit{\phi _{\mathrm{2}}}$),该磁通仅与副边绕组相连。因此,仅与其各自绕组相连的 $\mathit{\phi _{\mathrm{1}}}$ 的一部分和磁通 $\mathit{\phi _{\mathrm{2}}}$ 称为 **漏磁通**。
漏磁通的路径通过空气,空气具有非常高的磁阻。因此,原边漏磁通 ($\mathit{\phi _{\mathrm{1}}}$) 的作用是在原边绕组中引入一个与之串联的电抗 ($ \mathit{X_{\mathrm{1}}}$)。类似地,副边漏磁通 ($\mathit{\phi _{\mathrm{2}}}$) 在副边绕组中引入一个与之串联的电抗 ($ \mathit{X_{\mathrm{2}}}$),如图 3 所示。
然而,实际变压器中的漏磁通非常小(约为 $\mathit{\phi _{m}}$ 的 5%),但不能忽略。因为漏磁通的路径是空气,空气具有非常高的磁阻。因此,它需要相当大的磁动势。
铁芯材料的有限磁导率
一般来说,实际变压器的铁芯由高级硅钢制成,它具有特定的相对磁导率 ($\mathit{\mu _{r}}$)。因此,铁芯在一定的磁通密度值下会饱和。因此,实际变压器的铁芯具有有限的磁导率,因此在磁通路径中具有磁阻。
直流变压器
在绪论中,我们将电力变压器定义为交流电机,因为它仅在交流电下工作。因此,变压器不能改变(增加或减少)直流电压的值。在本章中,我们将了解为什么变压器不适用于直流电的原因。
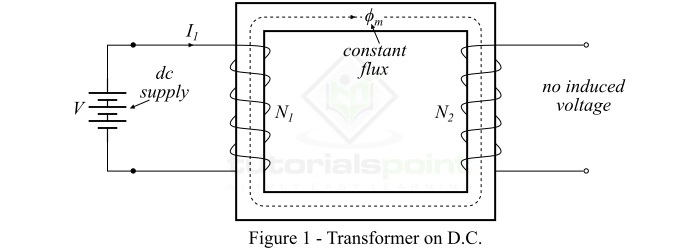
考虑一个如图 1 所示的电力变压器,它连接到电池(或直流电压源)V。当我们将此直流电压 V 加到变压器的原边绕组时,它将吸收恒定电流(直流电),因此会产生恒定的磁通量流过磁芯。
根据电磁感应原理,只有当线圈或导体经受变化的磁场时,才能在线圈或导体中感应电动势,即:
$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
因此,加到原边绕组上的直流电压不会在原边绕组或副边绕组中感应电动势。因此,此讨论证明了 *变压器不适用于直流电源。事实上,将直流电源连接到变压器的原边绕组可能是危险的*。
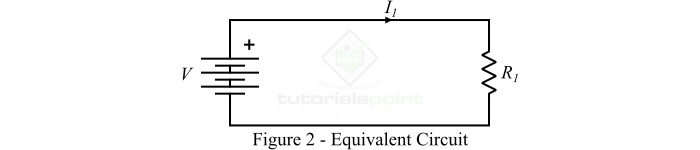
连接到直流电压的变压器的等效原边绕组电路如图 2 所示。在这种情况下,原边绕组中没有自感电动势来阻止外加电压 *V(根据楞次定律)*,原边绕组中的电流由下式给出:
$$\mathrm{\mathit{I_{\mathrm{1}}}\:=\:\frac{\mathit{V}}{\mathit{R_{\mathrm{1}}}}}$$
其中,$\mathit{R_{\mathrm{1}}}$ 是原边绕组的电阻。由于 $\mathit{R_{1}}$ 的值很小,因此流过原边绕组的电流 $\mathit{I_{\mathrm{1}}}$ 将非常大。这种大电流会导致变压器过热和烧毁,或者保险丝会熔断。因此,*我们绝不能将变压器的原边绕组连接到直流电源,因为它可能会损坏变压器或造成触电事故*。
变压器的损耗
实际变压器中可能发生以下功率损耗:
铁损或铁芯损耗
铜损或 $\mathit{I^{2}R}$ 损耗
杂散损耗
介质损耗
在变压器中,这些功率损耗以热量的形式出现,并导致两个主要问题:
增加变压器的温度。
降低变压器的效率。
铁损或铁芯损耗
**铁损** 是由于交变磁通流过变压器的磁芯而产生的。由于这个原因,铁损也称为 **铁芯损耗**。我们通常用符号 ($\mathit{P_{i}}$) 表示铁损。铁损包括磁滞损耗 ($\mathit{P_{h}}$) 和涡流损耗 ($\mathit{P_{e}}$)。因此,铁损由磁滞损耗和涡流损耗之和给出,即
$$\mathrm{\mathrm{铁损,}\mathit{P_{i}}\:=\:\mathrm{磁滞损耗(\mathit{P_{h}})}\:+\:\mathrm{涡流损耗(\mathit{P_{e}})}}$$
通过对变压器进行 **开路试验** 来确定磁滞损耗和涡流损耗(或铁损)。
磁滞损耗和涡流损耗的经验公式为:
$$\mathrm{\mathit{P_{h}}\:=\:\mathit{k_{h}f\:B_{m}^{x}}\:\cdot \cdot \cdot (1)}$$
$$\mathrm{\mathit{P_{e}}\:=\:\mathit{ke\:B_{m}^{\mathrm{2}}\:f^{\mathrm{2}}t^{\mathrm{2}}}\:\cdot \cdot \cdot (2)}$$
其中:
$\mathit{B_{m}}$ 的指数,即“$\mathit{x}$”称为 **Steinmetz 常数**。根据铁芯材料的特性,其值在 1.5 到 2.5 之间。
**$\mathit{k_{h}}$** 是一个比例常数,其值取决于铁芯材料的体积和质量。
**$\mathit{k_{e}}$** 是一个比例常数,取决于铁芯材料的体积和电阻率。
**$\mathit{f}$** 是铁芯中交变磁通的频率。
**$\mathit{B_{m}}$** 是铁芯中的最大磁通密度。
**$\mathit{t}$** 是每个铁芯叠片的厚度。
因此,总铁损或铁芯损耗也可以写成:
$$\mathrm{\mathit{P_{i}}\:=\:\mathit{k_{h}f\:B_{m}^{x}}\:+\:\mathit{ke\:B_{m}^{\mathrm{2}}\:f^{\mathrm{2}}t^{\mathrm{2}}}\:\cdot \cdot \cdot (3)}$$
由于变压器的输入电压近似等于原边绕组中的感应电压,即
$$\mathrm{\mathit{V_{\mathrm{1}}}\:=\:\mathit{E_{\mathrm{1}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{1}}}}$$
$$\mathrm{\Rightarrow \mathit{V_{\mathrm{1}}}\:=\:4.44\:\mathit{f\:B_{m}AN_{\mathrm{1}}}}$$
其中,$\mathit{A}$ 是变压器铁芯的横截面积,$\mathit{N_{1}}$ 是原边绕组的匝数,$\mathit{f}$ 是电源频率。
$$\mathrm{\therefore \mathit{B_{m}}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{4.44\mathit{fAN_{\mathrm{1}}}}\:\cdot \cdot \cdot (4)}$$
因此,根据公式 (1) 和 (4),我们得到:
$$\mathrm{\mathit{P_{h}}\:=\:\mathit{k_{h}f}\left ( \frac{\mathit{V_{\mathrm{1}}}}{4.44\mathit{fAN_{\mathrm{1}}}} \right )^{x}}$$
$$\mathrm{\Rightarrow \mathit{P_{h}}\:=\:\mathit{k_{h}f}\left ( \frac{\mathrm{1}}{4.44\mathit{AN_{\mathrm{1}}}} \right )^{x}\cdot \left ( \frac{\mathit{V_{\mathrm{1}}}}{\mathit{f}} \right )^{x}}$$
$$ \mathrm{\Rightarrow \mathit{P_{h}}\:=\:\mathit{k_{h}}\left ( \frac{\mathrm{1}}{4.44\mathit{AN_{\mathrm{1}}}} \right )^{x}\cdot \mathit{V_{\mathrm{1}}^{x}}\:\mathit{f^{(\mathrm{1}-x)}}\:\cdot \cdot \cdot (5)} $$
因此,公式 (5) 表明 *磁滞损耗取决于输入电压和电源频率*。
同样,由公式 (2) 和 (4),我们得到:
$$ \mathrm{\mathit{P_{e}}\:=\:\mathit{k_{e}f^{\mathrm{2}}t^{\mathrm{2}}}\left ( \frac{\mathit{V_{\mathrm{1}}}}{4.44\mathit{fAN_{\mathrm{1}}}} \right )^{\mathrm{2}}} $$
$$ \mathrm{\Rightarrow \mathit{P_{e}}\:=\:\mathit{k_{e}\left ( \frac{\mathit{V_{\mathrm{1}}}}{\mathrm{4.44}\mathit{AN_{\mathrm{1}}}} \right )^{\mathrm{2}}\mathit{t^{\mathrm{2}}}\:\cdot \cdot \cdot \mathrm{(6)}}} $$
因此,从公式 (6) 可以得出结论:*变压器中的涡流损耗与输入电压的平方成正比,并且与电源频率无关*。
因此,总铁损也可以写成:
$$ \mathrm{\mathit{P_{i}}\:=\:\mathit{k_{h}\left ( \frac{\mathrm{1}}{\mathrm{4.44}\mathit{AN_{\mathrm{1}}}} \right )^{\mathrm{2}}\cdot \mathit{V_{\mathrm{1}}^{\mathit{x}}f^{(\mathrm{1-x})}}\:+\:\mathit{k_{e}}\left ( \frac{V_{\mathrm{1}}}{\mathrm{4.44}\mathit{AN_{\mathrm{1}}}} \right )^{\mathrm{2}}\mathit{t^{\mathrm{2}}}\:\cdot \cdot \cdot \left ( \mathrm{7} \right )}} $$
在实际应用中,变压器连接到恒定频率和恒定电压的电源,因此,*f* 和 *Bm* 均为常数。因此,铁损在所有负载下实际上保持不变。
我们可以通过使用高硅含量钢材来构成变压器铁芯来减少磁滞损耗,同时可以通过使用薄层叠铁芯代替实心铁芯来最大限度地减少涡流损耗。对变压器进行 **空载试验** 以确定铁损。
铜损或 $\mathit{I^{2}R}$ 损耗
变压器中由于初级和次级绕组的欧姆电阻而产生的功率损耗称为 **铜损或 I²R 损耗**。我们通常用 Pc 表示铜损。因此,变压器的总铜损是初级绕组功率损耗和次级绕组功率损耗之和,即:
$$ \mathrm{\mathit{P_{c}}\:=\:\mathrm{初级绕组铜损\:+\:次级绕组铜损}} $$
$$ \mathrm{\Rightarrow \mathit{P_{c}}\:=\:\mathit{I_{\mathrm{1}}^{\mathrm{2}}}\mathit{R_{\mathrm{1}}}\:+\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}}\mathit{R_{\mathrm{2}}}\:\cdot \cdot \cdot (8)} $$
因为:
$$\mathrm{\mathit{I_{\mathrm{1}}}\mathit{N_{\mathrm{1}}}\:=\:\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}}$$
$$ \mathrm{\Rightarrow \mathit{I_{\mathrm{1}}}\:=\:\left ( \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}} \right )\mathit{I_{\mathrm{2}}}\:\cdot \cdot \cdot (9)} $$
$$ \mathrm{\therefore \mathit{P_{c}}\:=\:\left [ \left ( \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}} \right )I_{\mathrm{2}} \right ]^{\mathrm{2}}\:\mathit{R_{\mathrm{1}}}\:+\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}}\mathit{R_{\mathrm{2}}}\:=\:\left [ \left ( \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}} \right )^{\mathrm{2}}\mathit{R_{\mathrm{1}}}\:+\:\mathit{R_{\mathrm{2}}} \right ]\mathit{I_{\mathrm{2}}^{\mathrm{2}}}\:\cdot \cdot \cdot (10)} $$
从公式 (10) 可以清楚地看出,*变压器的铜损随负载电流的平方而变化*。因此,铜损也称为“可变损耗”,因为在实际应用中,变压器承受可变负载,因此具有可变负载电流。
我们对变压器进行“短路试验”以确定其铜损的值。在实际变压器中,铜损约占变压器总功率损耗的 90%。
杂散损耗
在实际变压器中,一部分总磁通沿空气路径传播,这部分磁通称为 **漏磁通**。该漏磁通会在导电或金属部件(如变压器油箱)中产生涡流。这些涡流会导致功率损耗,这被称为 **杂散损耗**。
介质损耗
变压器绝缘材料(如油、固体绝缘等)中发生的功率损耗称为 **介质损耗**。介质损耗仅在高压变压器中才显著。
虽然在实际应用中,杂散损耗和介质损耗非常小,且为常数,可以忽略不计。
从以上讨论可以看出,变压器存在一些恒定损耗和一些可变损耗。因此,我们可以将变压器中的损耗分为两种类型,即 **恒定损耗** 和 **可变损耗**。
因此,变压器的总损耗是恒定损耗和可变损耗之和,即:
Total losses in transformer = Constant losses + Variable losses
变压器的效率
变压器效率
变压器的输出功率与输入功率之比称为 **变压器效率**。变压器效率用希腊字母 Eta (η) 表示。
$$ \mathrm{效率, \eta \:=\:\frac{输出功率}{输入功率}} $$
根据此定义,似乎我们可以通过直接加载变压器并测量输入功率和输出功率来确定变压器的效率。但是,这种效率测定方法存在以下缺点:
在实际应用中,变压器的效率非常高,输入和输出瓦特表中很小的误差(例如 1%)可能会导致荒谬的结果。因此,这种方法可能会得出效率超过 100% 的结果。
在这种方法中,变压器已加载,因此会浪费相当多的功率。因此,对于大型变压器,这种方法在经济上不可行。
很难找到能够吸收所有输出功率的负载。
这种方法不会提供有关变压器损耗的任何信息。
因此,由于这些限制,很少使用直接加载法来确定变压器的效率。在实际应用中,我们使用空载试验和短路试验来确定变压器效率。
对于实际变压器,输入功率由下式给出:
$$ \mathrm{输入功率\:=\:\mathrm{输出功率\:+\:损耗}} $$
因此,变压器效率也可以使用以下表达式计算:
$$ \mathrm{\eta \:=\:\frac{输出功率}{输出功率\:+\:损耗}} $$
$$ \mathrm{\Rightarrow \eta \:=\:\frac{VA\times 功率因数}{\left ( VA\times 功率因数 \right )\:+\:损耗}} $$
其中:
$$ \mathrm{输出功率\:=\:VA\times 功率因数} $$
并且,损耗可以通过变压器测试来确定。
根据变压器试验得到的效率
当我们进行变压器测试时,会得到以下结果:
根据空载试验:
$$ \mathrm{额定负载铁损\:=\:\mathit{P_{i}}} $$
根据短路试验:
$$ \mathrm{额定负载铜损\:=\:\mathit{P_{c}}} $$
因此,变压器满载时的总损耗为
$$ \mathrm{总满载损耗\:=\:\mathit{P_{i}+\:P_{c}}} $$
现在,我们能够在任何功率因数下确定变压器的满载效率,而无需实际加载变压器。
$$ \mathrm{\mathit{n_{FL}}\:=\:\frac{(VA)_{\mathit{FL}}\times 功率因数}{[(VA)_{\mathit{FL}}\times 功率因数]+\:\mathit{P_{i}}+\mathit{P_{c}}}} $$
此外,变压器在任何等于 *x × 满载* 的负载下的效率。其中,x 是负载的比例。在这种情况下,对应于给定负载的总损耗为:
$$ \mathrm{(总损耗)_{x}\:=\:\mathit{P_{i}+\:x^{\mathrm{2}}\mathit{P_{c}}}} $$
这是因为铁损 (Pi) 是恒定损耗,因此在所有负载下都保持不变,而铜损与负载电流的平方成正比。
$$ \mathrm{\therefore\eta _{x}\:=\: \frac{\mathit{x}\times (VA)_{\mathit{FL}}\times 功率因数}{[\mathit{x}\times (VA)_{\mathit{FL}}\times 功率因数]+\:\mathit{P_{i}}+\:x^{\mathrm{2}}\mathit{P_{c}}}} $$
最大效率的条件
对于给定的变压器,我们有:
$$ \mathrm{输出功率\:=\:\mathit{V_{\mathrm{2}}I_{\mathrm{2}}cos\phi _{\mathrm{2}}}} $$
设变压器参考次级侧,则 *Ro2* 是变压器的总电阻。总铜损由下式给出:
$$ \mathrm{\mathit{P_{c}}\:=\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}\mathit{R_{o\mathrm{2}}}}} $$
因此,变压器效率由下式给出:
$$ \mathrm{\eta \:=\:\frac{\mathit{V_{\mathrm{2}}}I_{\mathrm{2}}cos\phi _{\mathrm{2}}}{\mathit{V_{\mathrm{2}}I_{\mathrm{2}}cos\phi _{\mathrm{2}}}+\mathit{P_{i}}+\mathit{I_{\mathrm{2}}^{\mathrm{2}}}R_{o\mathrm{2}}}} $$
重新排列表达式,我们得到:
$$ \mathrm{\eta \:=\:\frac{\mathit{V_{\mathrm{2}}}cos\phi _{\mathrm{2}}}{\mathit{V_{\mathrm{2}}cos\phi _{\mathrm{2}}}+\left ( \mathit{\frac{P_{i}}{I_{\mathrm{2}}}} \right )+\mathit{I_{\mathrm{2}}}R_{o\mathrm{2}}}\:=\:\mathit{\frac{V_{\mathrm{2}}cos\phi _{\mathrm{2}}}{D}}\:\cdot \cdot \cdot (1)} $$
在实际应用中,次级电压 *V2* 近似恒定。因此,对于给定功率因数的负载,变压器效率取决于负载电流 (*I2*)。从公式 (1) 可以看出,分子是常数,为了使效率最大化,分母 (D) 应最小,即
$$ \mathrm{\mathit{\frac{d(D)}{dI_{\mathrm{2}}}}\:=\:0} $$
$$ \mathrm{\Rightarrow\mathit{\frac{d}{dI_{\mathrm{2}}}}\left [ \mathit{V_{\mathrm{2}}cos\phi _{\mathrm{2}}}+\left ( \mathit{\frac{P_{i}}{I_{\mathrm{2}}}}\right )+\mathit{I_{\mathrm{2}} R_{0\mathrm{2}}} \right ]\:=\:0} $$
$$ \mathrm{\Rightarrow 0-\left ( \mathit{\frac{P_{i}}{I_{\mathrm{2}}}} \right )+\mathit{R_{o\mathrm{2}}}\:=\:0} $$
$$ \mathrm{\Rightarrow \mathit{P_{i}}\:=\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}R_{o\mathrm{2}}}} $$
$$ \mathrm{\Rightarrow 铁损\:=\:铜损} $$
因此,*对于给定的功率因数,当恒定铁损等于可变铜损时,变压器的效率最大*。
任何负载下的最大效率由下式给出:
$$ \mathrm{\mathit{\eta _{max}}\:=\:\frac{\mathit{x\times (VA)_{\mathit{FL}}\times 功率因数}}{[\mathit{x\times (VA)_{\mathit{FL}}}\times 功率因数]+\:2\mathit{P_{i}}}} $$
此外,对应于变压器最大效率的负载电流 (*I2*) 为:
$$ \mathrm{\mathit{I_{\mathrm{2}}}\:=\:\sqrt{\frac{\mathit{P_{i}}}{R_{o2}}}} $$
数值例子
在一个 100 kVA 的变压器中,铁损为 450 W,满载铜损为 900 W。求该变压器在满载时的效率和最大效率,其中负载功率因数为 0.8 滞后。
解答
已知数据:
满载 VA = 100 kVA = 100 × 1000 VA
铁损,Pi = 450 W
铜损,Pc = 900 W
cosφ2 = 0.8
变压器满载效率:
$$ \mathrm{总损耗\:=\:450\:+\:900\:=\:1350\:W} $$
$$ \mathrm{\mathit{\eta _{\mathit{FL}}}\:=\:\frac{(VA)_{\mathit{FL}}\times 功率因数}{[(VA)_{\mathit{FL}}\times 功率因数]+\:总损耗}} $$
$$ \mathrm{\Rightarrow \mathit{\eta _{\mathit{FL}}}\:=\:\frac{100\times 1000\times 0.8}{(100\times 1000\times 0.8)+1350}\:=\:\frac{80000}{81350}\:=\:0.9834} $$
$$ \mathrm{\therefore \eta _{\mathit{FL}}\:=\:0.9834\times 100\%\:=\:98.34\%} $$
变压器的最大效率:
对于最大效率:
$$ \mathrm{铁损\:=\:铜损} $$
$$ \mathrm{\therefore \eta _{\mathit{max}}\:=\:\frac{(VA)_{\mathit{FL}}\times 功率因数}{[(VA)_{\mathit{FL}}\times 功率因数]+2\mathit{P_{i}}}} $$
$$ \mathrm{\Rightarrow \eta _{\mathit{max}}\:=\:\frac{100\times 1000\times 0.8}{(100\times 1000\times 0.8)+(2\times 450)}\:=\:0.9888} $$
$$ \mathrm{\therefore \eta _{\mathit{max}}\:=\:0.9888\times 100\%\:=\:98.88\%} $$
三相变压器
在实际应用中,电力是通过三相系统发电、传输和分配的。因此,我们需要 **三相变压器** 来在电力系统网络的各个阶段升压或降压。
我们可以通过以下两种方式之一来构造三相变压器:
我们可以连接三个独立的单相变压器来进行三相运行。这种布置被称为 **三相变压器组**。
我们可以构造一个单一的具有磁芯和所有三个相绕组的三相变压器。整个组件组合在一个单一结构中。
三相变压器的绕组可以按以下方式连接:
**星形-星形连接** - 在这种情况下,初级和次级绕组都采用星形连接。
**三角形-三角形连接** - 在这种情况下,初级和次级绕组都采用三角形连接。
Δ-Y 接法 − 此接法中,原边绕组采用三角形连接,副边绕组采用星形连接。
Y-Δ 接法 − 此接法中,原边绕组采用星形连接,副边绕组采用三角形连接。
三相变压器的结构
三相变压器可以通过两种方式构造,即核心式结构和壳式结构。
核心式结构
在三相变压器的核心式结构中,磁芯具有三个垂直铁心柱和两个水平横截面,如图 1 所示。此处,每一铁心柱上都放置一对原边和副边绕组。低压 (lv) 绕组放置在磁芯旁边,高压 (hv) 绕组绕在 lv 绕组周围。
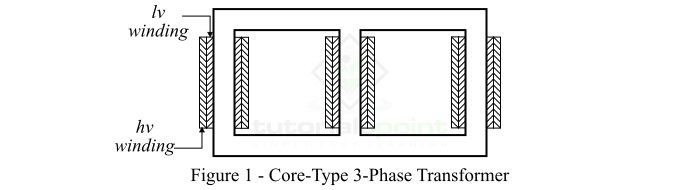
壳式结构
壳式三相变压器可以通过将三个单相壳式变压器堆叠在一起构成,如图 2 所示。在这种情况下,原边和副边绕组都放置在中心铁心柱上,两个外侧铁心柱作为磁通路径。壳式三相变压器的行为与三台单相变压器组几乎相同。
三台单相变压器组的优点
与三相单元变压器相比,三台单相变压器组的主要优点如下:
当变压器组中的一台单相变压器损坏并与系统隔离时,剩余的两台变压器可在开三角形连接中供电。
在变压器组中,可以提供 kVA 额定值高于其他变压器的单相变压器以供应不平衡负载。
对于三台单相变压器组,备用要求较低。
运输单相变压器比运输三相变压器更方便。
三相单元变压器的优点
对于相同的 kVA 额定值,三相单元变压器与三台单相变压器组相比具有以下优点:
三相单元变压器体积更小,重量更轻,成本更低。
它比变压器组效率更高。
安装简单。
根据需要,我们同时使用变压器组和三相单元变压器。但是,通常的做法是使用三相单元变压器。
变压器的类型
根据原边和副边绕组的匝数,变压器可以分为以下三种类型:
升压变压器
降压变压器
一比一变压器
根据应用,我们可以将变压器分为以下三种主要类型:
电力变压器
配电变压器
仪用变压器
升压变压器
副边绕组匝数大于原边绕组匝数的变压器,其输出电压大于输入电压,称为升压变压器。在电力系统中,升压变压器用于将低电压升高到更高的值以进行传输。
降压变压器
副边绕组匝数小于原边绕组匝数的变压器,其输出电压小于输入电压,称为降压变压器。在电力系统中,降压变压器用于将高电压降低到较低的电压值,用于配电和利用。
一比一 (1:1) 变压器
原边绕组和副边绕组匝数相同的变压器,其输出电压等于输入电压,称为一比一变压器。也称为隔离变压器。它应用于需要将两个电路电隔离但磁耦合以进行能量传输的领域。
电力变压器
伏安 (VA) 额定值较高的变压器,通常为兆伏安或吉伏安级,称为电力变压器。电力变压器设计为以几乎恒定的负载运行,该负载等于其额定值。这些变压器用于发电站、接收站和电力传输线路末端的变电站,用于升压或降压。
实际上,电力变压器在负荷期间投入运行,而在轻负荷期间断开连接。这些变压器设计为在满载或接近满载时具有最大效率。但是,电力变压器的设计具有相当高的漏抗。因此,对于电力变压器,高漏抗的限流作用比电压调整更重要。
配电变压器
用于将高电压降低到低电压以进行配电的变压器称为配电变压器。配电变压器设计为以可变负载运行,该负载远小于其额定值。因此,这些变压器设计为在负载为满载的 ½ 到 ¾ 之间时具有最大效率。配电变压器全天候运行,无论是否承载任何负载。
仪用变压器
很难用简单的测量设备测量高交流电流和电压。因此,为了简化高交流电流和电压的测量,我们使用专门设计的变压器,称为仪用变压器。通过使用仪用变压器,我们可以用低量程交流测量设备测量高交流量。
根据变换量的类型,仪用变压器分为以下两种类型:
电流互感器 (C.T.)
电压互感器 (P.T.)
电流互感器
电流互感器是一种仪用变压器,用于将电力线路的高交流电流降低到可测量的低值。基本上,电流互感器是一种升压降流变压器。它有一个几匝粗导线的原边绕组和一个多匝细导线的副边绕组。电流互感器的原边绕组与需要测量电流的线路串联连接,副边绕组与低量程交流电流表连接以测量和指示电流。
电压互感器
电压互感器是一种降压变压器,用于将高线路电压降低到可测量的值。电压互感器的原边绕组匝数很多,而副边绕组匝数很少。原边绕组连接到需要测量电压的电力线路,副边绕组连接到低量程交流电压表以指示测得的电压值。
直流电机的构造
能够将直流电 (dc) 能量转换为机械能或将机械能转换为直流电 (dc) 能量的机电设备称为直流电机。
如果直流电机将直流电能转换为机械能,则称为直流电动机。如果电机将机械能转换为直流电能,则称为直流发电机。直流电动机和直流发电机的结构相似。
典型的直流电机包含以下主要部件:
机座或机架
电枢
励磁系统
换向器
电刷
轴承
直流电机的示意图如下所示:
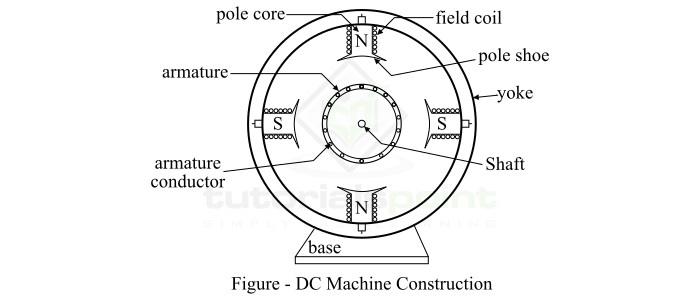
现在让我们更详细地讨论每个组件。
机座或机架
机座是直流电机的外部框架。它由具有高磁导率和高机械强度的材料制成。实际上,直流电机的机座由铸钢制成。
直流电机的机座或机架具有以下主要用途:
它保护内部机器部件(如电枢、绕组、磁极等)免受机械损坏。
机座容纳磁场系统。
它为工作磁通提供低磁阻路径。
它通过轴承支撑转子或电枢。
电枢
在直流电机(电动机或发电机)中,电枢是可以在支撑轴承上自由旋转的导体或线圈系统。工作转矩和电动势在电枢线圈中产生。电枢由两个主要部分组成,即电枢铁芯和电枢绕组。
电枢铁芯是一个实心圆柱形结构,由高磁导率的薄硅钢片制成。在铁芯的外圆周上切割槽以承载电枢绕组。
电枢绕组由铜线制成。直流电机的电枢绕组通常是模制绕组。根据电枢导体的端部连接方式,电枢绕组可以分为两种类型,即叠绕组和波绕组。绕组类型决定了电机的电压和电流额定值。对于叠绕组,电流流动的并联支路数 (A) 等于电机中的磁极数 (P)。另一方面,对于波绕组,并联支路数 (A) 等于 2。
励磁系统
励磁系统是直流电机的一部分,它在电机中产生工作磁通。它基本上是一个由直流电源励磁的电磁体系统。在直流电机中,励磁系统是电机的静止部分,它固定在电机的机座或机架上。直流电机励磁系统主要有三部分:磁极铁芯、磁极靴和励磁绕组。
磁极铁芯由薄钢片制成。磁极铁芯的一端固定在机架上,另一端有磁极靴。磁极铁芯承载励磁绕组。
磁极靴是磁极铁芯的突出部分,具有较大的横截面积。磁极靴有助于在气隙中均匀地分布磁通,并为磁通提供低磁阻路径。它也支撑励磁绕组。
励磁绕组由铜线制成。励磁绕组是模制绕组,并绕在磁极铁芯周围。当励磁绕组由直流电源励磁时,它们会变成电磁体并在电机中产生磁通。
换向器
换向器是直流电机的重要部件之一。它基本上是机械整流器。它是一个圆柱形装置,由铜制成。换向器的外圆周有 V 形槽,用于承载换向片。换向片是插入槽中的铜条。这些片段由云母彼此绝缘。换向器安装在直流电机轴上,位于电枢的一侧。电枢导体借助铜耳连接到换向片。
换向器执行以下两个主要功能:
在直流发电机中,它从电枢导体收集电流。在直流电动机中,它向电枢导体供电。
借助电刷,它将电枢的交流电转换为外部电路中的单向电流,反之亦然。
电刷
电刷用于与旋转的换向器进行电气连接。它们从(或向)运动的换向器收集(或供应)电流。电刷通常由碳制成。它们装在电刷架中,并借助弹簧压力与换向器表面接触。
轴承
直流电机中使用轴承来减少摩擦损失。因此,直流电机中轴承的主要功能是以最小的摩擦支撑电机轴。在直流电机中,通常使用滚珠轴承或滚柱轴承。
直流电机的类型
直流电机是一种将直流形式的电能转换为机械能,或将机械能转换为直流形式的电能的装置。因此,直流电机基本上是一种机电能量转换装置。
根据能量转换,直流电机可分为以下两种类型:
直流电动机
直流发电机
直流电动机和直流发电机的基本结构几乎相同。然而,直流电动机和直流发电机运行中涉及的基本原理是不同的。
每个直流电机都包含一套导体系统和一套磁体或电磁体系统。导体系统称为电枢,在直流电机中,它安装在可移动的轴上。磁体或电磁体系统称为励磁系统,它产生所需的工磁通量。
直流电动机
图1显示了直流电动机的框图。(此处应插入图1)
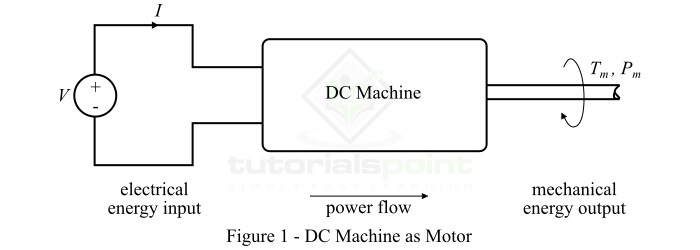
当直流电机设计用于将直流电能转换为旋转机械能时,它被称为直流电动机。因此,在直流电动机的情况下,电能通过输入端子供给电机,机械能输出则以轴的旋转形式从轴上获取。
直流发电机
图2显示了直流发电机的框图。(此处应插入图2)
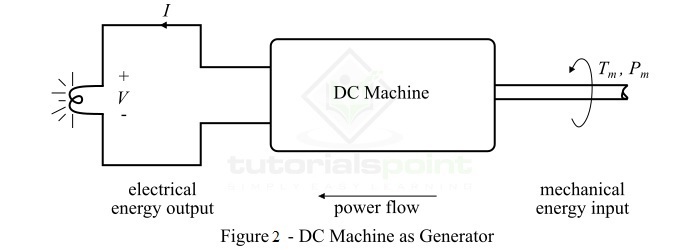
能够将机械能输入转换为电能输出的直流电机称为直流发电机。因此,在直流发电机中,来自发动机、涡轮机等能源的机械能以轴的旋转能的形式提供给直流电机,直流电能则作为输出从电枢端子获得。
直流发电机的原理
直流发电机的运行原理基于法拉第电磁感应定律。根据该定律,当穿过导体或线圈的磁通量发生变化时,导体或线圈中就会感应出电动势。该感应电动势的大小由下式给出:
$${\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\:\cdot \cdot \cdot (1)}}$$
其中,$\phi$是线圈的磁通链,N是线圈的匝数。
在直流发电机的情况下,磁通量 ($\phi$) 保持静止,线圈旋转。线圈旋转而磁通静止时感应的电动势称为动态感应电动势。
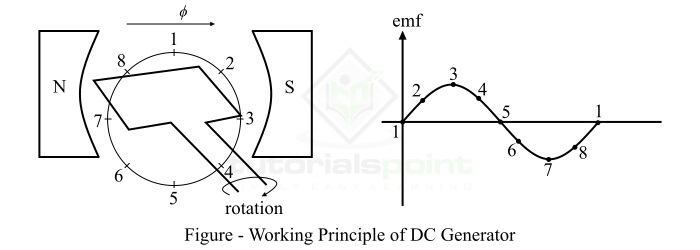
为了理解直流发电机的运行原理,我们考虑一个单环直流发电机(即 *N = 1*),如图所示。(此处应插入图示) 此处,线圈由某个原动机(机械能的来源)旋转,并且线圈的磁通链发生变化。
设 $\phi$ 为电机每个磁极产生的平均磁通量,则发电机中的平均感应电动势由下式给出:
$${\mathrm{\mathit{E_{av}}\:=\:\frac{\mathit{d\phi }}{\mathit{dt}}\:=\:\mathrm{线圈每秒切割的磁通量}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{一次旋转切割的磁通量\:\times \:每秒旋转次数}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{\left ( 每极磁通量\times 极数 \right )}\:\times \:\mathrm{每秒旋转次数}}}$$
$${\mathrm{\therefore \mathit{E_{av}}\:=\:\mathit{\phi \:\times P\:\times \:n}\:\cdot \cdot \cdot (2)}}$$
其中,*P* 是发电机的总极数,*n* 是线圈的每秒旋转速度。公式(2)给出了单环直流发电机中的平均感应电动势。
以下几点解释了直流发电机的运行原理:
位置1 - 感应电动势为零,因为线圈边的运动与磁通量平行。
位置2 - 线圈边与磁通量成一定角度运动,因此在环路中产生较小的电动势。
位置3 - 线圈边与磁通量成直角运动,因此感应电动势最大。
位置4 - 线圈边以一定角度切割磁通量,因此在线圈边中感应出较小的电动势。
位置5 - 线圈边没有与磁通量发生链结,并且线圈边与磁通量平行移动。因此,在线圈中没有感应电动势。
位置6 - 线圈边在相反极性磁极下移动,因此感应电动势的极性反转。最大电动势将在此方向上在位置7感应,而在位置1时为零。这个循环随着线圈的旋转而重复。
这样,就在直流发电机中感应出电动势。尽管这种感应电动势本质上是交流电,但随后可以使用称为换向器的装置将其转换为单向电动势。
直流发电机电枢导体中感应电动势的方向由弗莱明右手定则 (FRHR) 决定,我们在本教程的 *模块 1(基本概念)* 中讨论过。
直流发电机的电动势方程
给出直流发电机中产生的电动势大小的表达式称为直流发电机的电动势方程。我们现在将推导出直流发电机中感应电动势的表达式。
设:
$\phi$ = 每极磁通
*P* = 发电机的极数
*Z* = 电枢导体数
*A* = 并联支路数
*N* = 电枢转速 (RPM)
*E* = 产生的电动势
因此,电枢一次旋转时一个导体切割的磁通量(以韦伯为单位)由下式给出:
$${\mathrm{\mathit{d\phi \:=\:P\times \phi }}}$$
如果 N 是每分钟的转数,则完成一次旋转所需的时间(以秒为单位)为:
$${\mathrm{\mathit{dt \:=\frac{60}{N}}}}$$
根据法拉第电磁感应定律,每个导体感应的电动势由下式给出:
$${\mathrm{\mathrm{每导体电动势}\:=\:\mathit{\frac{d\phi }{dt}}\:=\:\frac{\mathit{P\phi }}{\mathrm{\left ( {60/\mathit{N}} \right )}}\:=\:\frac{\mathit{P\phi N}}{\mathrm{60}}}}$$
发电机产生的总电动势等于每个并联支路的电动势,它是每导体电动势与每个并联支路串联导体数的乘积,即:
$${\mathrm{\mathit{E}\:=\:\left ( 每导体电动势 \right )\times \left ( 每并联支路导体数 \right )}}$$
$${\mathrm{\Rightarrow \mathit{E}\:=\:\frac{\mathit{P\phi N}}{60}\times \frac{\mathit{Z}}{\mathit{A}}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:\frac{\mathit{NP\phi Z}}{60\mathit{A}}\:\cdot \cdot \cdot \left ( 1 \right )}}$$
公式 (1) 称为 *直流发电机的电动势方程*。
对于波绕组:
$${\mathrm{\mathrm{并联支路数,}\mathit{A}\:=\:2}}$$
$${\mathrm{\therefore \mathit{E}\:=\:\frac{\mathit{NP\phi Z}}{\mathrm{120}}}}$$
对于叠绕组:
$${\mathrm{\mathrm{并联支路数,}\mathit{A}\:=\:\mathit{P}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:\frac{\mathit{N\phi Z}}{\mathrm{60}}}}$$
对于给定的直流发电机,*Z、P* 和 *A* 是常数,因此产生的电动势 (E) 与每极磁通 ($\phi$) 和电枢旋转速度 (*N*) 成正比。
数值例子
一台 6 极直流发电机具有 600 个电枢导体和 0.06 Wb 的有用磁通量。如果它是波绕组连接和叠绕组连接,并且以 1000 RPM 的速度运行,则产生的电动势是多少?
解答
已知数据:
极数,*P* = 6
电枢导体数,*Z* = 600
每极磁通量,$\phi$ = 0.06 Wb
电枢转速,*N* = 1000 RPM
对于波绕组连接的发电机:
$${\mathrm{\mathit{E}\:=\:\frac{\mathit{NP\phi Z}}{\mathrm{120}}}}$$
$${\mathrm{\Rightarrow \mathit{E}\:=\:\frac{1000\times6\times 0.06\times 600}{120}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:1800\:V}}$$
对于叠绕组连接的发电机:
$${\mathrm{\mathit{E}\:=\:\frac{\mathit{N\phi Z}}{\mathrm{60}}}}$$
$${\mathrm{\Rightarrow \mathit{E}\:=\:\frac{1000\times 0.06\times 600}{60}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:600\:V}}$$
直流发电机的类型
在实际的直流发电机中,磁场是由电磁体而不是永磁体产生的。然后根据励磁绕组在发电机电路中的连接方式对直流发电机进行分类。在此基础上,直流发电机可分为以下两种类型:
他励直流发电机
自励直流发电机
他励直流发电机
磁场绕组由独立的直流电源(如电池)励磁的直流发电机称为他励直流发电机。图1显示了自励直流发电机的连接图。(此处应插入图1)
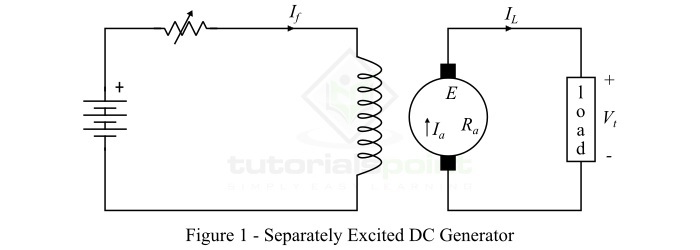
他励直流发电机产生的电压取决于电枢旋转速度和励磁电流(即电机中的磁通量)。电枢速度和励磁电流越大,发电机中感应的电动势越大。然而,他励直流发电机很少用于实际应用中,因为它们需要外部直流电源进行励磁。
自励直流发电机
磁场绕组由发电机本身的输出励磁的直流发电机称为自励直流发电机。根据励磁绕组与电枢的连接方式,自励直流发电机可分为以下三种类型:
串励直流发电机
并励直流发电机
复励直流发电机
串励直流发电机
励磁绕组与电枢串联,使整个电枢电流流过励磁绕组和负载的直流发电机称为串励直流发电机。图2显示了串励直流发电机的连接图。(此处应插入图2)
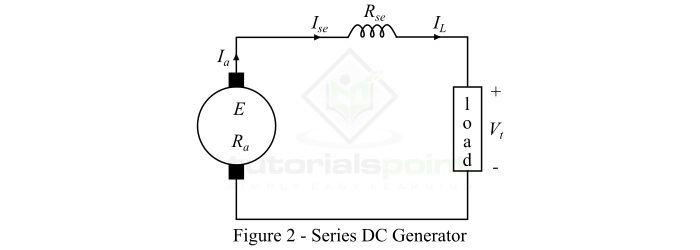
在串励直流发电机的情况下,励磁绕组承载整个负载电流,因此它由粗导线和少量匝数组成,因此其电阻最小。串励直流发电机用于提升机等特殊应用。
以下是一些串励直流发电机的重要表达式:
$${\mathrm{\mathrm{电枢电流,}\mathit{I_{a}}\:=\:\mathit{I_{se}}\:=\:\mathit{I_{L}}}}$$
其中,$\mathit{I_{se}}$ 是串励磁电流,$\mathit{I_{L}}$ 是负载电流。
$${\mathrm{\mathrm{端电压,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}\left ( \mathit{R_{a}+R_{se}} \right )}}}}$$
其中,*E* 是产生的电动势,$\mathit{R_{a}}$ 是电枢电路电阻,$\mathit{R_{se}}$ 是串励磁电阻。
并励直流发电机
励磁绕组与电枢绕组并联,使发电机的端电压加在其上的直流发电机称为并励直流发电机。图3显示了并励直流发电机的连接图。(此处应插入图3)
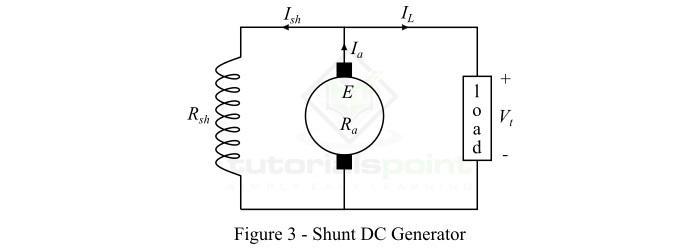
在并励直流发电机中,并励磁绕组具有大量细导线匝数,因此电阻较大,因此只有一部分电枢电流流过它,其余部分流过负载。
以下是一些并励直流发电机的重要表达式:
$${\mathrm{\mathrm{电枢电流,}\mathit{I_{a}}\:=\:\mathit{I_{L}+I_{sh}}}}$$
$${\mathrm{\mathrm{并励磁电流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{t}}}{\mathit{R_{sh}}}}}$$
$${\mathrm{\mathrm{端电压,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}R_{a}}}}$$
复励直流发电机
复励直流发电机是指在每个磁极上都有两组励磁绕组的直流发电机——一个与电枢绕组串联,另一个与电枢绕组并联。复励直流发电机可进一步分为以下两种类型:
短 shunt 复励直流发电机
长 shunt 复励直流发电机
短 shunt 复励直流发电机是指只有并励磁绕组与电枢绕组并联的直流发电机,如图4所示。(此处应插入图4)
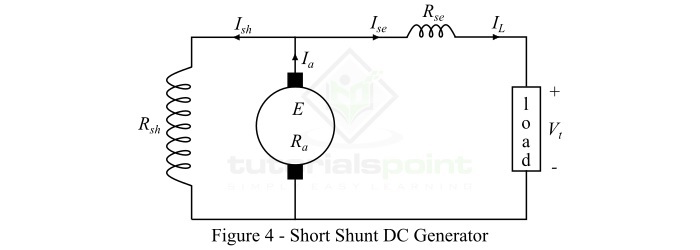
长 shunt 复励直流发电机是指并励磁绕组与串励磁绕组和电枢绕组都并联的直流发电机,如图5所示。(此处应插入图5)
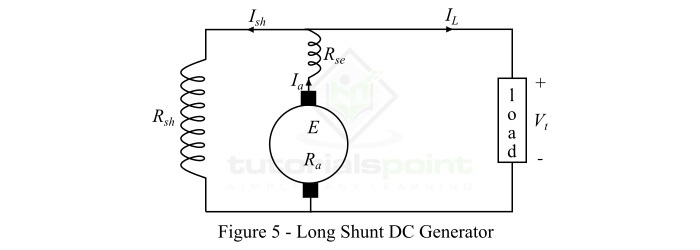
以下是复励直流发电机的重要表达式:
对于短 shunt 发电机:
$${\mathrm{\mathrm{电枢电流,}\mathit{I_{a}}\:=\:\mathit{I_{L}+I_{sh}}}}$$
$${\mathrm{\mathrm{串励磁电流,}\mathit{I_{se}}\:=\:\mathit{I_{L}}}}$$
$${\mathrm{\mathrm{并励磁电流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{t}}+\mathit{I_{se}R_{se}}}{R_{sh}}}}$$
$${\mathrm{\mathrm{端电压,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}R_{a}-I_{se}R_{se}}}}$$
对于长 shunt 发电机:
$${\mathrm{\mathrm{电枢电流,}\mathit{I_{a}}\:=\:\mathit{I_{L}+I_{sh}}}}$$
$${\mathrm{\mathrm{串励磁电流,}\mathit{I_{se}}\:=\:\mathit{I_{a}}}}$$
$${\mathrm{\mathrm{并励磁电流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{t}}}{\mathit{R_{sh}}}}}$$
$${\mathrm{\mathrm{端电压,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}}\left ( \mathit{R_{a}+R_{se}} \right )}}$$
直流电机的原理
直流发电机的运行原理基于法拉第电磁感应定律。根据该定律,当穿过导体或线圈的磁通量发生变化时,导体或线圈中就会感应出电动势。该感应电动势的大小由下式给出:
$${\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\:\cdot \cdot \cdot (1)}}$$
其中,$\phi$是线圈的磁通链,N是线圈的匝数。
在直流发电机的情况下,磁通量 ($\phi$) 保持静止,线圈旋转。线圈旋转而磁通静止时感应的电动势称为动态感应电动势。

为了理解直流发电机的运行原理,我们考虑一个单环直流发电机(即 *N = 1*),如图所示。(此处应插入图示) 此处,线圈由某个原动机(机械能的来源)旋转,并且线圈的磁通链发生变化。
设 $\phi$ 为电机每个磁极产生的平均磁通量,则发电机中的平均感应电动势由下式给出:
$${\mathrm{\mathit{E_{av}}\:=\:\frac{\mathit{d\phi }}{\mathit{dt}}\:=\:\mathrm{线圈每秒切割的磁通量}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{一次旋转切割的磁通量\:\times \:每秒旋转次数}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{\left ( 每极磁通量\times 极数 \right )}\:\times \:\mathrm{每秒旋转次数}}}$$
$${\mathrm{\therefore \mathit{E_{av}}\:=\:\mathit{\phi \:\times P\:\times \:n}\:\cdot \cdot \cdot (2)}}$$
其中,*P* 是发电机的总极数,*n* 是线圈的每秒旋转速度。公式(2)给出了单环直流发电机中的平均感应电动势。
以下几点解释了直流发电机的运行原理:
位置1 - 感应电动势为零,因为线圈边的运动与磁通量平行。
位置2 - 线圈边与磁通量成一定角度运动,因此在环路中产生较小的电动势。
位置3 - 线圈边与磁通量成直角运动,因此感应电动势最大。
位置4 - 线圈边以一定角度切割磁通量,因此在线圈边中感应出较小的电动势。
位置5 - 线圈边没有与磁通量发生链结,并且线圈边与磁通量平行移动。因此,在线圈中没有感应电动势。
位置6 - 线圈边在相反极性磁极下移动,因此感应电动势的极性反转。最大电动势将在此方向上在位置7感应,而在位置1时为零。这个循环随着线圈的旋转而重复。
这样,就在直流发电机中感应出电动势。尽管这种感应电动势本质上是交流电,但随后可以使用称为换向器的装置将其转换为单向电动势。
直流发电机电枢导体中感应电动势的方向由弗莱明右手定则 (FRHR) 决定,我们在本教程的 *模块 1(基本概念)* 中讨论过。
直流电机中的反电动势
在直流电动机中,当电枢在驱动转矩的作用下旋转时,电枢导体穿过磁场,因此由于发电机作用会在其中感应出电动势。电枢导体中感应的这种电动势与施加电压$\mathit{V_{s}}$方向相反,被称为反电动势或逆电动势。
反电动势的大小由下式给出:
$$\mathrm{\mathit{E_{b}}\:=\:\frac{\mathit{NP\phi Z}}{\mathrm{60}\mathit{A}}\:\cdot \cdot \cdot (1)}$$
反电动势$\mathit{E_{b}}$总是小于施加电压$\mathit{V_{s}}$。但是,当直流电动机在正常条件下运行时,这种差异很小。
在直流电动机中,电枢中感应的反电动势$\mathit{E_{b}}$与施加电压相反,因此施加电压必须克服这个电动势$\mathit{E_{b}}$才能迫使电流$\mathit{I_{a}}$流过电枢电路以实现电机动作。克服这种阻力的所需功率由下式给出:
$$\mathrm{\mathit{P_{m}}\:=\:\mathit{E_{b}I_{a}}\:\cdot \cdot \cdot (2)}$$
功率$\mathit{P_{m}}$是实际转换为机械功率的部分。因此,功率$\mathit{P_{m}}$也称为机械功率的电等效值。
考虑一个其等效电路如图1所示的并励直流电动机。
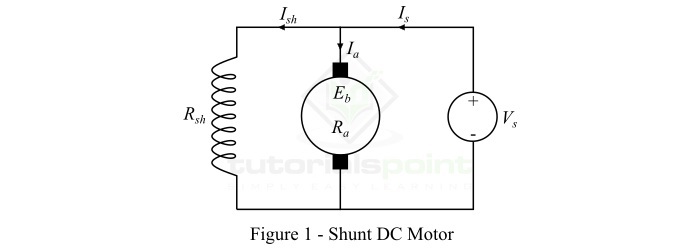
当在电动机的端子上施加直流电压$\mathit{V_{s}}$时,励磁电磁铁被励磁,电枢导体被供电。因此,驱动转矩作用于电枢,电枢开始旋转。当电枢旋转时,在电枢导体中感应出反电动势,该反电动势与施加电压$\mathit{V_{s}}$相反。施加电压必须克服反电动势使电流流过电枢导体。
直流电动机的电压方程可以表示为:
$$\mathrm{\mathit{V_{s}\:=\:E_{b}+I_{a}R_{a}}\:\cdot \cdot \cdot (3)}$$
其中,$\mathit{R_{a}}$是电枢电路的电阻。
那么,直流电动机的电枢电流由下式给出:
$$\mathrm{\mathit{I_{a}}\:=\:\frac{\mathit{V_{s}-E_{b}}}{\mathit{R_{a}}}\:\cdot \cdot \cdot (4)}$$
由于对于给定的电机,施加电压$\mathit{V_{s}}$和电枢电阻$\mathit{R_{a}}$通常是固定的,因此$\mathit{E_{b}}$的值将决定直流电动机吸收的电流。如果直流电动机的速度很高,则反电动势的值很大,因此电动机将吸收较少的电枢电流,反之亦然。
直流电动机中反电动势的重要性
直流电动机中的反电动势使其成为一台自调节电机,这意味着它使电动机能够吸收足够的电枢电流来产生机械负载所需的转矩。
现在,从公式(4)中,我们可以解释反电动势在直流电动机中的重要性如下:
情况1 - 电机空载运行
在这种情况下,直流电动机需要一个小的转矩来克服摩擦和风阻损失。因此,电动机吸收的电枢电流$\mathit{I_{a}}$很小,反电动势几乎等于电源电压。
情况2 - 电机负载突然变化
在这种情况下,当负载突然连接到电机轴上时,电枢会减速。因此,电枢导体穿过磁场的速度降低,因此反电动势降低。降低的反电动势允许更大的电流通过电枢导体,更大的电枢电流意味着更大的驱动转矩。因此,很明显,驱动转矩随着电机速度的降低而增加。当电枢电流足以产生机械负载所需的增加的转矩时,电机速度的降低停止。
考虑另一种情况,其中电机的负载减小。在这种情况下,驱动转矩暂时大于需求,因此电枢被加速。电枢速度的增加增加了反电动势,并导致电枢电流减小。一旦电枢电流足以产生负载所需的降低的驱动转矩,电机将停止加速。
这段讨论清楚地表明,直流电动机中的反电动势会自动调节电枢电流的流动以满足负载要求。
直流电机的类型
在实际的直流电动机中,磁场是由电磁铁而不是永磁体产生的。然后根据励磁绕组在电机电路中的连接方式对直流电动机进行分类。在此基础上,直流电动机分为以下两种类型:
他励直流电动机
自励直流电动机
他励直流电动机
磁场绕组由独立的直流电源(如电池)励磁的直流电动机称为他励直流电动机。图1显示了自励直流电动机的连接图。
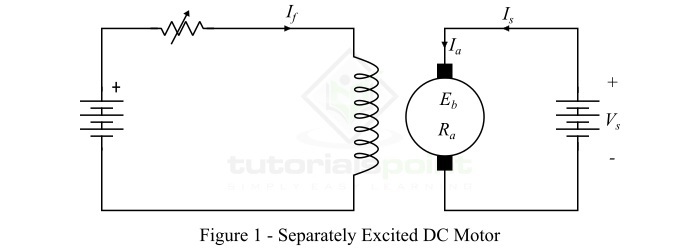
他励直流电动机的速度取决于电源电压和励磁电流,即电机中的磁通量。但是,他励直流电动机很少用于实际应用中,因为它们需要外部直流电源进行励磁。
自励直流电动机
磁场绕组由与电枢供电相同的电源励磁的直流电动机称为自励直流电动机。
根据磁场绕组与电枢绕组的连接方式,自励直流电动机分为以下三种类型:
串励直流电动机
并励直流电动机
复励直流电动机
串励直流电动机
磁场绕组与电枢绕组串联,使整个电枢电流流过磁场绕组的直流电动机称为串励直流电动机。图2显示了串励直流电动机的连接图。
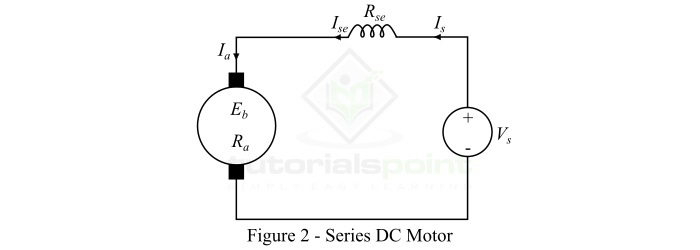
对于串励直流电动机,磁场绕组承载整个电枢电流,因此它由较粗的线圈和较少的匝数组成,以便具有最小的电阻。
以下是串励直流电动机的一些重要表达式:
$$\mathrm{\mathrm{电枢电流},\mathit{I_{a}}\:=\:\mathit{I_{se}}\:=\:\mathit{I_{s}}}$$
其中,$\mathit{I_{se}}$是串励磁电流,$\mathit{I_{s}}$是电源电流。
$$\mathrm{\mathrm{电源电压},\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}\left ( \mathit{R_{a}+R_{se}} \right )}}$$
其中,$\mathit{E_{b}}$是反电动势,$\mathit{R_{a}}$是电枢电路电阻,$\mathit{R_{se}}$是串励磁电阻。
并励直流电动机
磁场绕组与电枢绕组并联,使总电源电压施加在其上的直流电动机称为并励直流电动机。图3显示了并励直流电动机的连接图。
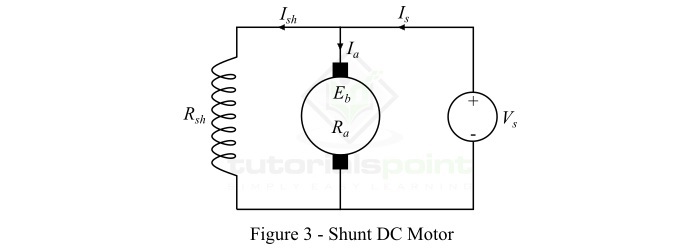
在并励直流电动机中,并励磁绕组具有大量细线圈,因此电阻很大,因此只有一部分电源电流流过它,其余部分流过电枢绕组。
以下是并励直流电动机的重要表达式:
$$\mathrm{\mathrm{电枢电流,}\mathit{I_{a}}\:=\:\mathit{I_{s}-I_{sh}}}$$
$$\mathrm{\mathrm{并励磁电流,}\mathit{I_{sh}}\:=\:\mathit{\frac{V_{s}}{R_{sh}}}}$$
$$\mathrm{\mathrm{电源电压,}\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}R_{a}}}$$
复励直流电动机
复励直流电动机是指在每个磁极上都有两组磁场绕组的电动机——一个与电枢绕组串联,另一个与电枢绕组并联。
复励直流电动机细分为以下两种类型:
短 shunt 复励直流电动机
长 shunt 复励直流电动机
短 shunt 复励直流电动机是指只有并励磁绕组与电枢绕组并联的电动机,如图4所示。
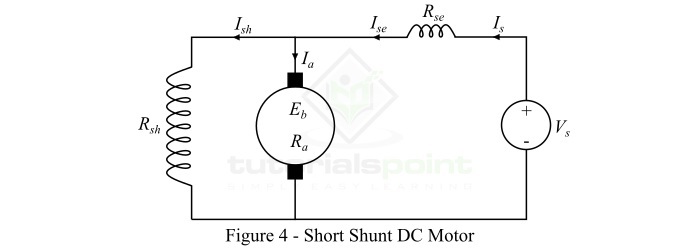
长 shunt 复励直流电动机是指并励磁绕组与串励磁绕组和电枢绕组都并联的电动机,如图5所示。
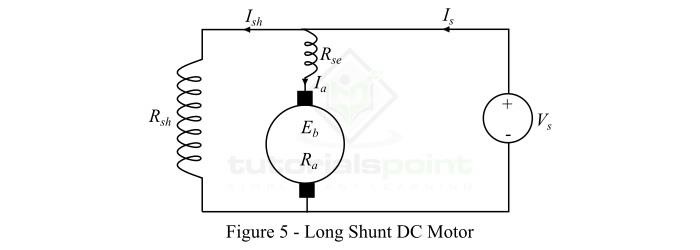
以下是复励直流电动机的重要表达式:
对于短 shunt 电机,
$$\mathrm{\mathrm{电枢电流,}\mathit{I_{a}}\:=\:\mathit{I_{s}-I_{sh}}}$$
$${\mathrm{\mathrm{串励磁电流,}\mathit{I_{se}}\:=\:\mathit{I_{a}}}}$$
$$\mathrm{\mathrm{并励磁电流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{s}}-\mathit{I_{se}R_{se}}}{R_{sh}}}$$
$$\mathrm{\mathrm{电源电压},\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}R_{a}+I_{se}R_{se}}}$$
对于长 shunt 电机,
$$\mathrm{\mathrm{电枢电流,}\mathit{I_{a}}\:=\:\mathit{I_{s}-I_{sh}}}$$
$$\mathrm{\mathrm{串励磁电流,}\mathit{I_{se}}\:=\:\mathit{I_{s}}}$$
$$\mathrm{\mathrm{并励磁电流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{s}}}{R_{sh}}}$$
$$\mathrm{\mathrm{电源电压},\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}\left ( R_{a}+R_{se} \right )}}$$
直流电机的损耗
在直流电机(发电机或电动机)中,损耗可分为三类,即:
铜损
铁损或铁芯损耗
机械损耗
所有这些损耗都以热量的形式出现,从而提高了机器的温度。它们还会降低机器的效率。
铜损
在直流电机中,由于电机各种绕组的电阻而发生的损耗称为铜损。铜损也称为I2R损耗,因为这些损耗是由于电流流过绕组的电阻而发生的。
直流电机中发生的 主要铜损如下:
$$\mathrm{\mathrm{电枢铜损}\:=\:\mathit{I_{a}^{\mathrm{2}}R_{a}}}$$
$$\mathrm{\mathrm{串励磁铜损}\:=\:\mathit{I_{se}^{\mathrm{2}}R_{se}}}$$
$$\mathrm{\mathrm{并励磁铜损}\:=\:\mathit{I_{sh}^{\mathrm{2}}R_{sh}}}$$
在直流电机中,由于电刷接触电阻,还会产生电刷接触损耗。在实际计算中,这种损耗通常包含在电枢铜损中。
铁损
铁损是由于电枢在磁场中旋转而在直流电机电枢铁芯中发生的。因为这些损耗发生在电枢铁芯中,所以也称为铁芯损耗。
铁损或铁芯损耗有两种类型,即磁滞损耗和涡流损耗。
磁滞损耗
当电枢在不同极性的连续磁极下通过时,由于电枢铁芯中的磁场反转而在直流电机电枢铁芯中发生的铁芯损耗称为磁滞损耗。磁滞损耗由以下经验公式给出:
$$\mathrm{\mathrm{磁滞损耗,}\mathit{P_{h}}\:=\:\mathit{k_{h}B_{max}^{\mathrm{1.6}}fV}}$$
其中,$\mathit{k_{h}}$是斯坦梅茨磁滞系数,$\mathit{B_{max}}$是最大磁通密度,f是磁场反转频率,V是电枢铁芯的体积。
可以通过使电枢铁芯采用斯坦梅茨磁滞系数较低的材料(如硅钢)来降低直流电机中的磁滞损耗。
涡流损耗
当直流电机电枢在磁极的磁场中旋转时,会在电枢铁心中感应出电动势,并在其中产生涡流。由于这些涡流引起的功率损耗称为**涡流损耗**。
$$ \mathrm{涡流损耗,} \mathit{P_{e}} = \mathit{k_{e}B_{max}^{2}f^{2}t^{2}V} $$
其中,$\mathit{K_{e}}$是比例常数,t是叠片厚度。
从涡流损耗的表达式可以看出,涡流损耗取决于叠片厚度的平方。因此,为了减少这种损耗,电枢铁心是由薄叠片构成,这些叠片之间用一层薄薄的清漆绝缘。
机械损耗
直流电机中由于摩擦和风阻引起的功率损耗称为**机械损耗**。在直流电机中,摩擦损耗以轴承摩擦、电刷摩擦等形式出现,而风阻损耗是由于旋转电枢的空气摩擦引起的。
机械损耗取决于电机的转速。但在给定转速下,这些损耗实际上是恒定的。
**注意**——铁损或铁芯损耗和机械损耗一起称为**杂散损耗**。
恒定损耗和可变损耗
在直流电机中,我们可以将上述讨论的损耗分为以下两类:
恒定损耗
可变损耗
直流电机中在所有负载下保持恒定的损耗称为**恒定损耗**。这些损耗包括:*铁损、励磁绕组铜损和机械损耗*。
直流电机中随负载变化的损耗称为**可变损耗**。直流电机的可变损耗包括:电枢铜损和串励绕组铜损。
Total losses in a DC machine = Constant losses + Variable losses
直流电机的应用
目前,大量的电能以交流电的形式产生。因此,直流电机(电动机或发电机)的使用变得有限。然而,直流电机仍在一些应用中使用,例如为交流发电机的励磁系统供电、电解过程、焊接过程等。
直流发电机的应用
不同类型直流发电机的应用如下:
他励直流发电机
发电机主要用于实验室的实验和测试。
它们也用作为直流电动机供电的直流电源。
串励直流发电机
串励直流发电机用于直流机车再生制动,为励磁电流供电。
串励直流发电机也用作配电系统中的升压器。
差动复励串励发电机用于电弧焊接。
过励磁积性串励发电机用于照明和重型电源。
平励串励发电机用于为办公室、住宅和其他商业建筑供电。
并励直流发电机
shunt 直流发电机主要用于照明。
shunt 直流发电机用于充电电池。
这些发电机也用于为交流发电机供给励磁电流。
直流电动机的应用
不同类型直流电动机的应用如下:
串励直流电动机
串励直流电动机用于需要高启动转矩的应用。
串励直流电动机用于起重机和升降机。
串励直流电动机用于电力牵引。
它们用于空气压缩机。
它们也用于真空吸尘器。
串励直流电动机也用于缝纫机等。
并励直流电动机
shunt 直流电动机用于需要恒速的应用。
shunt 直流电动机用于驱动车床。
它们也用于离心泵和鼓风机。
它们用于风扇、输送机和纺纱机。
这些直流电动机也用于电梯。
复励直流电动机
复励直流电动机用于那些需要高启动转矩和恒速的应用。
用于印刷机。
它们也用于剪切机。
它们用于电梯和升降机。
复励直流电动机也用于轧机和重型刨床等。
感应电机的介绍
**感应电动机**是工业应用中最广泛使用的电动机。几乎所有感应电动机从空载到满载条件下都以基本恒定的速度运行。感应电动机的速度取决于电源频率,因此这些电动机不容易适应速度控制。感应电动机的结构简单而坚固,价格便宜,易于维护,并且可以设计和生产出具有满足大多数工业要求的特性。
什么是感应电动机?
**感应电动机**是一种异步交流电动机,它将交流电转换成机械能。它被称为感应电动机,因为产生驱动转矩所需的转子电路中的电流是通过定子绕组的旋转磁场进行**电磁感应**获得的。
这些电动机被称为异步电动机,因为它们的转子转速低于旋转磁场的同步转速。

感应电动机是一种机电能量转换装置,即它将电能转换成机械能,以轴的旋转形式出现。像任何电动机一样,感应电动机有两个主要部分,即**定子**和**转子**。
定子带有一组称为**定子绕组**的绕组。定子绕组可以是单相绕组或三相绕组。
转子带有一个短路绕组,称为**转子绕组**。
在感应电动机中,只有定子绕组由交流电源供电,而转子绕组通过电磁感应从定子绕组获得电压和功率。
感应电动机的运行原理
感应电动机的运行基于**电磁感应原理**。在感应电动机中,有两个绕组,即 *定子绕组和转子绕组*。输入交流电源连接到定子绕组,流过定子绕组的电流产生磁通。这个磁通通常是旋转的,因此也称为旋转磁场。感应电动机的转子绕组是一个短路绕组。
来自定子的旋转磁通切割转子绕组的短路导体。根据法拉第电磁感应定律,在转子电路中感应出电动势,导致电流流过它。当电流流过转子绕组时,机器中会产生另一个磁通。
因此,感应电动机内部有两个磁通,一个是定子磁通,另一个是转子磁通。这两个磁通相互作用。正因为如此,转子将受到一个转矩,使转子沿定子旋转磁场的方向旋转。就这样,感应电动机运行。
感应电动机的类型
根据输入电源的类型,感应电动机分为以下两种类型:
**单相感应电动机**——在单相交流电源下工作的感应电动机称为单相感应电动机。
**三相感应电动机**——需要三相交流电源才能运行的感应电动机称为三相感应电动机。
感应电动机的优点
以下是感应电动机的一些主要优点:
感应电动机的结构简单而坚固。
感应电动机的价格相对便宜。
感应电动机的效率相对较高。
感应电动机可以设计成具有满足工业要求的特性。
感应电动机几乎不需要维护。
感应电动机的缺点
感应电动机的主要缺点如下:
感应电动机的速度不容易改变,因为它们基本上是恒速电动机。
感应电动机在启动时会吸收很大的涌流。
感应电动机始终在滞后功率因数下运行。
单相感应电动机不是自启动的;因此,我们需要提供一些额外的启动机构。
单相感应电机
顾名思义,这些感应电动机是在单相交流电源上运行的。**单相感应电动机**是最常见的电动机,因为它们通常用于家用和商用电器,如风扇、泵、洗衣机、空调、冰箱等。
虽然单相感应电动机的效率比三相感应电动机低,但它们被广泛用作低功率应用中三相感应电动机的替代品。
典型的单相感应电动机由两个主要部分组成——*定子*和*转子*。单相感应电动机的定子带有单相绕组,而转子采用鼠笼式结构。
如何使感应电动机自启动?
单相感应电动机的主要缺点是它不是自启动的,而是需要某种启动机构。在单相感应电动机中,定子绕组产生一个以正弦方式变化的脉动磁场。因此,该磁场在交流电的每个半周期后都会反转其极性,但在空间中不会旋转。结果,这个交变磁场不会在静止转子中产生旋转。虽然,如果转子通过某种外部手段在一个方向上旋转,它将继续沿旋转方向运行。然而,这种启动单相感应电动机的方法在实践中并不方便。
因此,为了使单相感应电动机自启动,我们需要以某种方式在电机内部产生旋转磁场。这可以通过提供一个附加绕组将单相交流电源转换为两相交流电源来实现。因此,单相感应电动机在其定子上包含两个绕组,即**主绕组**和**启动绕组**。这两个绕组彼此相差90°。
单相感应电动机的类型
根据电机自启动方式的不同,单相感应电动机可分为以下三种类型:
分相式感应电动机
电容启动式感应电动机
电容启动电容运行式感应电动机
现在让我们更详细地讨论每种感应电动机。
分相式感应电动机
分相式感应电动机是一种单相感应电动机,其定子由两个绕组组成,即启动绕组和主绕组,其中启动绕组相对于主绕组电角度上相差90°。
启动绕组仅在电机启动期间工作。启动绕组和主绕组的设计使得启动绕组具有高电阻和相对低的电抗,而主绕组具有相对低的电阻和高电抗,以便两个绕组中流动的电流具有大约25°到30°的合理相位差($\alpha$)。
现在,当电机的启动绕组连接到单相交流电源时,启动绕组将承载电流$\mathit{I_{s}}$,而主绕组将承载电流$\mathit{I_{m}}$,如图1所示。
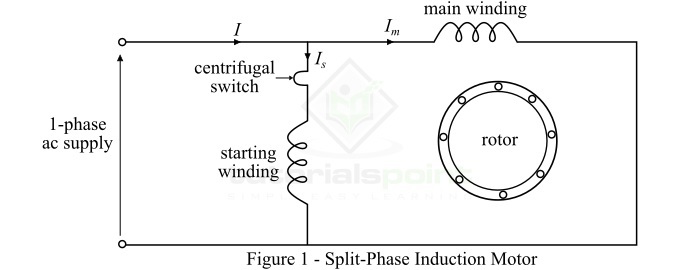
由于启动绕组设计成高电阻,而主绕组设计成高电感。因此,两个绕组中的电流$\mathit{I_{s}}$和$\mathit{I_{m}}$具有大约25°到30°的合理相位差。结果,在电机内部产生一个较弱的旋转磁场,从而启动电机。
电容启动式感应电动机
这种类型的单相感应电动机,如图2所示,在启动绕组串联连接一个电容C。这个电容称为启动电容。启动电容的值选择使得启动电流$\mathit{I_{s}}$领先于通过主绕组的电流$\mathit{I_{m}}$约80°。
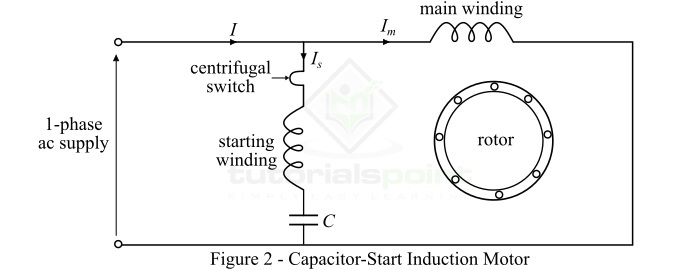
一旦电机达到额定速度的约75%,离心开关就会将启动绕组与电路隔离。然后,电机作为单相感应电动机运行,并继续加速直到达到正常速度。因此,在这种类型的单相感应电动机中,启动绕组串联的电容会在两个绕组之间引入相移,以便电机能够自行启动。
电容启动电容运行式感应电动机
这种电机与电容启动式感应电动机几乎相同,只是启动绕组不会与电机电路断开。因此,对于电容启动电容运行式感应电动机,启动和运行期间,两个绕组(启动绕组和主绕组)都保持连接到电源。
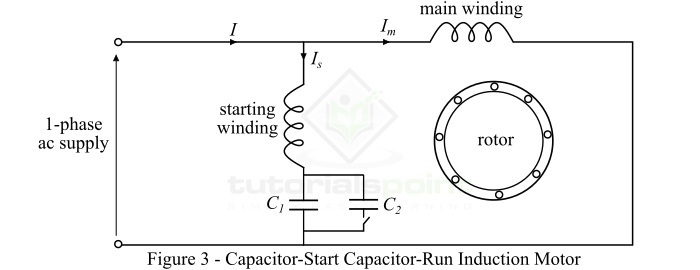
在这种电机中,启动绕组使用两个电容C1和C2,如图3所示。电容C1具有较小的电容值,用于电机的最佳运行,因此永久地与启动绕组串联连接,而较大的电容C2与C1并联连接,并且它仅在启动期间保持在电路中。当电机达到额定速度的约75%时,离心开关将启动电容C2与电路隔离。然后电机作为单相感应电动机运行。
单相感应电机的应用
单相感应电动机主要用于家用和商用电器,如风扇、空调、冰箱、空气冷却器、洗衣机等。以下是各种单相感应电动机的一些应用:
分相式感应电动机——这些电机最适合中等启动转矩的应用,例如风扇、洗衣机、燃油燃烧器、小型机床等。
电容启动式感应电动机——这些电机适用于需要相对较高的启动转矩的应用,例如压缩机、大型风扇、泵和高惯性负载等。
电容启动电容运行式感应电动机——这些电机适用于恒转矩和无振动的应用,例如医院设备、录音棚设备以及许多其他需要安静运行的设备。
三相感应电机
顾名思义,三相感应电动机是一种使用三相交流电源工作的电动机,它将三相交流电转换为机械能。三相感应电动机是工业中最广泛使用的电动机。这些电机的速度从空载到满载几乎恒定,即它们具有良好的调速性能。虽然三相感应电机的速度取决于电源频率和电机中的极数,因此很难改变其速度。
与任何其他电动机一样,典型的三相感应电动机也由两个主要部分组成,即定子和转子。定子是静止部分,并带有三相绕组,称为定子绕组。转子是电机的旋转部分,并带有短路绕组,称为转子绕组。
三相感应电机的定子绕组由三相平衡交流电源供电,而转子绕组通过电磁感应从定子绕组获得工作电压和功率。这就是它被如此命名的原因。
三相感应电动机可以被认为是具有旋转次级绕组的三相变压器。因此,它可以被描述为一种变压器型交流电机。唯一的区别在于感应电动机将电能转换为机械能。
三相感应电机的类型
根据转子结构的不同,三相感应电动机可分为以下两种基本类型:
鼠笼式感应电动机
滑环式感应电动机
三相感应电机的优点
以下是三相感应电动机的一些主要优点:
三相感应电机的设计和制造非常简单。
它们具有坚固的结构。
三相感应电动机需要较少的维护。
三相感应电动机具有自启动特性。
这些电机具有相当好的功率因数。
三相感应电动机更经济。
它们具有高效率。
三相感应电机的缺点
三相感应电机的主要缺点如下:
三相感应电动机基本上是恒速电机,需要复杂的机构来改变速度。
三相感应电动机始终工作在滞后功率因数下。
这些电机启动电流非常高。
三相感应电机的应用
三相感应电机的主要应用如下:
鼠笼式三相感应电动机适用于驱动鼓风机、风扇、机床、离心泵等。
三相感应电动机也用于驱动不同的工业负载,如压缩机、破碎机、输送机、往复泵等。
滑环式感应电动机最适合驱动需要高启动转矩的负载,如破碎机、柱塞、起重机、电梯、提升机、输送机等。
三相感应电机的构造
三相感应电动机由两个主要部分组成,即:
定子
转子
定子和转子之间有一个小的气隙,其范围为0.4毫米到4毫米,具体取决于电机的额定功率。
定子
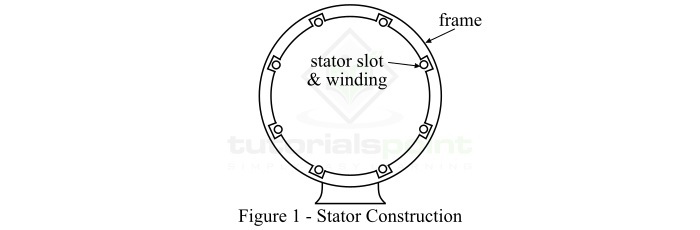
三相感应电机的定子是静止部分,它由一个由钢板制成的圆柱形框架组成。这个钢制框架封闭着一个由硅钢薄叠片组成的空心圆柱形铁芯。在铁芯的内周,设置了许多均匀间隔的槽,用于放置定子绕组。硅钢叠片用于减少磁滞和涡流损耗。
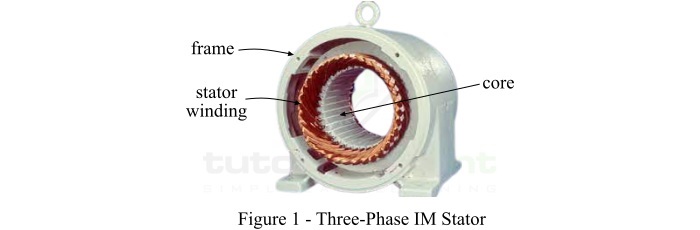
三个绕组放置在定子槽中,并适当地连接以形成平衡的三相三角形或星形连接电路。根据电机速度的要求,这三个绕组绕制成一定的极数。其中,极数越多,感应电机的速度越低,反之亦然。
当我们用平衡的三相电源供电给三相定子绕组时,就会产生一个幅值恒定的旋转磁场。这个旋转磁场通过电磁感应在转子电路中感应电动势。
转子
转子是三相感应电机的旋转或移动部分。它由一个由优质硅钢薄叠片制成的转子铁芯组成,以减少磁滞和涡流损耗。转子铁芯是一个空心圆柱体,安装在轴上。在转子铁芯的外周,设置了槽,用于放置转子绕组。
根据结构的不同,三相感应电机的转子可以是以下两种类型:
鼠笼式转子
绕线式转子
让我们详细讨论这两种类型的转子。
鼠笼式转子
鼠笼式转子由一个叠片圆柱形铁芯组成,其外周具有平行槽。对于鼠笼式转子,转子绕组由金属(铜或铝)条组成。这些金属条放置在转子槽中,并在每端由称为端环的金属环短路,如图2所示。

从图2可以看出,这种转子的结构类似于松鼠笼,因此得名。这里还要注意的是,转子没有与电源电连接,而是通过电磁感应从定子获得电压和功率。
采用鼠笼式转子的三相感应电动机被称为鼠笼式感应电动机。由于其简单而坚固的结构使其能够在大多数恶劣环境下运行,因此在工业应用中使用的三相感应电动机中,有70%到80%是鼠笼式感应电动机。尽管使用鼠笼式转子的感应电动机启动转矩较低。
绕线式转子
绕线式转子由一个由硅钢制成的叠片圆柱形铁芯组成。它带有类似于定子绕组的三相转子绕组,如图3所示。
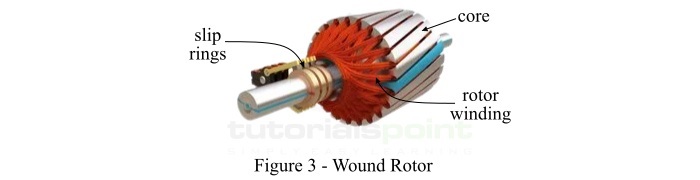
绕线式转子的转子绕组均匀地分布在槽中,并以星形方式连接。星形连接的转子绕组的开口端被引出并连接到安装在转子轴上的三个滑环。一个碳刷接触在每个滑环上,并且通过这些碳刷,可以将外部电阻添加到转子电路中。
启动时,在转子绕组的各相中加入合适的外部电阻,以获得较高的启动转矩。随着电动机加速到额定速度,这些外部电阻会逐渐从电路中移除。使用外部电阻可以显著降低启动电流并提高电动机的启动转矩。一旦电动机达到正常速度,三个碳刷短路,使绕线式电动机像鼠笼式感应电动机一样运行。
三相感应电机负载运行
本章将解释三相异步电动机带负载时的运行特性。
当我们将机械负载连接到三相异步电动机的转子轴上时,转子将开始减速,因此旋转磁场 (RMF) 将以更高的速率切割转子导体。因此,转子导体中的感应电动势和电流将逐渐增加,产生更大的转矩。此转矩加速转子,转子和机械负载很快就会达到平衡状态,此时转子转矩和负载转矩相等。一旦达到此状态,电动机的速度停止进一步下降,因此电动机将以新的速度匀速运行。
然而,三相异步电动机随着负载增加而速度下降的幅度很小。这是因为其转子电路的阻抗很低,速度的微小下降会产生较大的转子电流。这种增加的转子电流产生更大的转矩,以满足电动机轴上增加的负载需求。这就是为什么三相异步电动机被认为是恒速电动机的原因。但是,这些电动机永远不会以同步速度运行,因此它们也称为异步电动机。
从技术上讲,三相异步电动机的负载变化是通过调整滑差 (同步速度和转子速度之差) 来实现的。这意味着,随着电动机轴上负载的增加,滑差会略微增加。因此,旋转磁场和转子导体之间的相对速度增加。因此,转子电流增加,产生更大的电动机转矩以满足增加的负载需求。
此外,随着机械负载的增加,增加的转子电流的方向会降低定子的旋转磁通 (根据楞次定律),从而降低定子绕组的反电动势。反电动势的降低允许定子电流增加,从而增加感应电动机的输入功率。
感应电动机的滑差概念
在三相异步电动机中,转子永远无法达到定子旋转磁场的速度 (称为同步速度)。如果达到同步速度,旋转磁场和转子导体之间就不会有相对运动,转子导体中就不会有感应电动势,因此也就没有转矩来旋转转子。因此,实际上,感应电动机的转子速度总是小于同步速度。这种差异称为滑差速度,即:
$$ \mathrm{滑差速度} = N_{s} - N_{r} $$
其中,$N_{s}$ 是同步速度,$N_{r}$ 是转子速度。
$$ \mathrm{同步速度,} N_{s} = \frac{120f}{P} $$
其中,f 是电源频率,P 是感应电动机的极数。
滑差速度与同步速度的比率称为感应电动机的滑差,即:
$$ \mathrm{滑差,} s = \frac{N_{s} - N_{r}}{N_{s}} $$
此外,
$$ \mathrm{滑差百分比,} s = \frac{N_{s} - N_{r}}{N_{s}} \times 100\% $$
在实际的三相异步电动机中,从空载到满载的滑差变化约为 0.1% 到 3%。
数值例子
一个 8 极 3 相感应电动机连接到 60 Hz 电源。如果它以 880 RPM 的速度运行。计算滑差。
解答
已知数据:
极数,P = 8
频率,f = 60 Hz
转子速度,Nr = 880 RPM
$$ \mathrm{因此同步速度,} N_{s} = \frac{120 \times 60}{8} = 900 $$
因此,滑差为:
$$ \mathrm{滑差,} s = \frac{900 - 880}{900} \times 100 = 2.22\% $$
三相感应电机的特性
三相异步电动机的运行性能可以用以下两个特性来解释:
转矩-滑差特性
转矩-速度特性
三相异步电动机的转矩-滑差特性
三相异步电动机的转矩-滑差特性是在特定转子电阻值下,电动机转矩与滑差之间绘制的曲线。图 1 显示了典型三相异步电动机的不同转矩-滑差特性,滑差范围为 s = 0 到 s = 1,转子电阻值为各种不同的值。
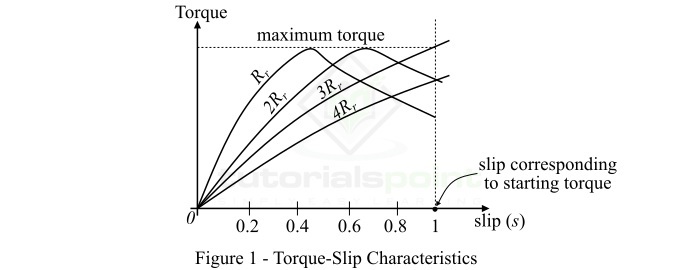
对于三相异步电动机,运行条件下电动机转矩与滑差之间的关系由下式给出:
$$ \tau_{r} = \frac{KsR_{r}}{R_{r}^{2} + s^{2}X_{r}^{2}} \cdots (1) $$
其中,K 是常数,s 是滑差,$R_{r}$ 是每相转子电阻,$X_{r}$ 是每相静止转子电抗。
从公式 (1) 中,我们可以得出以下几点:
情况 1
如果 s = 0,则 $\tau_{r} = 0$。因此,转矩-滑差曲线从原点开始。
情况 2
在电动机的正常速度下,滑差很小,因此 $sX_{r}$ 与 $R_{r}$ 相比实际上可以忽略不计。
$$ \tau_{r} \propto \frac{s}{R_{r}} $$
由于对于给定的电动机,$R_{r}$ 也是常数。
$$ \tau_{r} \propto s $$
因此,转矩-滑差曲线是从零滑差到对应于满载滑差的直线。
情况 3
如果滑差值超过满载滑差,则转矩增加并在 $R_{r} = sX_{r}$ 时达到最大值。三相异步电动机中的这个最大转矩称为击穿转矩或最大转矩。当感应电动机在额定电压和频率下运行时,击穿转矩的值至少是满载转矩的两倍。
情况 4
当滑差值大于对应于最大转矩的滑差值时,$s^{2}X_{r}^{2}$ 项迅速增加,因此可以忽略 $R_{r}^{2}$。
$$ \tau_{r} \propto \frac{s}{s^{2}X_{r}^{2}} $$
由于 $X_{r}^{2}$ 实际上是常数,则
$$ \tau_{r} \propto \frac{1}{s} $$
因此,转矩现在与滑差成反比。因此,转矩-滑差曲线是矩形双曲线。
因此,从以上对三相异步电动机转矩-滑差特性的分析可以看出,向转子电路中添加电阻不会改变最大转矩的值,而只会改变发生最大转矩的滑差值。
三相异步电动机的转矩-速度特性
对于三相异步电动机,电动机转矩取决于速度,但我们无法用简单的数学方程来表示它们之间的关系。因此,我们使用转矩-速度特性曲线来显示这种关系。图 2 显示了三相异步电动机的典型转矩-速度特性曲线。
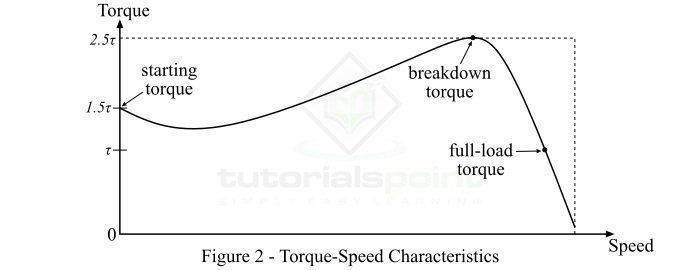
从该特性曲线中可以注意到以下几点:
如果满载转矩为 $\tau$,则启动转矩为 $1.5\tau$,最大转矩(或击穿转矩)为 $2.5\tau$
在满载情况下,如果电动机的速度为 N,如果轴上的机械负载增加,则电动机的速度将下降,直到电动机转矩再次等于负载转矩。一旦两个转矩相等,电动机将以恒定速度运行,但低于之前的速度。但是,如果电动机转矩大于 $2.5\tau$(即击穿转矩),则电动机将突然停止。
对于三相异步电动机,转矩-速度曲线在空载点和满载点之间基本上是一条直线。曲线线的斜率取决于转子电路的电阻,即电阻越大,斜率越陡峭。
调速和速度控制
感应电动机的速度调节
感应电动机的速度调节定义为电动机速度随负载变化而变化的程度。它表示为满载速度的分数或百分比,即:
$$ \mathrm{速度调节} = \frac{N_{nl} - N_{fl}}{N_{fl}} \times 100\% $$
其中,$N_{nl}$ 是电动机的空载速度,$N_{fl}$ 是电动机的满载速度。
感应电动机的速度调节约为 3% 到 5%。由于这种小的速度调节,感应电动机被归类为恒速电动机。
三相异步电动机的速度控制
三相异步电动机的速度由下式给出:
$$ N_{r} = (1 - s)N_{s} \cdots (1) $$
其中,s 是滑差,$N_{s}$ 是以 RPM 表示的同步速度。
$$ N_{s} = \frac{120f}{P} \cdots (2) $$
从公式 (1) 和 (2) 可以看出,可以通过改变以下参数来改变三相异步电动机的速度:
交流电源的频率 (f),
定子极数 (P),以及
滑差 (s)。
实际上,通常无法改变电源频率,因为商用电力供应的频率是恒定的。因此,可以通过改变定子极数 (P) 或滑差 (s) 来改变三相异步电动机的速度。我们现在将讨论鼠笼式和滑环式感应电动机的速度控制。
鼠笼式感应电动机的速度控制
鼠笼式感应电动机的速度控制是通过改变定子极数来改变的。通过改变极数的方法,只有两种或四种速度是可能的。
在两速感应电动机中,提供一个定子绕组,可以通过合适的控制设备进行切换以提供两种速度。其中一种速度是另一种速度的一半。例如,定子绕组可以连接到 4 个或 8 个定子极,当电动机由 50 Hz 交流电源供电时,同步速度分别为 1500 RPM 和 750 RPM。
在四速感应电动机中,提供两个独立的定子绕组,每个绕组提供两种速度。
以下是改变极数速度控制方法的主要缺点:
此方法不能用于获得逐渐连续的速度控制。
它使电动机的设计和定子绕组互连的切换更加复杂。
由于设计和互连的复杂性,此方法最多只能为任何一台电动机提供四种不同的速度。
滑环式感应电动机的速度控制
可以通过改变电动机滑差来改变滑环式感应电动机的速度。采用以下方法来改变滑差,从而改变速度:
通过改变定子线电压。
通过改变转子电路的电阻。
通过在转子电路中添加和改变外加电压。
数值例子
对于三相异步电动机,电动机的空载速度为 900 RPM,满载速度为 880 RPM。求电动机的速度调节。
解答
已知数据:
$N_{nl}$ = 900 RPM
$N_{fl}$ = 880 RPM
$$ \mathrm{速度调节} = \frac{N_{nl} - N_{fl}}{N_{fl}} \times 100\% $$
$$ \mathrm{速度调节} = \frac{900 - 880}{880} \times 100\% = 2.273\% $$
三相感应电机的启动方法
以下四种方法广泛用于启动三相异步电动机:
直启动器
自耦变压器启动器
星-三角启动器
转子电阻启动器
本章将详细讨论每种启动方法。
直启动器
顾名思义,直启动器 (D.O.L.) 指的是将三相感应电动机直接连接到三相平衡交流电源上启动的方法,如图 1 所示。
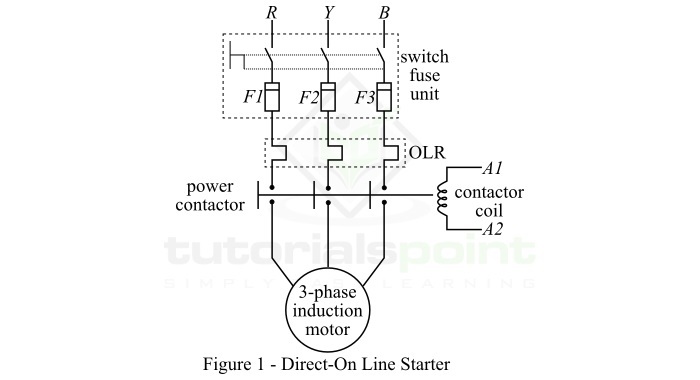
在这种方法中,感应电动机将吸收非常高的启动电流,大约是额定电流的 4 到 10 倍。这是因为电动机静止时的阻抗很低。因此,直启动 (D.O.L.) 方法适用于低功率等级的电动机,通常功率等级不超过 7.5 kW。
自耦变压器启动器
在这种感应电动机启动方法中,使用三相自耦变压器向电动机提供三相电力。自耦变压器主要用于降低启动时的电源电压,然后在电动机达到足够的速度后将其连接到全电压电源。
自耦变压器启动器的电路布置如图 2 所示。用于启动感应电动机的自耦变压器上的抽头设置方式为:当它连接到电路中时,向电动机施加 60% 到 80% 的电源电压。
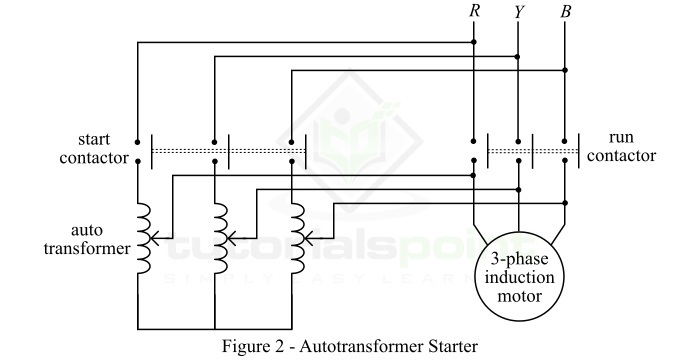
启动瞬间,自耦变压器接入电路,从而降低了施加到电动机的电压。因此,启动电流被限制在一个安全值内。当电动机达到额定速度的约 80% 时,通过转换开关将自耦变压器从电路中移除,然后将电动机连接到全电压电源。自耦变压器启动器具有功率损耗低、启动电流小等优点。因此,这种方法适用于功率等级超过 25 马力的较大感应电动机。
星-三角启动器
在这种方法中,三相感应电动机以星形连接方式启动,然后以三角形连接方式运行。
采用星-三角启动器的感应电动机的定子绕组设计为三角形运行,并在启动期间连接成星形。当电动机达到足够的速度时,绕组连接将从星形改为三角形。
图 3 显示了星-三角启动器的电路布置。这里,定子绕组的六个端子连接到一个转换开关。启动瞬间,转换开关将定子绕组连接成星形配置。结果,每个定子相位获得等于 *V/*√3 的电压,其中 *V* 是全线电压。这样,在启动期间,定子绕组获得降低的电压。
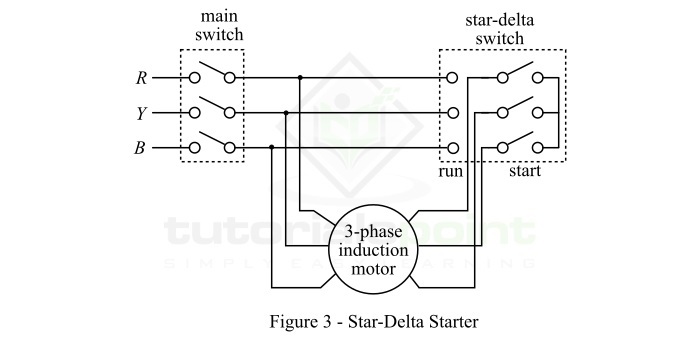
当电动机达到特定速度时,转换开关将定子绕组的连接改为三角形。每个相位现在获得全线电压 V,并且电动机以正常速度运行。然而,这种三相感应电动机的启动方法会导致电动机的启动转矩大幅降低。这种方法最适合中等尺寸的感应电动机,功率等级不超过约 25 马力。
转子电阻启动器
这种启动方法仅适用于滑环感应电动机。在这种方法中,一个可变星形连接的电阻器通过滑环插入转子电路,并将全电压施加到定子绕组。转子电阻启动器的电路布置如图 4 所示。
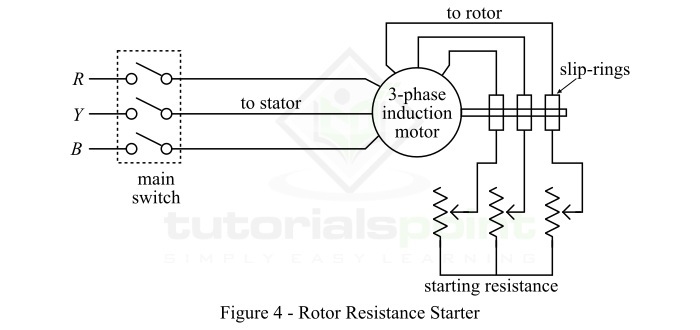
启动瞬间,星形连接电阻器的旋钮设置为“关闭”位置。因此,在转子电路的每个相位中插入最大电阻,从而降低启动电流。同时,该电阻会增加启动转矩。
当电动机加速时,通过移动电阻器旋钮,逐渐从转子电路中去除外部电阻。一旦电动机达到正常速度的约 80%,将旋钮切换到“开启”位置,从而将所有外部电阻从转子电路中移除。
三相同步电机的介绍
以同步速度(即旋转磁场的速度)运行的机电能量转换装置(或电机)被称为**同步电机**。同步电机是一种交流电机,即它需要交流电源才能工作。
根据能量转换,同步电机可分为两种类型:
同步发电机
同步电动机
同步电机是电力系统应用中使用最广泛的电机,例如发电机、功率因数校正、驱动恒速机械负载等。
将机械能转换为交流电的同步电机称为**同步发电机**或**交流发电机**。而将交流电转换为机械能的同步电机称为**同步电动机**。
在大多数实际应用中使用的同步电机是三相交流电机。然而,也存在单相同步电机,但它们仅用于特殊应用。
同步电机(发电机或电动机)始终以恒定的速度运行,称为同步速度。**同步速度**由以下关系式给出:
$$ \mathrm{\mathit{N_{s}}\:=\:\frac{120\mathit{f}}{\mathit{p}}\cdot \cdot \cdot (1)} $$
其中:
**f** 是电源频率,
**P** 是电机中的极数。
同步速度以每分钟转数 (RPM) 测量。
为了获得令人满意的运行,同步电机始终保持公式 (1) 中给出的表达式。如果同步电机未能保持公式 (1) 中的上述关系,则电机将停止运行,这种情况称为电机的**失去同步**或**失步**。因此,这证明了同步电机设计为以恒定速度运行。
同步电机的运行原理
同步电机的运行原理基于**电磁相互作用定律**和**磁互锁定律**。
根据电磁相互作用定律,当导体和磁场之间存在相对运动时,导体中会感应出电动势。另一方面,当载流导体放置在磁场中时,导体上会作用一个力,该力趋于使其移动。
根据磁互锁定律,两个不同的磁场(定子的磁场和转子的磁场)相互锁定并以相同的速度旋转。这种现象称为**磁互锁**。
这两个原理解释了同步电机的运行方式。同步电机首先通过电磁相互作用启动,然后转子和定子的磁场锁定在一起,以同步速度旋转。
三相同步发电机
通过电磁感应将机械能转换为三相电能的同步电机称为**三相同步发电机**或**交流发电机**。
三相交流发电机由电枢绕组和励磁绕组组成,其中在电枢绕组中感应电动势,而励磁绕组产生工作磁场。对于三相交流发电机,电枢绕组设置在电机的定子部分,而励磁绕组设置在转子上。静止电枢绕组的主要优点是无需像直流发电机那样需要换向器。
三相同步发电机最广泛地用于发电厂发电。
三相同步电动机
将三相电能转换为机械能的同步电机称为**三相同步电动机**。
与任何其他电动机一样,同步电动机也包括两个主要部分,即定子和转子。定子带有三相电枢绕组,而转子带有励磁绕组,励磁绕组由直流电源励磁以产生一定数量的固定磁极。
同步电动机的独特之处在于它可以以恒定的速度运行,称为同步速度。然而,三相同步电动机的主要缺点是它没有自启动转矩。因此,为了启动三相同步电动机,必须通过某种辅助手段将其速度提高到接近其同步速度。
作为恒速电动机,电动机上的负载不超过极限值。如果电动机上的负载超过极限值,电动机将立即停止运行。三相同步电动机用于:以恒定速度驱动机械负载,提高系统的功率因数等。
同步电机的特点
以下是同步电机(电动机或发电机)的关键特征:
同步电动机没有自启动转矩。
同步电机是双励磁电机,因为它需要两个输入电源——一个在定子上,另一个在转子上。
同步电机以恒定速度运行,称为同步速度。
同步发电机可以产生幅度和频率恒定的电压。
同步电机可以通过改变励磁来以滞后、超前或单位功率因数运行。
与感应电动机相比,同步电动机的启动转矩相对较高。
同步电动机适用于驱动恒定和低速(通常小于 300 RPM)负载。
同步电机价格昂贵。
同步电机的构造
与任何其他旋转电机一样,同步电机(发电机或电动机)有两个基本部件:
**定子**——它是电机的静止部分,并带有电枢绕组。
**转子**——它是电机的旋转部分。同步电机的转子产生主要的磁通。
本章将讨论同步电机的定子和转子的构造方式。
定子结构
同步电机的定子包括框架、定子铁心、定子绕组和冷却机构等各个部分。框架是电机的外部部分,小型电机由铸铁制成,大型电机由焊接钢制成。框架包围整个电机组件并保护其免受机械和环境影响。
定子铁心是一个空心圆柱体,由高级硅钢片制成。硅钢片可减少电机的磁滞和涡流损耗。在定子铁心的内周缘上设有许多均匀分布的槽。三相绕组置于这些槽中。当电流流过定子绕组时,它会产生正弦磁场,从而产生电动势。
转子结构
在同步电机中,使用两种类型的转子结构,即**凸极转子**和**圆柱形转子**。
凸极转子
术语**凸极**表示**突出**。因此,凸极转子是指其磁极从转子铁心表面突出的转子,如图 2 所示。
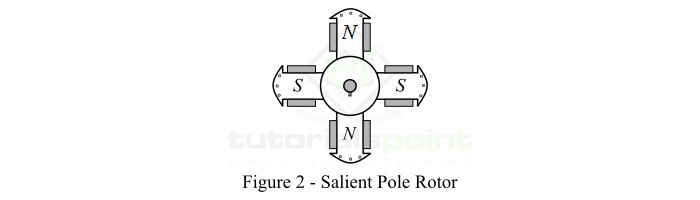
由于转子受到变化的磁场的作用,因此它由薄钢片制成以减少涡流损耗。相同尺寸的磁极通过堆叠所需长度的叠片然后铆接在一起而构成。在每个磁极铁心周围绕制励磁线圈后,将磁极安装到与转子轴键合的钢制蜘蛛上。
在每个磁极的外端,提供阻尼条以抑制负载突然变化时转子的振荡。虽然使用凸极转子的同步电机具有不均匀的空气隙,其中磁极中心下的空气隙最小,磁极之间的空气隙最大。磁极面(磁极的外端)的形状使得径向空气隙的长度从磁极中心到磁极尖端增加,因此它可以产生气隙中正弦分布的磁通。这将确保同步电机的平稳运行。
在凸极转子中,各个励磁线圈串联连接,以便它们可以产生交替的北极和南极。励磁线圈的两端通过电刷和滑环连接到直流电源。
具有凸极转子的同步电机通常具有大量的磁极,并以较低的速度运行。这些电机具有较大的直径和较短的轴向长度。
圆柱形转子
这种同步电机转子结构具有光滑的圆柱形结构。对于圆柱形转子,没有向外突出的物理极。圆柱形转子由高等级镍铬钼钢的整体锻件制成。
在转子的外圆周上,在转子的大约三分之二处均匀地切割出槽,这些槽平行于转子轴。励磁绕组放置在这些槽中。励磁绕组由直流电源供电。转子的未开槽部分形成极面。
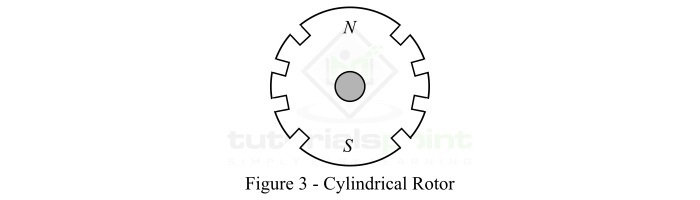
使用圆柱形转子的同步电机具有较小的直径和较长的轴向长度。圆柱形转子结构限制了离心力的影响。因此,圆柱形转子结构主要用于高速同步电机。此外,这种转子结构提供了更大的机械强度,并允许对电机进行更精确的动态平衡。
使用圆柱形转子的同步电机的主要优点是它产生的机械损耗较小。由于圆柱形转子在电机中提供了均匀的气隙,因此其运行噪音较小。
三相交流发电机的运行原理
三相交流发电机是一种同步电机,它通过电磁感应过程将机械能转换为三相电能。
正如我们在前几章中讨论的那样,三相交流发电机,也称为三相同步发电机,具有静止的电枢和旋转的磁场。在三相交流发电机中,转子绕组(充当励磁绕组)由直流电源供电,并在转子上产生交替的南北极。
三相交流发电机的运行
当转子由原动机(发动机、汽轮机等)旋转(例如逆时针方向)时,定子绕组(充当电枢绕组)被转子极的磁通切割。由于电磁感应,在电枢绕组中感应出电动势。这种感应电动势是交流电,因为转子的南北极交替地经过电枢绕组导体。我们可以用弗莱明右手定则确定感应电动势的方向。
图1显示了星形连接电枢绕组和直流励磁绕组三相交流发电机的等效电路图。(此处应插入图1)
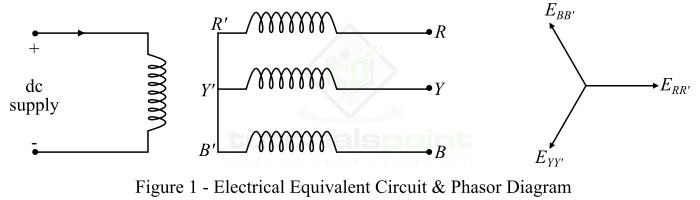
当转子旋转时,在电枢绕组中产生三相电压。产生的电压大小取决于转子旋转速度和直流励磁电流。然而,电枢每个相位的产生电压大小相同,但在空间上彼此相差120°电角度,如图所示。(此处应插入相量图)
产生电压的频率
在三相交流发电机中,产生电压的频率取决于旋转速度和电机中的磁极数。
设
N = 旋转速度,单位为RPM
P = 磁极数
则产生电压的频率由下式给出:
$$\mathrm{\mathit{f}\:=\:\frac{\mathit{NP}}{120}\:\mathrm{Hz}\:\cdot \cdot \cdot (1)}$$
需要注意的是,N是同步速度,因为交流发电机是一种同步电机,其转子始终以同步速度旋转。
三相交流发电机的电动势方程
给出三相交流发电机电枢绕组中感应电动势值的数学关系称为其电动势方程。
设
N = 旋转速度,单位为RPM
P = 转子上的磁极数
$\phi$ = 每极磁通,单位为韦伯
Z = 每相电枢导体数
则,在一转中,每个定子导体被$\mathit{P\phi }$ 韦伯的磁通切割,即:
$$\mathrm{\mathit{d\phi }\:=\:\mathit{P\phi }}$$
完成一转所需的时间为:
$$\mathrm{\mathit{dt }\:=\:\frac{60}{\mathit{N}}}$$
因此,每个电枢导体中感应的平均电动势为:
$$\mathrm{\mathrm{每导体电动势}\:=\:\mathit{\frac{d\phi }{dt}}\:=\:\frac{\mathit{P\phi }}{(60/\mathit{N})}\:=\:\frac{\mathit{P\phi N}}{\mathrm{60}}}$$
由于Z是每相电枢绕组中的总导体数,则
$$\mathrm{\mathrm{每相平均电动势, }\mathit{E_{av}/\mathrm{相}}\:=\:\mathit{Z\times }\frac{\mathit{P\phi N}}{\mathrm{60}}}$$
$$\mathrm{\because \mathit{N}\:=\:\frac{120\mathit{f}}{\mathit{P}}}$$
则,
$$\mathrm{\mathit{E_{av}/}\mathrm{相}\:=\:\frac{\mathit{P\phi Z}}{60}\times \frac{120\mathit{f}}{\mathit{P}}\:=\:2\mathit{f\phi Z}\:\mathrm{伏特}}$$
现在,每相产生的电动势的有效值为:
$$\mathrm{\mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:\left ( \mathit{E_{av}/\mathrm{相}} \right )\times \mathrm{形状系数}}$$
在实践中,我们认为三相交流发电机产生正弦电压,其形状系数为1.11。
$$\mathrm{\mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:2\mathit{f\phi Z}\times 1.11}$$
$$\mathrm{\therefore \mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:2.22\mathit{f\phi Z}\:\mathrm{伏特}\:\cdot \cdot \cdot (2)}$$
有时,指定每相的匝数 (T) 而不是每相的导体数。在这种情况下,我们有:
$$\mathrm{\mathit{Z}\:=\:2\mathit{T}}$$
$$\mathrm{\therefore \mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:\mathit{E_{ph}}\:=\:4.44\mathit{f\phi T}\:\mathrm{伏特}\:\cdot \cdot \cdot (3)}$$
公式(2)和(3)中的表达式称为三相交流发电机的电动势方程。
数值例子(1)
具有6个磁极并以1200 RPM旋转的三相交流发电机产生的电压频率是多少?
解答
已知数据:
P = 6;
N = 1200 RPM
$$\mathrm{\mathrm{频率,}\mathit{f}\:=\:\frac{\mathit{NP}}{120}\:=\:\frac{1200\times 6}{120}}$$
$$\mathrm{\therefore\mathit{f} \:=\:60\:Hz}$$
数值例子(2)
一个4极、3相、50 Hz交流发电机的电枢有24个槽,每个槽有10个导体。一个磁极有0.03 Wb的磁通进入电枢。计算每相感应电动势。
解答
$$\mathrm{\mathrm{总导体数}\:=\:24\times 10\:=\:240}$$
$$\mathrm{\mathrm{每相导体数,}\mathit{Z}\:=\:\frac{240}{3}\:=\:80}$$
$$\mathrm{\therefore \mathit{E_{ph}}\:=\:2.22\mathit{f\phi Z}\:=\:2.22\times 50\times 0.03\times 80}$$
$$\mathrm{\mathit{E_{ph}}\:=\:266.4\:V}$$
同步电机中的电枢反应
交流发电机的电枢反应
当三相交流发电机空载运行时,其电枢绕组中将没有电流流过。因此,气隙中产生的磁通仅由转子磁极产生。但是,当交流发电机负载运行时,流过电枢绕组的三相电流将在气隙中产生旋转磁场。结果,气隙中的合成磁通发生变化。这种效应称为电枢反应,可以定义如下:
流过三相交流发电机电枢绕组的电流,产生的磁动势(MMF)产生磁通。这种电枢磁通与主极磁通相互作用,导致气隙中的合成磁通量小于或大于原来的主极磁通量。电枢磁通对主极磁通的影响称为电枢反应。
在三相交流发电机中,电枢反应的影响取决于电枢电流的大小和负载的功率因数。这意味着负载的功率因数决定电枢反应磁通是否会扭曲、抵消或辅助主磁通。
以下讨论解释了同步电机在不同功率因数下的电枢反应性质:
功率因数为1 - 当交流发电机以功率因数为1的负载供电时,即纯电阻负载,电枢反应的作用是扭曲主磁通。这称为电枢反应的横向磁化效应。
滞后功率因数 - 当交流发电机以滞后功率因数的负载供电时,即纯感性负载,电枢反应的作用是部分去磁和部分横向磁化。这会导致产生电压降低。
超前功率因数 - 当交流发电机以超前功率因数的负载供电时,即纯容性负载,电枢反应的作用是部分磁化和部分横向磁化。这会导致产生电压升高。
同步电动机的电枢反应
当同步电机以电动机模式运行时,电枢反应磁通处于反相,这意味着电枢反应的性质与交流发电机的相反。
以下几点解释了同步电机在电动机模式下运行时电枢反应的影响:
滞后功率因数 - 当同步电动机以滞后功率因数吸取电流时,电枢反应的作用是部分磁化和部分横向磁化。
超前功率因数 - 当同步电动机以超前功率因数吸取电流时,电枢反应的作用是部分去磁和部分横向磁化。
三相交流发电机的输出功率
考虑一个具有圆柱形转子的三相交流发电机,它以滞后功率因数运行。
设:
E = 每相感应电动势
V = 每相端电压
Ia = 每相电枢电流
cos$\phi$ = 负载的功率因数(滞后)
$\delta$ = 功率角(E和V之间的角度)
因此,三相交流发电机的输出功率由下式给出:
$$\mathrm{\mathit{P_{0}}\:=\:3\mathit{VI_{a}cos\phi }\cdot \cdot \cdot (1)}$$
三相交流发电机的近似输出功率
在三相交流发电机中,电枢电路的电阻$R_{a}$与电机的同步电抗$X_{s}$相比非常小。因此,我们可以忽略电枢电阻($R_{a}$),然后得到交流发电机的近似等效电路,如图1所示。(此处应插入图1) 电路的相量图也如图1所示。(此处应插入图1)
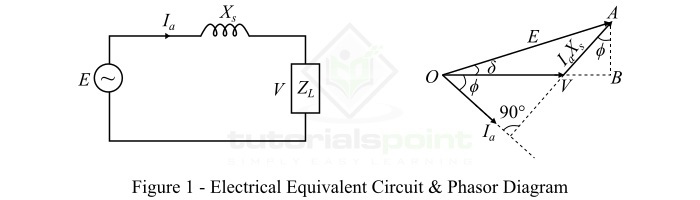
从相量图中,我们得到:
$$\mathrm{\mathit{AB}\:=\:\mathit{I_{a}X_{s}cos\phi }\:=\:\mathit{E}\:\mathrm{sin\delta }}$$
$$\mathrm{\Rightarrow \mathit{I_{a}cos\phi }\:=\:\frac{\mathit{E\:\mathrm{sin\delta }}}{\mathit{X_{s}}}\cdot \cdot \cdot (2)}$$
现在,从公式(1)和(2),我们得到:
$$\mathrm{\mathit{P_{0}}\:=\:\frac{3\mathit{EV\:\mathrm{sin\delta }}}{\mathit{X_{s}}}\cdot \cdot \cdot (3)}$$
公式3中的表达式给出了三相交流发电机的近似输出功率。
当交流发电机以恒定速度和恒定的励磁电流运行时,Xs和E都是恒定的,因此端电压V也是恒定的。因此,从公式3可以看出:
$$\mathrm{\mathit{P_{0}}\propto \:\mathrm{sin\delta }}$$
我们知道,当$\delta$ = 90°时,则
$$\mathrm{\mathrm{sin\:90^{\circ}}\:=\:1}$$
因此,交流发电机在$$ =90°时提供最大功率,由下式给出:
$$\mathrm{\mathit{P_{max}}\:=\:\frac{3\mathit{EV}}{\mathit{X_{s}}}}\cdot \cdot \cdot (4)$$
公式4给出的最大功率称为交流发电机的静态稳定极限。
数值例子
一台三相、11 kV、3 MVA星形连接交流发电机每相同步电抗为10 $\Omega$。其励磁使得产生的线电压为15 kV。当交流发电机连接到无限大母线时。忽略电枢电阻,计算该励磁下交流发电机的最大输出功率。
解答
已知数据:
$$\mathrm{\mathrm{线电压,}\mathit{V_{L}}\:=\:11\:kV\:=\:11000\:V}$$
$$\mathrm{\therefore\:\mathrm{每相端电压,}\mathit{V}\:=\:\frac{11000}{\sqrt{3}}\:=\:6350.85\:V}$$
$$\mathrm{\mathrm{产生的线电压}\:=\:15\:kV\:=\:15000\:V}$$
$$\mathrm{\therefore\:\mathrm{每相产生的电动势,}\mathit{E}\:=\:\frac{15000}{\sqrt{3}}\:=\:8660.25\:V}$$
$$\mathrm{\mathrm{每相同步电抗,}\:\mathit{X_{s}}\:=\:10\:\Omega }$$
因此,交流发电机的最大输出功率将为:
$$\mathrm{\mathit{P_{max}}\:=\:\frac{3\mathit{EV}}{\mathit{X_{s}}}\:=\:\frac{3\times 8660.25\times 6350.85}{10}}$$
$$\mathrm{\therefore \mathit{P_{max}}\:=\:16499\times 10^{3}W\:=\:16499\:\mathrm{kW}}$$
三相交流发电机的损耗和效率
三相交流发电机的损耗
三相交流发电机中发生的损耗可以分为以下四类:
铜损
铁损或铁芯损耗
机械损耗
杂散负载损耗
通读本节,了解三相交流发电机中发生的各种损耗类型。
铜损
铜损发生在交流发电机的电枢绕组和转子绕组中,这是由于当电流流过它们时,它们的电阻造成的。因此,这些损耗也称为I2R损耗。
铁损或铁芯损耗
铁损或铁芯损耗发生在交流发电机的铁部件(如定子铁芯和转子铁芯)中。这些损耗包括磁滞损耗和涡流损耗。铁芯损耗的产生是因为交流发电机的各种铁部件都受到变化的磁场的影响。
机械损耗
交流发电机的机械损耗发生在转动部件中,例如转子、轴、轴承等。机械损耗主要分为两种:摩擦损耗和风损。摩擦损耗是由于发电机轴承的摩擦造成的,而风损是由于发电机的旋转部件与发电机外壳内的空气之间的摩擦造成的。
附加负载损耗
此类损耗难以精确计算,也称为杂散损耗。附加负载损耗可能由以下原因引起:
电枢反应导致主磁通畸变。
电枢导体横截面上的电流分布不均匀。
在实际计算中,我们将附加负载损耗取为满载损耗的1%。
注意
铁损和机械损耗合称为旋转损耗,因为这些损耗是由于转子旋转而产生的。
发电机中发生的这些损耗都会转化为热量,导致温度升高和效率降低。
三相交流发电机效率
发电机的输出功率与输入功率之比称为发电机效率。效率通常以百分比表示。
$\mathrm{\mathrm{效率,} \: \eta \:=\:\frac{输出功率}{输入功率}\times 100\%\:=\:\frac{输出功率}{输出功率+损耗}\times 100\%}$
现在,我们将推导三相交流发电机效率的表达式。为此,考虑一个在滞后功率因数下运行的三相交流发电机。
设:
V= 每相端电压
Ia = 每相电枢电流
cos $\phi$ = 负载功率因数(滞后)
因此,三相交流发电机的输出功率由下式给出:
$$\mathrm{\mathit{P_{0}}\:=\:3\:\mathit{VI_{a}cos\:\phi }}$$
发电机的损耗为:
$$\mathrm{\mathrm{电枢铜损,}\mathit{P_{cu}}\:=\:3\:\mathit{I_{\mathit{a}}^{\mathrm{2}}R_{a}}}$$
$$\mathrm{\mathrm{励磁绕组铜损}\:=\:\mathit{V_{f}I_{f}}}$$
其中,Vf是励磁绕组上的直流电压,If是直流励磁电流。
$$\mathrm{\mathrm{旋转损耗,}\mathit{P_{r}}\:=\:\mathrm{铁损\:+\:机械损耗}}$$
$$\mathrm{\mathrm{附加负载损耗}\mathit{P_{s}}}$$
$$\mathrm{\therefore \mathrm{发电机总损耗,}\mathit{P_{loss}}\:=\:3\:\mathit{I_{a}^{2}R_{a}\:+\:P_{r}\:+\:P_{s}\:+\:V_{f}I_{f}}}$$
由于转子旋转速度恒定,因此旋转损耗恒定。励磁绕组铜损也恒定。如果我们假设附加负载损耗为恒定值,则有:
$$\mathrm{\mathrm{总恒定损耗,}\mathit{P_{c}}\:=\:\mathit{P_{r}\:+\:P_{s}\:+\:V_{f}I_{f}}}$$
$$\mathrm{\therefore\:\mathrm{可变损耗} \:=\:\mathrm{3}\mathit{I_{a}^{\mathrm{2}}R_{a}}}$$
因此,发电机效率由下式给出:
$$\mathrm{\eta \:=\:\frac{\mathit{P_{0}}}{\mathit{P_{0}+\mathrm{损耗}}}\:=\:\frac{3\mathit{VI_{a}cos\phi }}{3\mathit{VI_{a}cos\phi \:+\:\mathrm{3}\mathit{I_{a}^{\mathrm{2}}R_{a}}\:+P_{c}}}\cdot \cdot \cdot (1)}$$
公式(1)可用于确定三相交流发电机的效率。
最大效率的条件
当可变损耗等于恒定损耗时,发电机效率最高,即:
$$\mathrm{\mathit{P_{c}}\:=\:3\:\mathit{I_{a}^{\mathrm{2}}R_{a}}\cdot \cdot \cdot (2)}$$
实际上,交流发电机的最大效率通常出现在额定满载的85%左右。
数值例子
一台三相交流发电机每相端电压为230 V,每相电枢电流为14.4 A。发电机电枢电路电阻为0.5Ω,恒定损耗为200瓦。如果它以0.8滞后功率因数供电,计算发电机的效率和最大效率。
解答
$$\mathrm{\mathrm{效率,}\eta \:=\:\frac{3\mathit{VI_{a}cos\phi }}{3\mathit{VI_{a}cos\phi \:+\:\mathrm{3}\mathit{I_{a}^{\mathrm{2}}R_{a}}\:+P_{c}}}}$$
$$\mathrm{\Rightarrow\:\eta \:=\:\frac{3\times 230\times 14.4\times 0.8}{\left ( 3\times 230\times 14.4\times 0.8 \right )\:+\:\left ( 3\times 14.4^{2}\times 0.5 \right )\:+\:200}}$$
$$\mathrm{\therefore \eta \:=\:0.9395\:=\:93.95\%}$$
对于发电机的最大效率,
$$\mathrm{\mathit{P_{c}}\:=\:3\:\mathit{I_{a}^{\mathrm{2}}R_{a}}}$$
$$\mathrm{\therefore \eta_{max} \:=\:\frac{3\mathit{VI_{a}cos\phi }}{3\mathit{VI_{a}cos\phi \:+\:\mathrm{2}\mathit{P_{c}}}}\:=\:\frac{3\times 230\times 14.4\times 0.8}{\left ( 3\times 230\times 14.4\times 0.8 \right )\:+\:\left (2\times 200 \right )}}$$
$$\mathrm{\therefore \eta_{max} \:=\:0.9521\:=\:95.21\%}$$
三相同步电机的运行原理
将三相电能转换为机械能的三相同步电机称为三相同步电动机。
三相同步电动机是恒速电机,它以同步速度运行。三相同步电动机的同步速度由下式给出:
$$ \mathrm{\mathit{N_{s}}\:=\:\frac{120\mathit{f}}{\mathit{p}}\cdot \cdot \cdot (1)} $$
其中,f是电源频率,P是电机中的磁极对数。
与任何其他电动机一样,三相同步电动机也由两个主要部分组成,即定子和转子。定子装有三相电枢绕组,并从三相交流电源接收电力。转子是旋转部件,带有励磁绕组,励磁绕组由外部直流电源激励。
同步电动机的最主要缺点是它不能自启动,因此必须使用辅助手段启动它。
三相同步电机的运行原理
考虑一个具有凸极式转子的三相同步电动机,该转子有两个磁极,分别为$\mathit{N_{\mathrm{2}}}$和$\mathit{S_{\mathrm{2}}}$。因此,定子也将绕制成两个磁极,分别为$\mathit{N_{\mathrm{1}}}$和$\mathit{S_{\mathrm{1}}}$。直流电压施加到转子绕组,平衡的三相交流电压施加到定子绕组。
定子绕组产生一个旋转磁场,该磁场以同步速度($\mathit{N_{\mathit{s}}}$)围绕定子旋转。流过转子绕组的直流电流在转子中产生两个磁极,只要转子不转动,这两个磁极产生的磁场就是静止的。因此,在这种情况下,我们有一对旋转的电枢磁极 ($\left ( \mathit{N_{\mathrm{1}}}-\mathit{S_{\mathrm{1}}} \right )$)和一对静止的转子磁极 ($\left ( \mathit{N_{\mathrm{2}}}-\mathit{S_{\mathrm{2}}} \right )$)。
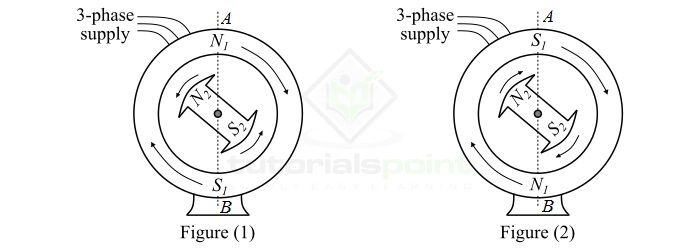
现在,考虑定子磁极位于A和B位置的瞬间,如图1所示。很明显,磁极$\mathit{N_{\mathrm{1}}}$和$\mathit{N_{\mathrm{2}}}$互相排斥,磁极$\mathit{S_{\mathrm{1}}}$和$\mathit{S_{\mathrm{1}}}$也是如此。因此,转子倾向于逆时针旋转。在交流电源半个周期后,定子磁极的极性反转,但转子磁极的极性保持不变,如图2所示。在这种情况下,磁极$\mathit{S_{\mathrm{1}}}$和$\mathit{N_{\mathrm{2}}}$互相吸引,磁极$\mathit{N_{\mathrm{1}}}$和$\mathit{S_{\mathrm{2}}}$也是如此。因此,转子现在倾向于顺时针旋转。
由于定子磁极迅速改变极性,它们倾向于先在一个方向上拉动转子,然后在交流电半个周期后在另一个方向上拉动转子。由于转子上的双向转矩和转子的高惯性,同步电动机无法启动。因此,同步电动机没有自启动转矩。
使同步电动机自启动
同步电动机不能自行启动。为了使电动机能够自启动,在转子上设置了一个鼠笼式绕组,称为阻尼绕组。阻尼绕组由嵌入转子凸极极靴槽中的铜条组成,如图3所示。
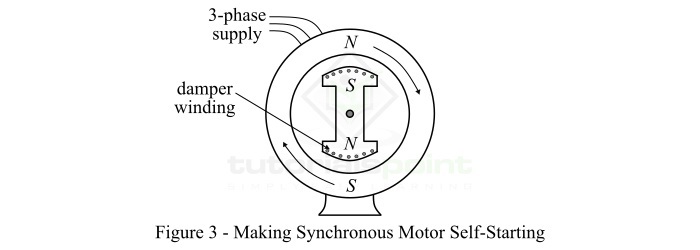
这些阻尼绕组用于使同步电动机自行启动,解释如下:
最初,三相电源供电给定子绕组,而转子绕组保持断开状态。定子绕组的旋转磁场在阻尼绕组中感应出电流,由于电磁力,转子开始运动。因此,同步电动机作为异步电动机启动。
一旦电动机达到接近同步速度的速度,转子绕组就会从直流电源励磁。现在,转子上的磁极面对极性相反的定子磁极,并在它们之间建立强大的磁吸引力。因此,转子磁极与定子的旋转磁极锁定。因此,转子以与定子磁极相同的速度旋转,即同步速度。
由于转子现在以与定子磁场相同的速度旋转,阻尼条不切割任何磁通,因此在其中没有感应电流。因此,转子的阻尼绕组实际上从电动机的运行中移除。
通过这种方式,同步电动机可以自启动。必须注意的是,由于定子和转子磁极之间的磁互锁,同步电动机只能以同步速度运行。
同步电机的等效电路和功率因数
同步电动机的等效电路
同步电动机是一个双激系统,这意味着它连接到两个电力系统,其中三相交流电源连接到电枢绕组,直流电源连接到转子绕组。图1显示了三相同步电动机的每相等效电路。

这里,V是施加到电机的每相电压,Ra是每相电枢电阻,$X_{s}$是每相同步电抗。这两个参数(即$R_{a}$和$X_{s}$)给出电机的每相同步阻抗($Z_{s}$)。
从同步电动机的等效电路(如图1所示)中,我们可以写出它的电压方程为:
$$\mathrm{\mathit{V}\:=\:\mathit{E_{b}+I_{a}Z_{s}}}$$
$$\mathrm{\Rightarrow \mathit{V}\:=\:\mathit{E_{b}+I_{a}\left ( R_{a} +jX_{s}\right )}}$$
其中,粗体字母表示相量。
因此,每相电枢电流由下式给出
$$\mathrm{I_{a}\:=\:\frac{\mathit{V-E_{b}}}{\mathit{Z_{s}}}\:=\:\frac{\mathit{V-E_{b}}}{\left ( \mathit{R_{a}+jX_{s}}\right )}\:=\:\frac{\mathit{E_{r}}}{\mathit{R_{a}+jX_{s}}}}$$
其中,$\mathit{E_{r}}$是电枢电路中的合成电压。
同步电动机的电枢电流和同步阻抗是具有幅值和相角的相量。因此,电枢电流的幅值由下式给出:
$$\mathrm{\left|I_{a} \right|\:=\:\frac{\mathit{V-E_{b}}}{\mathit{Z_{s}}}\:=\:\frac{\mathit{E_{r}}}{\mathit{Z_{s}}}}$$
同步阻抗的幅值由下式给出:
$$\mathrm{\left|Z_{s} \right|\:=\:\sqrt{\mathit{R_{a}^{\mathrm{2}}+X_{s}^{\mathrm{2}}}}}$$
等效电路和上述方程有助于理解同步电动机的运行,如:
当励磁电流使得$\mathit{E_{b}=V}$时,则称同步电动机为正常励磁。
当励磁电流使得$\mathit{E_{b}<V}$时,则称同步电动机为欠励磁。
当励磁电流使得$\mathit{E_{b}> V}$时,则称同步电动机为过励磁。
正如我们将在下一节中看到的,同步电动机的励磁会影响其功率因数。
同步电动机的功率因数
同步电动机的最重要的特性之一是,可以通过改变励磁来使其在超前、滞后或单位功率因数下运行。以下讨论解释了励磁变化如何影响同步电动机的功率因数:
当转子励磁电流足以产生所有所需的磁通量时,则机器不需要额外的无功功率。因此,电动机将在单位功率因数下运行。
当转子励磁电流小于所需电流时,即电动机欠励磁。在这种情况下,电动机将从电源吸收无功功率以提供剩余的磁通量。因此,电动机将在滞后功率因数下运行。
当转子励磁电流超过所需电流时,即电机过励磁。在这种情况下,电机将向三相线路提供无功功率,并表现为无功功率源。因此,电机将在**超前功率因数**下运行。
因此,我们可以得出结论:**同步电机欠励磁时吸收无功功率,过励磁时发出无功功率。**
同步电机产生的功率
本章将推导三相同步电机**输出机械功率**(Pm)的表达式。这里,我们将忽略同步电机的电枢电阻Ra。则电枢铜损将为零,因此电机输出的机械功率等于电机的输入功率(Pin),即:
$$\mathrm{\mathit{P_{m}}\:=\:\mathit{P_{in}}}$$
现在,考虑一个欠励磁(即,Eb<V)的三相同步电机,其电枢电阻为零(即,Ra = 0),并且正在驱动机械负载。
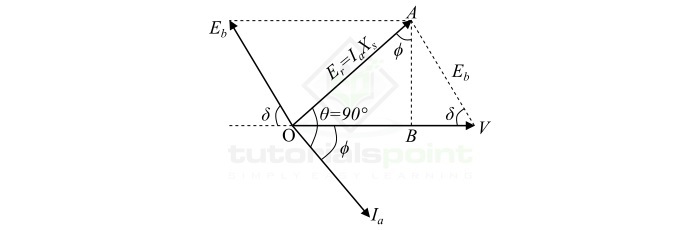
该同步电机一相的相量图如图所示。由于电机欠励磁,因此它将在滞后功率因数下运行,例如(cos $\phi$)。从相量图可以看出,$\mathit{E_{r}}\:=\:I_{a}X_{s}$,并且每相电枢电流$I_{a}$滞后于合成电动势$\mathit{E_{r}}$ 90°。
因此,电机的每相输入功率由下式给出:
$$\mathrm{\mathit{P_{in}}\:=\mathit{VI_{a}}\:cos\:\phi \:\cdot \cdot \cdot (1)}$$
由于$\mathit{P_{m}}$等于$\mathit{P_{in}}$,因此:
$$\mathrm{\mathit{P_{m}}\:=\mathit{VI_{a}}\:cos\:\phi \:\cdot \cdot \cdot (2)}$$
从相量图中,我们有:
$$\mathrm{\mathit{AB}\:=\mathit{I_{a}X_{s}}\:cos\:\phi \:=\:\mathit{E}_{\mathit{b}}\:sin\:\delta}$$
$$\mathrm{\therefore \mathit{I_{a}\:cos\phi \:=\:\frac{E_{b}\:sin\delta }{\mathit{X_{s}}}}\:\cdot \cdot \cdot (3)}$$
利用公式(2)和(3),我们得到:
$$\mathit{P_{m}\:=\:\frac{\mathit{VE_{b}}sin\delta }{X_{s}}}\cdot \cdot \cdot (4)$$
这是同步电机每相输出机械功率(Pm)的表达式。
对于电机的三相,输出的机械功率由下式给出:
$$\mathit{P_{m}\:=\:\frac{3\mathit{VE_{b}}sin\delta }{X_{s}}}\cdot \cdot \cdot (5)$$
此外,从公式(4)和(5)可以看出,当功率角($\delta$= 90°)(电角度)时,输出的机械功率最大。因此:
每相:
$$\mathit{P_{max}\:=\:\frac{\mathit{VE_{b}}}{X_{s}}}\cdot \cdot \cdot (6)$$
三相:
$$\mathit{P_{max}\:=\:\frac{\mathit{3VE_{b}}}{X_{s}}}\cdot \cdot \cdot (7)$$
要点
关于三相同步电机输出的机械功率,需要注意以下几点:
同步电机输出的机械功率随着功率角($\delta$)的增加而增加,反之亦然。
如果功率角($\delta$)为零,则同步电机无法产生机械功率。
当同步电机的励磁被减小到零时,即($E_{b}$ = 0),电机输出的机械功率也为零,即电机将停止运行。
数值例子
一台三相4000 kW,3.3 kV,200 RPM,50 Hz的同步电机,每相同步电抗为1.5 $\Omega$。满载时,功率角为22°(电角度)。如果每相产生的反电动势为1.7 kV,计算输出的机械功率。最大机械功率是多少?
解答
已知数据:
每相电压,$\mathit{V}\:=\:\frac{3.3}{\sqrt{3}}\:=\:1.9\:kV$
每相反电动势,$\mathit{E_{b}}\:=\:1.7\:kV$
同步电抗,$X_{s}\:=\:1.5\Omega $
功率角,$\delta \:=\:22^{^{\circ}}$
因此,电机输出的机械功率为:
$$\mathrm{\mathit{P_{m}}\:=\:\frac{3\:\mathit{VE_{b}\:sin\delta} }{\mathit{X_{s}}}\:=\:\frac{3\times 1.9\times 1.7\times \mathrm{sin}\:22^{\circ}}{1.5}}$$
$$\mathit{\therefore P_{m}}\:=\:2.42\times 10^{6}\:W\:=\:2.42\:MW$$
当($\delta$ =90°)时,输出的机械功率最大:
$$\mathit{P_{max}}\:=\:\frac{3\mathit{VE_{b}}}{X_{s}}\:=\:\frac{3\times 1.9\times 1.7}{1.5}$$
$$\mathit{\therefore P_{max}}\:=\:6.46\:\mathrm{MW}$$