感应电动势的概念

根据**电磁感应原理**，当与导体或线圈相连的磁通量发生变化时，导体或线圈中就会感应出电动势。在实践中，可以使用以下两种方法来实现磁通量链路的改变。

方法 1 - 导体在静止磁场中运动

我们可以使导体或线圈在静止磁场中以某种方式运动，使得与导体或线圈相连的磁通量的大小发生变化。因此，在导体中会感应出电动势。这种感应电动势称为**动生电动势**。之所以这样称呼，是因为电动势是在运动的导体中感应产生的。动生电动势的例子是交流发电机和直流发电机中产生的电动势。

当静止的导体或线圈置于运动或变化的磁场中时，导体或线圈中会感应出电动势。以这种方式感应出的电动势称为**静生电动势**。之所以这样称呼，是因为电动势是在静止的导体中感应产生的。变压器中感应出的电动势就是静生电动势的一个例子。

因此，从上述讨论可以清楚地看出，感应电动势可以分为两种主要类型，即：

如上节所述，**动生电动势**是在置于静止磁场中的运动导体或线圈中感应产生的。动生电动势的表达式可以推导如下：

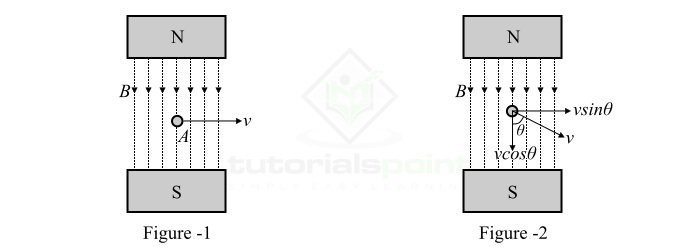
考虑一根长度为l米的单根导体，位于磁通密度为B Wb/m²的均匀磁场中，如图 1 所示。该导体相对于磁场以v m/s的速度垂直运动。

现在，如果导体在dt秒内移动一小段距离dx，则导体扫过的面积为：

$$\mathrm{\mathit{A\:=\:l\times dx\:}\mathrm{m^{\mathrm{2}}}}$$

因此，导体切割的磁通量为：

$$\mathrm{\mathit{d\phi }\:=\:\mathrm{磁通密度\times 扫过的面积}}$$

$$\mathrm{\Rightarrow \mathit{d\phi }\:=\:\mathit{B\times l\times dx}\:\mathrm{Wb}}$$

根据法拉第电磁感应定律，导体中感应的电动势为：

$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\:=\:\mathit{N}\frac{\mathit{Bldx}}{\mathit{dt}}}$$

由于我们只考虑了一根导体，因此N = 1。

$$\mathrm{\mathit{e}\:=\:\mathit{Blv}\:\mathrm{伏特}\cdot \cdot \cdot (1)}$$

其中，v = dx/dt，为导体在磁场中的速度。

如果导体在磁场中存在角运动，并且导体相对于磁场以角度 θ 运动，如图 2 所示。则导体穿过磁场的速度等于“vsinθ”。因此，感应电动势为：

$$\mathrm{\mathit{e}\:=\:\mathit{B\:l\:v}\:\mathrm{sin\mathit{\theta }}\:\mathrm{伏特}\cdot \cdot \cdot (2)}$$

当静止导体置于变化的磁场中时，导体中感应的电动势称为**静生电动势**。静生电动势进一步分为以下两种类型：

当由于自身磁通量链路的改变而在导体或线圈中感应出电动势时，称为**自感电动势**。

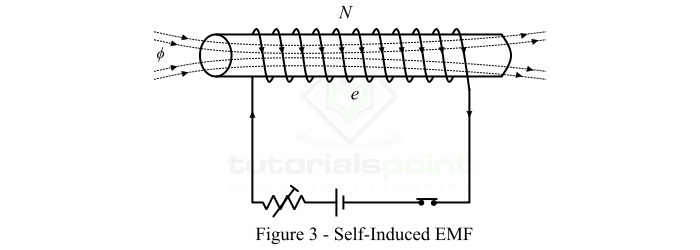
考虑一个N匝线圈，如图 3 所示。流过线圈的电流在线圈中建立磁场。如果线圈中的电流发生变化，则与线圈相连的磁通量也会发生变化。根据法拉第电磁感应定律，这个变化的磁场在线圈中感应出电动势。这种电动势称为自感电动势，自感电动势的大小由下式给出：

$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}}$$

由于邻近线圈变化的磁场在线圈中感应出的电动势称为**互感电动势**。

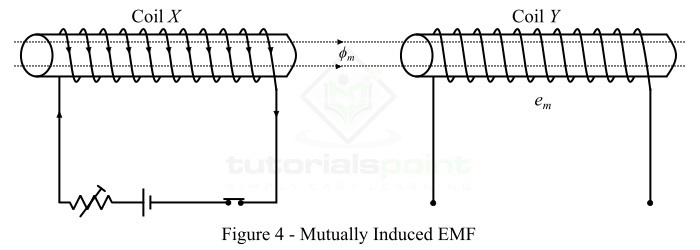
考虑两个线圈X和Y彼此相邻放置，如图 4 所示。这里，线圈X产生的磁通量的一部分与线圈 Y 相连。线圈 X 的磁通量，它同时与线圈X和Y相连，称为**互感磁通量($\mathit{\phi _{m}}$)**。

如果线圈X中的电流发生变化，则互感磁通量也会发生变化，从而在线圈中感应出电动势。其中，在线圈X中感应出的电动势称为自感电动势，在线圈Y中感应出的电动势称为**互感电动势**。

根据法拉第定律，互感电动势的大小由下式给出：

$$\mathrm{\mathit{e_{m}}\:=\:\mathit{N_{Y}}\frac{\mathit{d\phi _{m}}}{\mathit{dt}}}$$

其中，$\mathit{N_{Y}}$是线圈 Y 的匝数，$\frac{\mathit{d\phi _{m}}}{\mathit{dt}}$是互感磁通量的变化率。

打印页面