三相交流发电机的工作原理

---

---

三相交流发电机是一种同步电机，它通过电磁感应过程将机械能转换为三相电能。

正如我们在前面的章节中讨论的那样，三相交流发电机，也称为三相同步发电机，具有静止的定子和旋转的磁场。在三相交流发电机中，转子绕组（用作励磁绕组）由直流电源供电，并在转子上产生交替的南北极。

三相交流发电机的运行

当转子由原动机（发动机、涡轮机等）旋转（例如逆时针方向）时，定子绕组（用作电枢绕组）被转子磁极的磁通切割。由于电磁感应，在电枢绕组中产生电动势。由于转子的南北极交替通过电枢绕组导体，因此产生的电动势是交变的。我们可以用弗莱明右手定则确定感应电动势的方向。

星形连接电枢绕组和直流励磁绕组三相交流发电机的等效电路如图1所示。

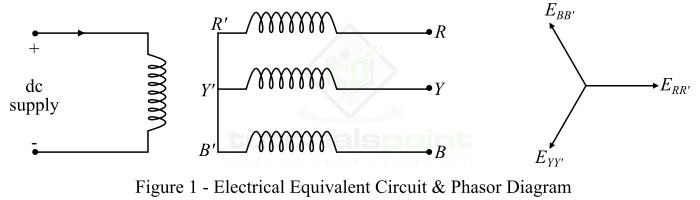
当转子旋转时，在电枢绕组中产生三相电压。产生的电压幅值取决于转子旋转速度和直流励磁电流。但是，电枢每个相位的电压幅值相同，但在空间上彼此相差120°电角度，如相量图所示。

产生电压的频率

在三相交流发电机中，产生电压的频率取决于旋转速度和电机中的磁极数。

设

• N = 旋转速度，单位为RPM

• P = 磁极数

则产生电压的频率由下式给出：

$$\mathrm{\mathit{f}\:=\:\frac{\mathit{NP}}{120}\:\mathrm{Hz}\:\cdot \cdot \cdot (1)}$$

需要注意的是，N是同步速度，因为交流发电机是一种同步电机，其转子始终以同步速度旋转。

三相交流发电机的电动势方程式

给出三相交流发电机电枢绕组中感应电动势值的数学关系称为其电动势方程式。

设

• N = 旋转速度，单位为RPM

• P = 转子上的磁极数

• $\phi$ = 每极磁通，单位为韦伯

• Z = 每相电枢导体数

则在一个旋转周期内，每个定子导体被$\mathit{P\phi }$韦伯的磁通切割，即：

$$\mathrm{\mathit{d\phi }\:=\:\mathit{P\phi }}$$

此外，完成一个旋转周期所需的时间为：

$$\mathrm{\mathit{dt }\:=\:\frac{60}{\mathit{N}}}$$

因此，每个电枢导体中感应的平均电动势为：

$$\mathrm{\mathrm{每个导体的电动势}\:=\:\mathit{\frac{d\phi }{dt}}\:=\:\frac{\mathit{P\phi }}{(60/\mathit{N})}\:=\:\frac{\mathit{P\phi N}}{\mathrm{60}}}$$

由于Z是每相电枢绕组中导体的总数，则

$$\mathrm{\mathrm{每相平均电动势, }\mathit{E_{av}/\mathrm{相}}\:=\:\mathit{Z\times }\frac{\mathit{P\phi N}}{\mathrm{60}}}$$

$$\mathrm{\because \mathit{N}\:=\:\frac{120\mathit{f}}{\mathit{P}}}$$

然后，

$$\mathrm{\mathit{E_{av}/}\mathrm{相}\:=\:\frac{\mathit{P\phi Z}}{60}\times \frac{120\mathit{f}}{\mathit{P}}\:=\:2\mathit{f\phi Z}\:\mathrm{伏特}}$$

现在，每相产生的电动势的有效值为：

$$\mathrm{\mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:\left ( \mathit{E_{av}/\mathrm{相}} \right )\times \mathrm{形状因数}}$$

在实践中，我们认为三相交流发电机产生正弦电压，其形状因数为1.11。

$$\mathrm{\mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:2\mathit{f\phi Z}\times 1.11}$$

$$\mathrm{\therefore \mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:2.22\mathit{f\phi Z}\:\mathrm{伏特}\:\cdot \cdot \cdot (2)}$$

有时，会指定每相匝数（T）而不是每相导体数。在这种情况下，我们有：

$$\mathrm{\mathit{Z}\:=\:2\mathit{T}}$$

$$\mathrm{\therefore \mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:\mathit{E_{ph}}\:=\:4.44\mathit{f\phi Z}\:\mathrm{伏特}\:\cdot \cdot \cdot (3)}$$

公式（2）和（3）中的表达式称为三相交流发电机的电动势方程式。

数值示例（1）

一个具有6个磁极并以1200 RPM旋转的三相交流发电机产生的电压频率是多少？

解答

已知数据：

• P = 6;

• N = 1200 RPM

$$\mathrm{\mathrm{频率,}\mathit{f}\:=\:\frac{\mathit{NP}}{120}\:=\:\frac{1200\times 6}{120}}$$

$$\mathrm{\therefore\mathit{f} \:=\:60\:Hz}$$

数值示例（2）

一个4极、3相、50 Hz的交流发电机的电枢有24个槽，每个槽有10个导体。一个磁极进入电枢的磁通为0.03 Wb。计算每相感应电动势。

解答

$$\mathrm{\mathrm{导体总数}\:=\:24\times 10\:=\:240}$$

$$\mathrm{\mathrm{每相导体数,}\mathit{Z}\:=\:\frac{240}{3}\:=\:80}$$

$$\mathrm{\therefore \mathit{E_{ph}}\:=\:2.22\mathit{f\phi Z}\:=\:2.22\times 50\times 0.03\times 80}$$

$$\mathrm{\mathit{E_{ph}}\:=\:266.4\:V}$$