理想变压器与实际变压器

---

---

理想变压器

理想变压器是一个想象中的变压器模型，它具有以下特征：

• 初级和次级绕组的电阻可以忽略不计（或为零）。

• 没有漏磁通，即所有磁通都流过变压器的铁芯。

• 铁芯具有无限的磁导率，这意味着建立铁芯磁通所需的磁动势可以忽略不计。

• 没有由于绕组电阻、磁滞和涡流引起的损耗。因此，它的效率为100%。

理想变压器的原理

我们可以分析理想变压器在空载或负载下的工作情况，这将在以下部分进行讨论。

理想变压器空载工作

考虑一个空载的理想变压器，即其次级绕组开路，如图1所示。并且，初级绕组是一个纯电感线圈。

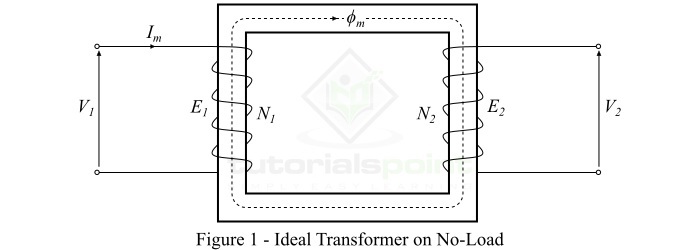
当一个交流电压$\mathit{V_{\mathrm{1}}}$施加到初级绕组时，它会吸取一个非常小的励磁电流$\mathit{I_{\mathit{m}}}$来建立铁芯中的磁通，该磁通滞后于施加电压90°。励磁电流Im在铁芯中产生一个与之成正比且同相位的交变磁通$\mathit{\phi_{m}}$。这个交变磁通($\mathit{\phi_{m}}$)通过磁耦合方式连接初级和次级绕组，并在初级绕组中感应出电动势$\mathit{E_{\mathrm{1}}}$，并在次级绕组中感应出电动势$\mathit{E_{\mathrm{2}}}$。

初级绕组中感应的电动势$\mathit{E_{\mathrm{1}}}$等于并与施加电压$\mathit{V_{\mathrm{1}}}$相反（根据楞次定律）。电动势$\mathit{E_{\mathrm{1}}}$和$\mathit{E_{\mathrm{2}}}$滞后于磁通($\mathit{\phi_{m}}$)90°，但是它们的幅值取决于初级和次级绕组的匝数。此外，电动势$\mathit{E_{\mathrm{1}}}$和$\mathit{E_{\mathrm{2}}}$彼此同相，而$\mathit{E_{\mathrm{1}}}$等于$\mathit{V_{\mathrm{1}}}$并与其反相180°。

理想变压器负载工作

当一个负载连接到理想变压器次级绕组的端子上时，则称变压器处于负载状态，负载电流流过次级绕组和负载。

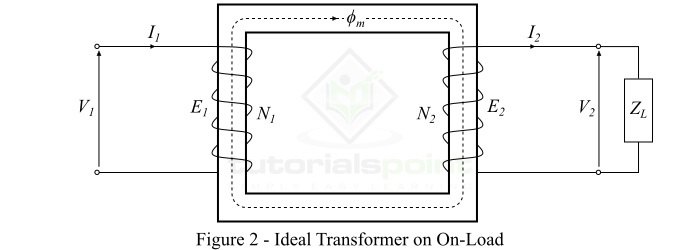
考虑一个阻抗为Z_L的感性负载连接到理想变压器的次级绕组上，如图2所示。然后，次级绕组电动势$\mathit{E_{\mathrm{2}}}$将导致电流$\mathit{I_{\mathrm{2}}}$流过次级绕组和负载，该电流由下式给出：

$$\mathrm{\mathit{I_{\mathrm{2}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}}$$

其中，对于理想变压器，次级绕组电动势$\mathit{E_{\mathrm{2}}}$等于次级绕组端电压$\mathit{V_{\mathrm{2}}}$。

由于我们考虑的是感性负载，因此，电流$\mathit{I_{\mathrm{2}}}$将滞后于$\mathit{E_{\mathrm{2}}}$或$\mathit{V_{\mathrm{2}}}$一个角度$\mathit{\phi_{\mathrm{2}}}$。此外，由于变压器是理想变压器，因此忽略空载电流$\mathit{I_{\mathrm{0}}}$。

流过次级绕组的电流($\mathit{I_{\mathrm{2}}}$)会建立一个磁动势($\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$)，该磁动势产生一个与主磁通($\mathit{\phi_{\mathit{m}}}$)方向相反的磁通$\mathit{\phi_{\mathrm{2}}}$。结果，铁芯中的总磁通量与其原始值发生变化，但是铁芯中的磁通量不应该偏离其原始值。因此，为了使铁芯中的磁通量保持其原始值，初级电流必须产生一个磁动势来抵消次级磁动势$\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$的退磁作用。

因此，初级电流$\mathit{I_{\mathrm{1}}}$必须流动，以便

$$\mathrm{\mathit{I_{\mathrm{1}}}\mathit{N_{\mathrm{1}}}\:=\:\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}}$$

因此，初级绕组必须吸取足够的电流来抵消次级电流的退磁作用，以使铁芯中的主磁通保持恒定。因此，当次级电流($\mathit{I_{\mathrm{2}}}$)增加时，初级电流($\mathit{I_{\mathrm{1}}}$)也以相同的方式增加，并使互磁通($\mathit{\phi_{\mathit{m}}}$)保持恒定。

在负载下的理想变压器中，次级电流$\mathit{I_{\mathrm{2}}}$滞后于次级端电压$\mathit{V_{\mathrm{2}}}$一个角度$\mathit{\phi _{\mathrm{2}}}$。

实际变压器

实际变压器具有以下特征：

• 初级和次级绕组具有有限的电阻。

• 存在漏磁通，即并非所有磁通都局限于铁芯。

• 铁芯具有有限的磁导率，因此需要相当数量的磁动势来建立铁芯磁通。

• 由于绕组电阻、磁滞和涡流，变压器中存在损耗。因此，实际变压器的效率始终小于100%。

典型实际变压器的分析模型如图3所示。

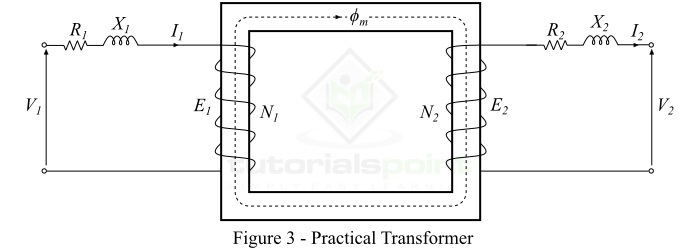
实际变压器的特性

以下是实际变压器的主要特性：

绕组电阻

变压器的绕组通常由铜导体组成。因此，初级和次级绕组都将具有绕组电阻，这会在变压器中产生铜损或$\mathit{i^{\mathrm{2}} \mathit{R}}$损耗。初级绕组电阻$\mathit{R_{\mathrm{1}}}$和次级绕组电阻$\mathit{R_{\mathrm{2}}}$分别与各自的绕组串联，如图3所示。

铁损或铁芯损耗

变压器的铁芯承受交变磁通，因此铁芯中会产生涡流损耗和磁滞损耗。磁滞损耗和涡流损耗统称为铁损或铁芯损耗。变压器的铁损取决于电源频率、铁芯中的最大磁通密度、铁芯体积和叠片厚度等。在实际变压器中，铁损的幅值实际上是恒定的且非常小。

漏磁通

初级绕组中的电流产生磁通。连接初级和次级绕组的磁通$\mathit{\phi _{\mathit{m}}}$是有用磁通，称为互磁通。但是，初级电流产生的部分磁通($\mathit{\phi _{\mathrm{1}}}$)不会与次级绕组连接。

当负载连接到次级绕组时，电流流过它并产生磁通($\mathit{\phi _{\mathrm{2}}}$)，该磁通仅与次级绕组连接。因此，$\mathit{\phi _{\mathrm{1}}}$的一部分和仅与其各自绕组连接的磁通$\mathit{\phi _{\mathrm{2}}}$称为漏磁通。

漏磁通的路径是空气，空气具有非常高的磁阻。因此，初级漏磁通($\mathit{\phi _{\mathrm{1}}}$)的作用是在初级绕组中引入一个与之串联的感抗($ \mathit{X_{\mathrm{1}}}$)。类似地，次级漏磁通($\mathit{\phi _{\mathrm{2}}}$)在次级绕组中引入一个与之串联的感抗($ \mathit{X_{\mathrm{2}}}$)，如图3所示。

但是，实际变压器中的漏磁通非常小（约占$\mathit{\phi _{m}}$的5%），但不能忽略。因为漏磁通路径是空气，空气具有非常高的磁阻。因此，它需要相当大的磁动势。

铁芯材料的有限磁导率

通常，实际变压器的铁芯由高等级硅钢制成，它具有特定的相对磁导率($\mathit{\mu _{r}}$)。因此，铁芯在某个磁通密度值下会饱和。因此，实际变压器的铁芯具有有限的磁导率，因此在磁通路径中具有磁阻。