变压器的电动势方程

---

---

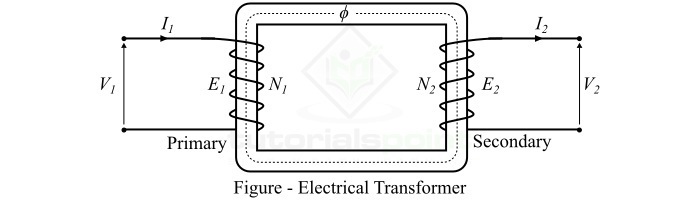
对于电力变压器，电动势方程是一个数学表达式，用于求解变压器绕组中感应电动势的大小。

考虑图中所示的变压器。如果N₁和N₂是初级和次级绕组的匝数。当我们在初级绕组上施加频率为f的交流电压V₁时，初级绕组会在铁心中产生交变磁通$\phi$。

如果我们假设正弦交流电压，则磁通可以表示为：

$$\mathrm{\mathit{\phi }\:=\:\phi _{m}\:\mathrm{sin}\:\mathit{\omega t}\:\cdot \cdot \cdot (1)}$$

现在，根据电磁感应原理，初级绕组中感应电动势e₁的瞬时值由下式给出：

$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$

$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\frac{\mathit{d}}{\mathit{dt}}\left ( \phi _{m}\: \mathrm{sin}\:\mathit{\omega t}\right )}$$

$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\:\mathit{\omega \phi \:cos\:\omega t}}$$

$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:-\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m} \:cos\:\omega t}}$$

其中：

$$\mathrm{\mathit{\omega \:=\:\mathrm{2}\pi f}}$$

$$\mathrm{\because -\mathit{cos\:\omega t}\:=\:\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )}$$

因此：

$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathrm{2}\mathit{\phi fN_{\mathrm{1}}}\:\mathit{\phi_{m}\:\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )}}\:\cdot \cdot \cdot (2)$$

方程 (2) 可以写成：

$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathit{E_{m_{\mathrm{1}}}}\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )\:\cdot \cdot \cdot (3)}$$

其中，$\mathit{E_{m_{\mathrm{1}}}}$ 是感应电动势 $\mathit{e_{\mathrm{1}}}$ 的最大值。

$$\mathrm{\mathit{E_{\mathrm{m1}}}\:=\:\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m}}}$$

现在，对于正弦电源，初级绕组电动势的有效值 $\mathit{E_{\mathrm{1}}}$ 由下式给出：

$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:\frac{\mathit{E_{m\mathrm{1}}}}{\sqrt{2}}\:=\:\frac{2\mathit{\pi fN_{\mathrm{1}}}\phi_{m}}{\sqrt{2}}}$$

$$\mathrm{\therefore\mathit{E_{\mathrm{1}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{1}}}\:\cdot \cdot \cdot (4)}$$

类似地，次级绕组电动势的有效值 E₂ 为：

$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{2}}}\:\cdot \cdot \cdot (5)}$$

一般地：

$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}N}\:\cdot \cdot \cdot (6)}$$

方程 (6) 称为变压器的电动势方程。

对于给定的变压器，如果我们将电动势方程除以电源频率，我们得到：

$$\mathrm{\frac{\mathit{E}}{\mathit{f}}\:=\:4.44\:\phi _{m}\mathit{N}\:=\:\mathrm{Constant}}$$

这意味着每单位频率的感应电动势是恒定的，但它在给定变压器的初级和次级侧并不相同。

此外，根据方程 (4) 和 (5)，我们有：

$$\mathrm{\frac{\mathit{E_{\mathrm{1}}}}{\mathit{E_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}\:or\:\frac{\mathit{E_{\mathrm{1}}}}{\mathit{N_{\mathrm{1}}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{N_{\mathrm{2}}}}}$$

因此，在变压器中，初级绕组每匝的感应电动势等于次级绕组每匝的感应电动势。

数值例子

一台单相 3300/240 V，50 Hz 变压器的铁心中最大磁通为 0.0315 Wb。计算初级和次级绕组的匝数。

解答

已知数据：

$$\mathrm{\mathit{E_{\mathrm{1}}\:=\:\mathrm{3300}\:\mathrm{V}\:\mathrm{and}\:\mathit{E_{\mathrm{2}}\:=\:\mathrm{240}\:V}}}$$

$$\mathrm{\mathit{f}\:=\:50\:Hz;\:\phi _{m}\:=\:0.0315\:Wb}$$

变压器的电动势方程为：

$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}N}}$$

因此，对于初级绕组：

$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:\frac{\mathit{E_{\mathrm{1}}}}{4.44\:\mathit{f\phi _{m}}}\:=\:\frac{3300}{4.44\times 50\times 0.0315}}$$

$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:471.9\:=\:472}$$

同样，对于次级绕组：

$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{4.44\:\mathit{f\phi _{m}}}\:=\:\frac{240}{4.44\times 50\times 0.0315}}$$

$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:34.32\:=\:35}$$

绕组不可能有部分匝数。因此，匝数必须是整数。