磁场中存储的能量

---

---

在上一章中，我们讨论了在机电能量转换装置中，电气系统和机械系统之间存在一个耦合介质。在大多数实际装置中，磁场用作耦合介质。因此，机电能量转换装置包括一个电磁系统。因此，存储在耦合介质中的能量以磁场的形式存在。我们可以计算如下所述的机电能量转换系统的磁场中存储的能量。

考虑一个线圈，该线圈具有N匝导线绕在磁芯上，如图 1 所示。该线圈由v伏电压源供电。

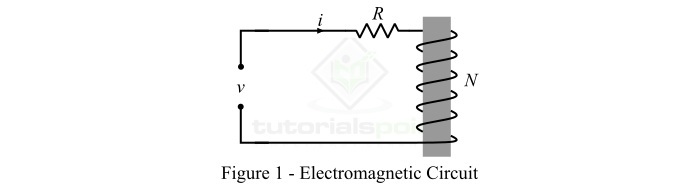
通过应用基尔霍夫电压定律，施加到线圈上的电压由下式给出：

$$\mathrm{\mathit{V\:=\:e\:+\:iR}\cdot \cdot \cdot (1)}$$

其中：

• e 是由于电磁感应而在线圈中感应出的电动势。

• R 是线圈电路的电阻。

• $\mathit{i}$ 是流过线圈的电流。

施加到电磁系统的瞬时功率由下式给出：

$$\mathrm{\mathit{p}\:=\:\mathit{Vi\:=\:i\left ( e+iR \right )}}$$

$$\mathrm{\Rightarrow \mathit{p}\:=\:\mathit{ie+ i^{\mathrm{2}}}\mathit{R}\cdot \cdot \cdot (2)}$$

现在，假设在时间t = 0 时，将直流电压施加到电路，并且在t = t₁ 秒结束时，电路中的电流已达到I 安培。然后，在此时间间隔内，输入系统的能量由下式给出：

$$\mathrm{\mathit{W}_{in}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{p\:dt}}$$

$$\mathrm{\Rightarrow \mathit{W}_{in}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{ie\:dt}\:+\:\int_{0}^{t_{\mathrm{1}}}\mathit{i^{\mathrm{2}}R\:dt}\cdot \cdot \cdot (3)}$$

从公式 3 可以看出，总输入能量由两部分组成：

• 第一部分是存储在磁场中的能量。

• 第二部分是由于线圈的电阻而产生的能量损耗。

因此，存储在系统磁场中的能量为：

$$\mathrm{\mathit{W}_{\mathit{f}}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{ie\:dt}\:\cdot \cdot \cdot (4)}$$

根据法拉第电磁感应定律，我们有：

$$\mathrm{\mathit{e}\:=\:\frac{\mathit{d\psi }}{\mathit{dt}}\:=\:\frac{\mathit{d}}{\mathit{dt}}\left ( \mathit{N\phi } \right )\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\cdot \cdot \cdot (5)}$$

其中，$\psi$ 是磁通链，等于$\mathit{\psi \:=\:N\phi }。

$$\mathrm{\therefore \mathit{W_{f}}\:=\:\int_{0}^{\mathit{t_{\mathrm{1}}}}\frac{\mathit{d\psi }}{\mathit{dt}}\mathit{i\:dt}}$$

$$\mathrm{\Rightarrow \mathit{W_{f}}\:=\:\int_{0}^{\psi_{\mathrm{1}}}\mathit{i\:d\psi }\cdot \cdot \cdot (6)}$$

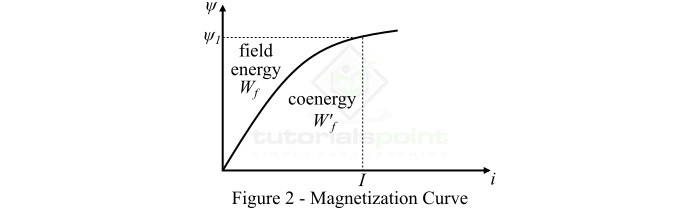
因此，公式 (6) 表明存储在磁场中的能量等于电磁系统（即磁化曲线）的 ($\psi -i$) 曲线与磁通链 ($\psi$) 轴之间的面积，如图 2 所示。

对于线性电磁系统，存储在磁场中的能量由下式给出：

$$\mathrm{\mathit{W_{f}}\:=\:\int_{0}^{\mathit{\psi _{\mathrm{1}}}}\mathit{id\psi }\:=\:\int_{0}^{\psi_{\mathrm{1}} }\frac{\psi }{\mathit{L}}\mathit{d\psi }}$$

其中，$\psi\:=\:\mathit{N\phi }\:=\:\mathit{Li}$，L 是线圈的自感。

$$\mathrm{\therefore \mathit{W_{f}}\:=\:\frac{\psi ^{\mathrm{2}}}{2\mathit{L}}\:=\:\frac{1}{2}\mathit{Li^{\mathrm{2}}}\cdot \cdot \cdot (7)}$$

余能的概念

余能是一个用于推导电磁系统中产生的转矩表达式的虚拟概念。因此，余能对系统没有物理意义。

基本上，余能是 $\psi -i$ 曲线与电流轴之间的面积，表示为 $\mathit{W_{f}^{'}}$，如上图 2 所示。

在数学上，余能由下式给出：

$$\mathrm{\mathit{W_{f}^{'}}\:=\:\int_{0}^{i}\psi \mathit{di}\:=\:\int_{0}^{i}\mathit{Li\:di}}$$

$$\mathrm{\Rightarrow \mathit{W_{f}^{'}}\:=\:\frac{1}{2}\mathit{Li^{\mathrm{2}}}\cdot \cdot \cdot (8)}$$

从公式 (7) 和 (8) 可以看出，对于线性磁系统，存储在磁场中的能量和余能相等。