数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学拉普拉斯变换和右侧及左侧信号的收敛域
什么是收敛域？
收敛域 (ROC) 定义为 s 平面上使函数 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$ 的拉普拉斯变换收敛的点集。换句话说，使函数 $\mathit{X}\mathrm{\left(\mathit{s}\right)}$ 收敛的 $\mathit{Re}\mathrm{\left(\mathit{s} \right)}$ (即 σ) 的范围称为收敛域。
右侧信号的ROC
如果信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$ 在 t < $\mathit{T}_{\mathrm{1}}$ 时为 0，其中 $\mathit{T}_{\mathrm{1}}$ 为某个有限时间（如图 1 所示），则称信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$ 为右侧信号。
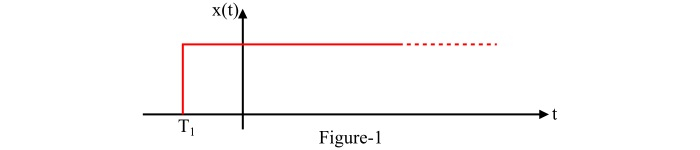
对于右侧信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$，拉普拉斯变换 $\mathit{X}\mathrm{\left(\mathit{s}\right)}$ 的 ROC 为 $\mathit{Re}\mathrm{\left(\mathit{s} \right )}>\mathrm{\sigma _{\mathrm{1}}}$，其中 $\mathrm{\sigma _{\mathrm{1}}}$ 为常数。因此，右侧信号的拉普拉斯变换的 ROC 在直线 $\sigma \mathrm{=} \mathrm{\sigma _{\mathrm{1}}}$ 的右侧。因果信号是右侧信号的一个例子。
数值例子 - 1
求右侧信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}\:\mathrm{=}\:2\mathit{e^{-\mathrm{4}t}u\mathrm{\left(\mathit{t}\right )}\:\mathrm{+}\:\mathrm{4}e^{-\mathrm{4}t}u\mathrm{\left (\mathit{t}\right)}}$ 的拉普拉斯变换和 ROC。
解答
给定信号为：
$$\mathrm{\mathit{x}\mathrm{\left(\mathit{t}\right)}\:\mathrm{=}\:2\mathit{e^{-\mathrm{4}t}\:u\mathrm{\left(\mathit{t}\right )}\:\mathrm{+}\:\mathrm{4}e^{-\mathrm{4}t}\:u\mathrm{\left (\mathit{t}\right)}}}$$
给定信号是右侧信号。实际上，它是一个因果信号。它的拉普拉斯变换由下式给出：
$$\mathrm{\mathit{L}\mathrm{\left[\mathit{x}\mathrm{\left(\mathit{t}\right)}\right]}\:\mathrm{=}\:2\mathit{L}\mathrm{\left[\mathit{e^{\mathrm{-4}t}\:u\mathrm{\left(\mathit{t}\right )}}\right]}\:\mathrm{+}\:4\mathit{L}\mathrm{\left[\mathit{e}^{\mathrm{-2}\mathit{t}}\:\mathit{u}\mathrm{\left (\mathit{t}\right)}\right]}}$$
$$\mathrm{\Rightarrow\:\mathit{X}\mathrm{\left(\mathit{s}\right)}\:\mathrm{=}\:\mathrm{\left(\frac{2}{\mathit{s}+\mathrm{4}}\right)}\mathrm{+}\mathrm{\left(\frac{4}{\mathit{s}+\mathrm{2}}\right)};\:\mathrm{ROC}\to \mathit{Re\mathrm{\left(\mathit{s}\right)}}>-4\:\mathrm{and}\:\mathit{Re\mathrm{\left(\mathit{s}\right)}}>-2}$$
因此，给定右侧信号的 ROC 为：
$$\mathrm{\mathrm{\left[\mathit{Re\mathrm{\left(\mathit{s}\right)}}>-4\:\cap \:\mathit{Re\mathrm{\left(\mathit{s}\right)}}>-2 \right ]}\:\mathrm{=}\:\mathit{Re\mathrm{\left(\mathit{s}\right)}}>-2}$$
$$\mathrm{\Rightarrow \mathrm{ROC\to }\mathit{Re\mathrm{\left(\mathit{s}\right)}}>-2}$$
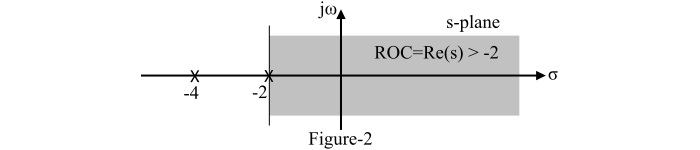
给定信号的拉普拉斯变换的 ROC 如图 2 所示。需要注意的是，ROC 延伸到最右极点的右侧，并且 ROC 内不存在极点。
左侧信号的ROC
如果信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$ 在 t > $\mathit{T}_{\mathrm{2}}$ 时为 0，其中 $\mathit{T}_{\mathrm{2}}$ 为某个有限时间（如图 3 所示），则称信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$ 为左侧信号。
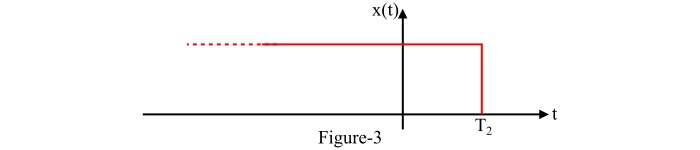
对于左侧信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$，拉普拉斯变换 $\mathit{X}\mathrm{\left(\mathit{s}\right)}$ 的 ROC 为 $\mathit{Re}\mathrm{\left(\mathit{s}\right)}<\mathrm{\sigma _{\mathrm{2}}}$，其中 $\mathrm{\sigma _{\mathrm{2}}}$ 为常数。因此，左侧信号的拉普拉斯变换的 ROC 在直线 $\sigma \mathrm{=}\mathrm{\sigma _{\mathrm{2}}}$ 的左侧。反因果信号是左侧信号的一个例子。
数值例子 - 2
求左侧信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}\:\mathrm{=}\:\mathit{e^{\mathrm{2}t}\:u\mathrm{\left(\mathit{-t}\right )}\:\mathrm{+}\:\mathrm{3}e^{\mathrm{5}t}\:u\mathrm{\left (\mathit{-t}\right)}}$ 的拉普拉斯变换和 ROC。
解答
给定信号为：
$$\mathrm{\mathit{x}\mathrm{\left(\mathit{t}\right)}\:\mathrm{=}\:\mathit{e^{\mathrm{2}t}\:u\mathrm{\left(\mathit{-t}\right )}\:\mathrm{+}\:\mathrm{3}\mathit{e}^{\mathrm{5}\mathit{t}}\:\mathit{u}\mathrm{\left (\mathit{-t}\right)}}}$$
由于给定信号是左侧信号，因此它是一个反因果信号。信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$ 的拉普拉斯变换由下式给出：
$$\mathrm{\mathit{L}\mathrm{\left[\mathit{x}\mathrm{\left(\mathit{t}\right)}\right]}\:\mathrm{=}\:\mathit{L}\mathrm{\left[\mathit{e^{\mathrm{2}t}\:u\mathrm{\left(\mathit{-t}\right )}}\right]}\mathrm{+}3\mathit{L}\mathrm{\left[\mathit{e}^{\mathrm{5}\mathit{t}}\:\mathit{u}\mathrm{\left (\mathit{-t}\right)}\right]}}$$
$$\mathrm{\Rightarrow\:\mathit{X}\mathrm{\left(\mathit{s}\right)}\mathrm{=}\:-\frac{1}{\mathit{s}-\mathrm{2}}-\frac{3}{\mathit{s}-\mathrm{5}};\:\mathrm{ROC}\to \mathit{Re\mathrm{\left(\mathit{s}\right)}}<2\:\mathrm{and}\:\mathit{Re\mathrm{\left(\mathit{s}\right)}}<5}$$
因此，给定左侧信号的拉普拉斯变换的 ROC 为：
$$\mathrm{\mathrm{\left[\mathit{Re\mathrm{\left(\mathit{s}\right)}}<2\:\cap \:\mathit{Re\mathrm{\left(\mathit{s}\right)}}<5 \right ]}\:\mathrm{=}\:\mathit{Re\mathrm{\left(\mathit{s}\right)}}<2}$$
$$\mathrm{\Rightarrow \mathrm{ROC\to }\mathit{Re\mathrm{\left(\mathit{s}\right)}}<2}$$
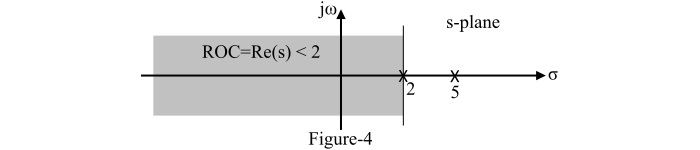
左侧信号 $\mathit{x}\mathrm{\left(\mathit{t}\right)}$ 的 ROC 如图 4 所示。需要注意的是，ROC 延伸到最左极点的左侧，并且 ROC 内不存在极点。
浏览量 10K+
