数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学一根 5 米长的梯子靠在一面竖直的墙上，梯子顶端距离地面 4 米。如果梯子的底部向墙移动 1.6 米，求梯子顶端沿墙向上滑动的距离。
已知：一根 5 米长的梯子靠在一面竖直的墙上，梯子顶端距离地面 4 米。如果梯子的底部向墙移动 1.6 米
求解：梯子顶端沿墙向上滑动的距离。
解题步骤
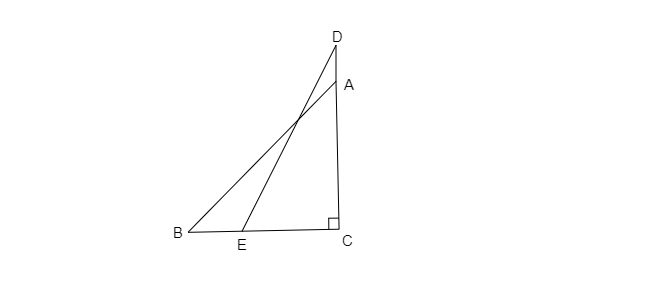
已知，梯子长度=斜边 AB=5 米
底边 BC=?
墙的高度=高 AC=4 米
在直角三角形 ABC 中，根据勾股定理
底边²=斜边²-高²
⇒ BC²=5²-4²
⇒ BC²=25-16
⇒ BC=√9
⇒ BC=3 米
当底边缩短 1.6 米时
底边 EC=BC-BE=3-1.6=1.4 米
斜边=梯子高度 DE=5 米
高 DC=?
高²=斜边²-底边²
⇒ DC²=5²-1.4²
⇒ DC²=25-1.96
⇒ DC=√23.04
⇒ DC=4.8 米
∴梯子顶端沿墙向上滑动的距离=DA=DC-AC=4.8-4=0.8 米
更新于：2022年10月10日
94 次浏览
广告