一个梯子斜靠在墙上，仰角为\( 60^{\circ} \)，梯脚距墙\( 9.5 \mathrm{~m} \)。求梯子的长度。

已知

一个梯子斜靠在墙上，仰角为\( 60^{\circ} \)，梯脚距墙\( 9.5 \mathrm{~m} \)。

要求

我们需要求出梯子的长度。

解：  

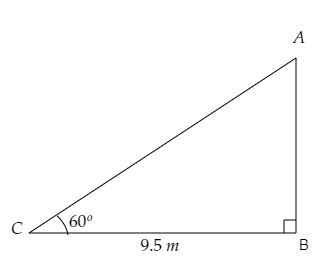
设AB为墙，AC为梯子。

梯脚（C点）距墙\( 9.5 \mathrm{~m} \)。

由图可知：

$\mathrm{BC}=9.5 \mathrm{~m}, \angle \mathrm{ACB}=60^{\circ}$

设梯子长度为$\mathrm{AC}=h \mathrm{~m}$

我们知道：

$\cos \theta=\frac{\text { 底边 }}{\text { 斜边 }}$

$=\frac{\text { BC }}{AC}$

$\Rightarrow \cos 60^{\circ}=\frac{9.5}{h}$

$\Rightarrow \frac{1}{2}=\frac{9.5}{h}$

$\Rightarrow h=9.5 \times 2 \mathrm{~m}$

$\Rightarrow h=19 \mathrm{~m}$

因此，梯子的长度为 $19 \mathrm{~m}$。 

更新于：2022年10月10日

浏览量：113

开启你的职业生涯

完成课程获得认证

开始学习
广告