Loading [MathJax]/jax/element/mml/optable/Latin1Supplement.js

一个牛奶容器由金属板制成，形状为圆台，体积为 $\displaystyle 10459\frac{3}{7} \ cm^{3}$ 。其上下底圆的半径分别为 $\displaystyle \ 8$ cm和 $\displaystyle 20$ cm。求制作该容器所用金属板的成本，金属板价格为每平方厘米1.40卢比。

学术数学 NCERT 10年级

已知：容器体积

$( V)=10459\frac{3}{7}$ ，上底圆半径

$( r)=8\ cm$ ，下底圆半径

$( R)=20\ cm$ ，金属板成本=每平方厘米1.40卢比。

求解：求制作该容器所需金属板的总成本。

解答

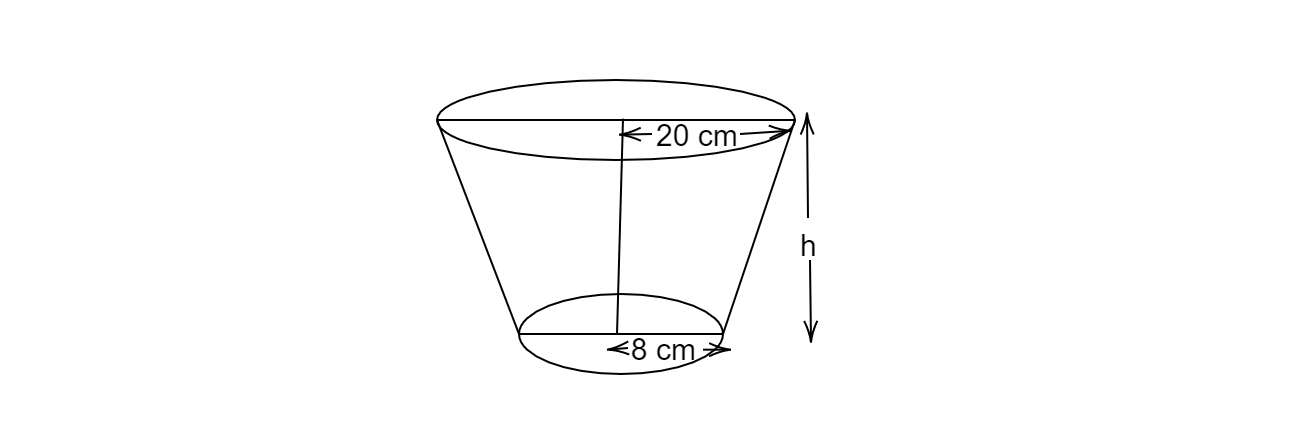
下底半径

$r=8\ cm$

上底半径

$R=20\ cm$

设圆台高度为

$h\ cm$ 。

则圆台体积 V

$=\frac{\pi }{3} h\left( R^{2} +r^{2} +Rr\right)$

$=\frac{\pi}{3}\ h\left(( 20)^{2} +( 8)^{2} +20\times 8\right)$

$=\frac{22}{7} \times \frac{1}{3} \times 624\times h$

$=\frac{22}{7} \times h\times 208$

已知体积 V

$=10459\frac{3}{7}$

代入其值，

$\frac{73216}{7} =\frac{22}{7} \times h\times 208$

$\Rightarrow h=\frac{73216}{22\times 208}$

$\Rightarrow h=16\ cm$

容器的总表面积 A

$=\pi( R+r)\sqrt{\left(( R-r)^{2} +h^{2} \ \right)} +πr^{2}$

$=\ \ \frac{22}{7}( 20+8)\sqrt{\left(( 20-8)^{2} +( 16)^{2} \ \right)} +\frac{22}{7} \times 8\times 8$

$=\frac{22}{7}( 28)\sqrt{\left(( 12)^{2} +( 16)^{2} \ \right)} +\frac{22}{7} \times 8\times 8$

$=\frac{22}{7}\left( 28\sqrt{( 144+256)} +64\right)$

$=\frac{22}{7}\left( 28\times \sqrt{400} +64\right)$

$=\frac{22}{7}( 28\times 20+64)$

$=\frac{22}{7} \times 624$

已知金属成本为每平方厘米1.40卢比。

金属总成本

$=表面积\times 1.40$

$=\frac{22}{7} \times 624\times 1.40$

$=2745.60$ .

因此，制作该容器的金属板成本为2745.60卢比。

Tutorialspoint

更新于：2022年10月10日

浏览量：56

开启你的职业生涯

完成课程获得认证

广告