一个顶部开口的桶，由金属片制成，形状为圆台。桶的深度为 24 厘米，其上、下圆形底端的直径分别为 30 厘米和 10 厘米。如果每 100 平方厘米金属片的成本为 10 卢比，求制作该桶所需金属片的成本。[使用 π = 3.14]。

已知：一个圆台形状的桶，深度为 24 厘米，其上、下圆形底端的直径分别为 30 厘米和 10 厘米。金属片的单价为 10 卢比/100平方厘米。

求解：求制作该圆台所需金属片的成本。

解答

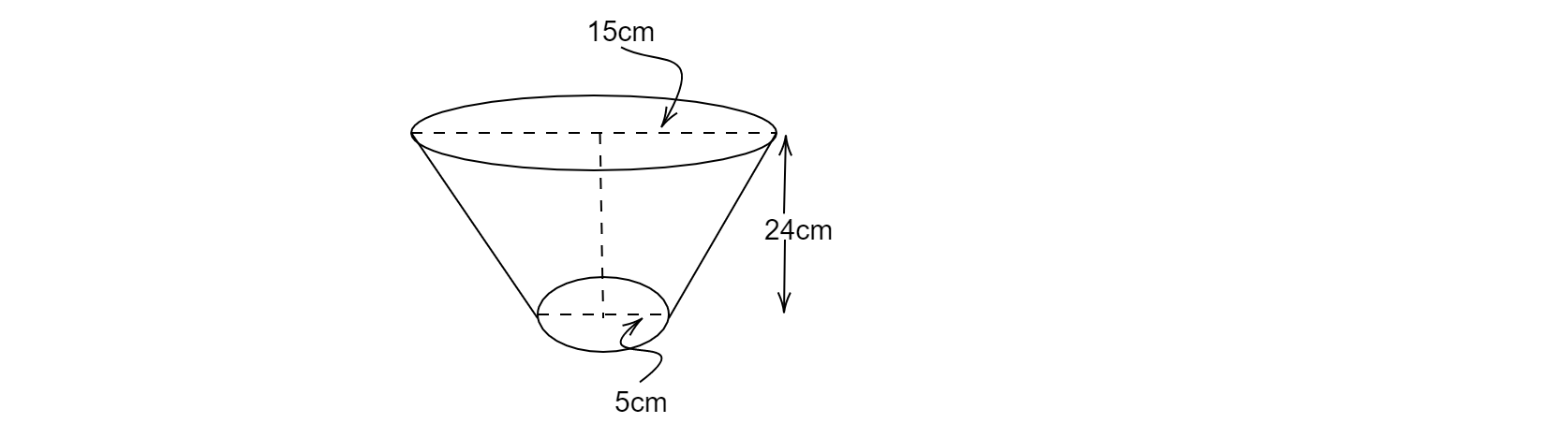
桶上端直径，$d_{1} = 30$ 厘米

桶上端半径 $(r_{1}) = \frac{d_{1}}{2}$

$= \frac{30}{2}$

$= 15$ 厘米

桶下端直径 $d_{2} = 10$ 厘米

桶下端半径 $(r_{2}) = \frac{d_{2}}{2}$

$= \frac{10}{2}$

$= 5$ 厘米

圆台的母线长度 $(l) = \sqrt{(r_{1} - r_{2})^{2} + h^{2}}$

$= \sqrt{(15 - 5)^{2} + 24^{2}}$

$= \sqrt{100 + 576}$

$= \sqrt{676}$

$= 26$ 厘米

制作水桶所需的金属片面积 = 圆台侧面积 + 底面积

$= \pi (r_{1} + r_{2})l + \pi r_{2}^{2}$

$= \pi [(15 + 5) \times 26 + 5^{2}]$

$= \pi [(20 \times 26) + 25]$

$= 545\pi$ 平方厘米

100 平方厘米金属片的成本 = 10 卢比

$545\pi$ 平方厘米金属片的成本 $= \frac{545 \times 3.14 \times 10}{100}$

= 171.13 卢比

因此，制作该桶所需金属片的成本为 171.13 卢比。
 

更新于：2022年10月10日

浏览量：116

开启你的职业生涯

完成课程获得认证

开始学习
广告