一个木制玩具是由一个实心圆柱体两端挖去半径相同的半球制成的。如果圆柱体的高度为 10 厘米，底面半径为 3.5 厘米，求玩具的木料体积。[使用 $\pi =\frac{22}{7}$]。

已知：实心圆柱体的高度 $=10\ cm$，底面半径 $=3.5\ cm$

要求：求由给定圆柱体两端挖去半径相同的半球制成的玩具的木料体积。

解答

圆柱体的高度，$h=10\ cm$

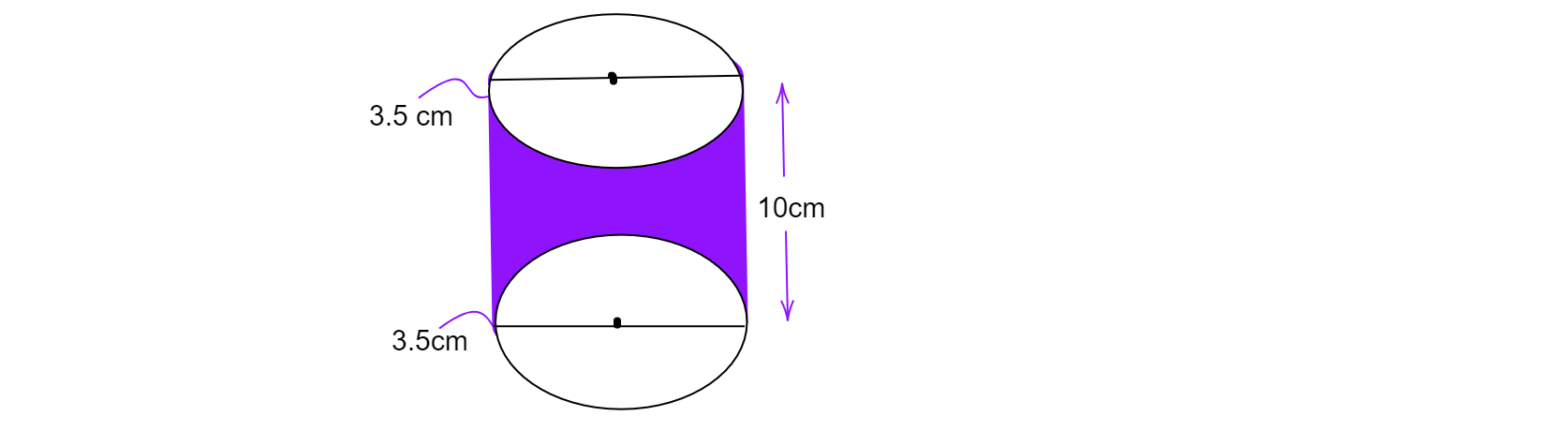
圆柱体的半径 = 每个半球的半径，$r=3.5\ cm$

每个半球的体积$=\frac{2}{3} \pi r^{3}$

圆柱体的体积 $=\pi r^{2} h$

$\therefore$ 玩具的木料体积$=$圆柱体的体积 $-2\times$ 每个半球的体积

$=\pi r^{2} h-2\times \frac{2}{3} \pi r^{3}$

$=\pi r^{2}\left( h-2\times \frac{2}{3} r\right)$

$=\frac{22}{7} \times 3.5\times 3.5( 10-2\times \frac{2}{3} \times 3.5)$

$=38.5\times 5.33$

$=205.205\ cm^{3} $

因此，玩具的木料体积为 $205.205\ cm^{3}$。

更新于： 2022年10月10日

2K+ 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告

© . All rights reserved.