数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究PQ是一根已知高度为a的柱子，AB是一座位于一定距离处的塔。如果α和β分别是P点和Q点测得塔顶B的仰角，求塔的高度及其与柱子的距离。
已知
PQ是一根已知高度为a的柱子，AB是一座位于一定距离处的塔。α和β分别是P点和Q点测得塔顶B的仰角。
要求
我们需要求出塔的高度及其与柱子的距离。
解法
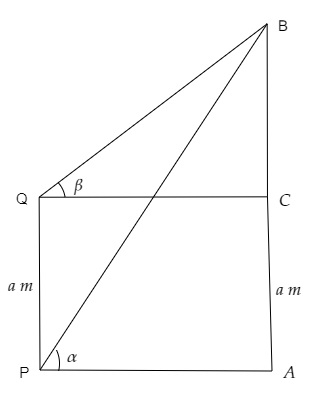
PQ是柱子，AB是塔。
从P点和Q点测得B点的仰角分别为α和β。
PQ=a
设AB=h，塔与柱子之间的距离为PA=x米。
AC=a，BC=h-a
在△BPA中，
tan α=BA/PA
=h/x
x tan α=h.............(i)
同样地，
在△BQC中，
tan β=BC/QC
= (h-a)/x
=> x tan β=h-a
=> x tan β=x tan α-a [根据(i)]
=> x tan α-x tan β=a
=> x(tan α-tan β)=a
=> x=a/(tan α-tan β)
=> h=x tan α=[a/(tan α-tan β)] × tan α
= [a tan α]/(tan α-tan β)
因此，塔的高度为[a tan α]/(tan α-tan β)，塔与柱子之间的距离为a/(tan α-tan β)。
更新于：2022年10月10日
浏览量：83
广告