指出下列各点的像的坐标。
(i) \( P(5,8), Q(-7,11), R(10,-6), T(-15,-7) \) 在x轴上反射后的像
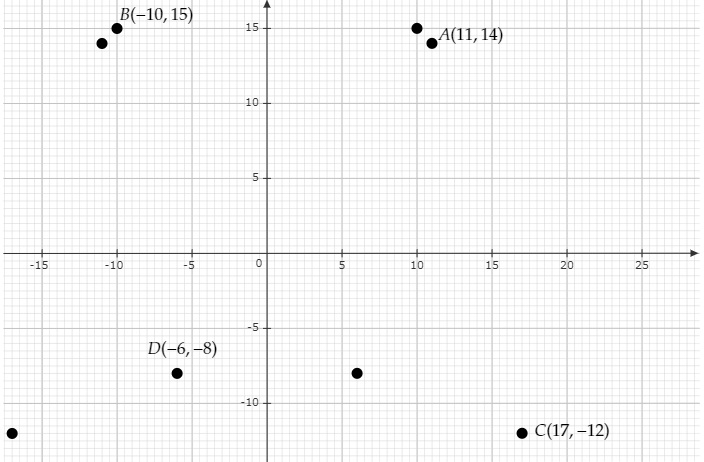
(ii) \( A(11,14), B(-10,15), C(17,-12), D(-6,-8) \) 在\( y \)轴上反射后的像。将所有上述点及其像分别绘制在不同的网格上。

(i) 点 $(a, b)$ 在x轴上的像是 $(a, -b)$

因此，

$P(5, 8)$ 在x轴上反射后的像是 $(5, -8)$。

$Q(-7, 11)$ 在x轴上反射后的像是 $(-7, -11)$。

$R(10, -6)$ 在x轴上反射后的像是 $(10, -(-6))=(10, 6)$。

$S(-15, -7)$ 在x轴上反射后的像是 $(-15, -(-7))=(-15, 7)$。

(ii) 点 $(a, b)$ 在y轴上的像是 $(-a, b)$

因此，

$A(11, 14)$ 在y轴上反射后的像是 $(-11, 14)$。

$B(-10, 15)$ 在y轴上反射后的像是 $(-(-10), 15)=(10, 15)$。

$C(17, -12)$ 在y轴上反射后的像是 $(-17, -12)$。

$D(-6, -8)$ 在y轴上反射后的像是 $(-(-6), -8)=(6, -8)$。

教程点

更新于: 2022年10月10日

100 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习